一文带你搞定二分(真的详细，建议收藏)

Posted 2021-09-04 追道者

二分，相信对于大多数初涉算法的同学来说，真的是玄学编程。主体思想容易至极，可是细节处理，边界处理，真的是无比难受。本文结合笔者踩过的坑，意图带大家搞清二分的本质。
二分法通常有四种常见类型，我们逐一来看。若想速查，可直接看最后总结。
说明: int mid = left + (right-left) / 2; 等价于 int mid = (left + right) / 2; 只是后者在算法比赛中 left + right 可能会超出整形范围导致结果出错，建议使用前一种形式，后文不在解释。

一.寻找唯一值

这种二分是整数二分中最基本的一种，我们以力扣35. 搜索插入位置为例进行讲解。
题目为:

二分的前提是必须是有序数组，本质思想为取中进行条件判断，每次根据判定结果将搜索区间减少一半，最终确定目标值。
下面附上代码，请读者一定要注意标明的坑点:

int searchInsert(int* nums, int numsSize, int target)
{
    int left = 0;
    int right = numsSize - 1;	//坑点1
    while (left <= right) {		//坑点2
        int mid = left + (right-left) / 2;
        if (nums[mid] == target) {
            return mid;		//找到该数，返回
        }
        //坑点3
        else if (nums[mid] < target) {
            left = mid + 1;
        }
        else {
            right = mid - 1;
        }
    }
    //未找到时根据题目要求进行处理，这部分要根据题意，就不带大家分析了~
    if (left >= numsSize) {
        return numsSize;
    }
    return nums[left]<target ? right : left;
}

1.右边界定义

这种情况下，要求我们搜素一个数字，我们定义二分右边界为数组末尾元素下标（数组长度-1），如此我们的搜索区间为 [left, right]，右边为闭区间。这种情况下，如此定义是比较简单的。

2.循环终止条件

看循环终止条件首先就得看我们的搜索区间 [left,right]，为闭区间，也就是说，当 left == right 时我们的搜索区间里还有一个数left或者right未经判断，所以这时还得进入循环，判断这个数是不是满足条件。
当然，我们知道原因后，也可以写成 <不过循环退出后，我们要对left或者right这个数特殊判断一下。下文统一使用 left:

while (left < right) {
	.....
}
if (nums[left] == target) {
	return left;
}
// 未找到，根据题目要求处理。

3.条件更新

这里就很迷惑了，很多时候我们可以看到 left = mid, left = mid + 1, right = mid, right = mid + 1,到底该如何选择？
针对这种情况，我们思考，当我们要进行条件更新意味着什么？意味着我们现在的 mid 并不满足条件。而我们的搜索区间为闭区间，所以我们要将 mid 在接下来的搜索中排除，即将搜索区间更新为 [left, mid-1] 或者 [mid+1, right]。这样我们的条件更新自然就是：

left = mid + 1;
right = mid - 1;

二.寻找左边界

这种情况是上一种二分的进阶，要求是在一排序好的数组里，查找满足某一性质的值的最小下标，我们仍以力扣 34. 在排序数组中查找元素的第一个和最后一个位置进行解析。（这题使用C++ vector容器，本质就是数组）
题目如下：

这道题目要求查找左右边界，我们先看左边界查找，还是一样，注意坑点：

    int LeftSearch(vector<int>& nums, int target)
    {
        int left = 0;
        int right = nums.size();	//坑点1
        while (left < right) {		//坑点2
            int mid = left + (right-left) / 2;
            //坑点3
            if (nums[mid] >= target) {
                right = mid;
            }
            else {   // nums[mid] < target
                left = mid + 1;
            }
        }
        //未找到处理，坑点4!
        if (left == nums.size()) {
            return -1;
        }
        return nums[left]==target ? left : -1;
    }

1.右边界定义

这里要求我们搜素一个范围的左边界，我们定义右边界为数组长度（数组末尾元素下标+1），这就意味着我们的搜索区间为 [left, right) 为左闭右开区间。

2.循环终止条件判断

同样的，看循环终止条件就得看搜索区间，我们的搜索区间为 [left, right) 左闭右开，当 left == right 时，[left, left) 区间已经是空区间，无需再次进入循环进行判断。

3.条件更新

这里也是最难理解的一点。
首先，我们得想两个问题：

①循环终止条件？

答：当 left == right 循环退出。

②如果存在答案，答案保存在哪里？(重要)

这里，我们得理解，像第一种情况，找一个确定的数字，我们只要找到了就可以直接break退出循环。但下面这两种情况，我们如果找到了一个满足条件的数，是不能直接退出循环的，因为我们要找的是这组数的边界！所以我们只能退出循环时，将我们的答案卡在区间里。所以，循环结束后，left 或right就是我们的答案！

所以，当 nums[mid] >= target 时，我们的 mid 肯定是左边界，或者左边界的右侧，这时，我们只能令 right = mid，如果令 right = mid - 1，当mid就是左边界时，我们就完美的避开了答案。
同理，当 nums[mid] < target 时，mid 一定在左边界的左侧，此时，我们就要让 left = mid + 1，查找mid 的右侧区域。
这里，请不要疑惑，为什么将等号放在 nums[mid] >= target 而不放在 <= 那里。因为我们查找左边界，本质上可以理解为，查找一排序数组中大于等于target的最小下标。而你不能理解为，小于等于target的最大下标，因为那样找出来的是右边界！

4.额外判断

一句话：我们查找左边界，本质上可以理解为，查找一排序数组中大于等于target的最小下标，所以，严格来说，我们找到的那个值的大于等于target的，所以我们得判断，这个值是不是target，若不是，说明数组中压根不存在target，我们返回-1。
还有一种情况是 target 大于数组最后一个元素，这种情况下 left 会一直更新到 right 的位置，造成越界，我们得特殊判断一下。

三.寻找右边界

右边界查找与左边界比较相似，还是上题，我们附上代码：

    int RightSearch(vector<int>& nums, int target)
    {
        int left = 0;
        int right = nums.size(); //坑点1
        while (left < right) {   //坑点2
            int mid = left + (right - left) / 2;
            //坑点3
            if (nums[mid] <= target) {
                left = mid + 1;
            }
            else {
                right = mid;
            }
        }
        //坑点4
        if (left - 1 >= nums.size() || left - 1 < 0) {
            return -1;
        }
        if (nums[left-1] != target) {
            return -1;
        }
        return left - 1;
    }

1. 右边界定义 & 循环条件判断

这里我们的要求依旧是找一组数的边界，所以我们仍然将右边界定义为数组长度，循环条件为 left < right，与左边界处理情况相同。

2. 条件更新

寻找右边界，可以理解为查找小于等于target的最大下标。
那么，按照左边界的理解，我们似乎应该将条件更新写成这样：

    if (nums[mid] <= target) {
        left = mid;
    }
    else {
        right = mid - 1;
    }

这样写似乎顺理成章，nums[mid] <= target 时，右边界在mid或mid的右侧，所以我们令 left = mid，反之，right = mid - 1，可是，如果这样写，会有一个致命的问题：
看这样一个测试用例：

nums[] = {1};
target = 1;

初始化，left = 0， right = nums.size() = 1; 进入循环，mid = (left + right) / 2 = 1 / 2 = 0;
nums[mid] <= target, left = mid = 0; 这里问题就出现了，一次循环过后 left 和 right 都没有得到更新，所以就会造成死循环!
故我们可以得出结论：由于整除的特殊性质，为避免死循环情况的出现，我们进行整数二分条件更新时，一定不能直接写 left = mid ！！
所以，我们只能写成这样：

     if (nums[mid] <= target) {
         left = mid + 1;
     }
     else {
         right = mid;
     }

4. 额外判断

请思考一个问题，这种情况下，我们跳出循环后，如果存在答案，保存在哪里？

     if (nums[mid] <= target) {
         left = mid + 1;
     }

我们思考，当此时的 mid 就是我们寻找的右边界时，我们令 left = mid + 1，也就是说，这种情况下，我们的右边界保存在 left - 1 里!!
如此，我们的判断部分就很好理解了，首先，我们判断 left - 1 这个下标是否合法:

        if (left - 1 >= nums.size() || left - 1 < 0) {
            return -1;
        }

然后判断 nums[left-1] 这个数是不是我们要找的 target：

        if (nums[left-1] != target) {
            return -1;
        }

如果都没问题，就可以返回 left - 1 了。

附：如果实在不理解为什么要加这么多判断，可以把它们选择性省略，然后到力扣提交，就可以看到对应的测试用例了~

四.浮点数二分

浮点数二分可谓是最为简单的二分类型，几乎都不要考虑边界条件，我们直接以AcWing上的一道模板题为例: 790.数的三次方根
题目如下：

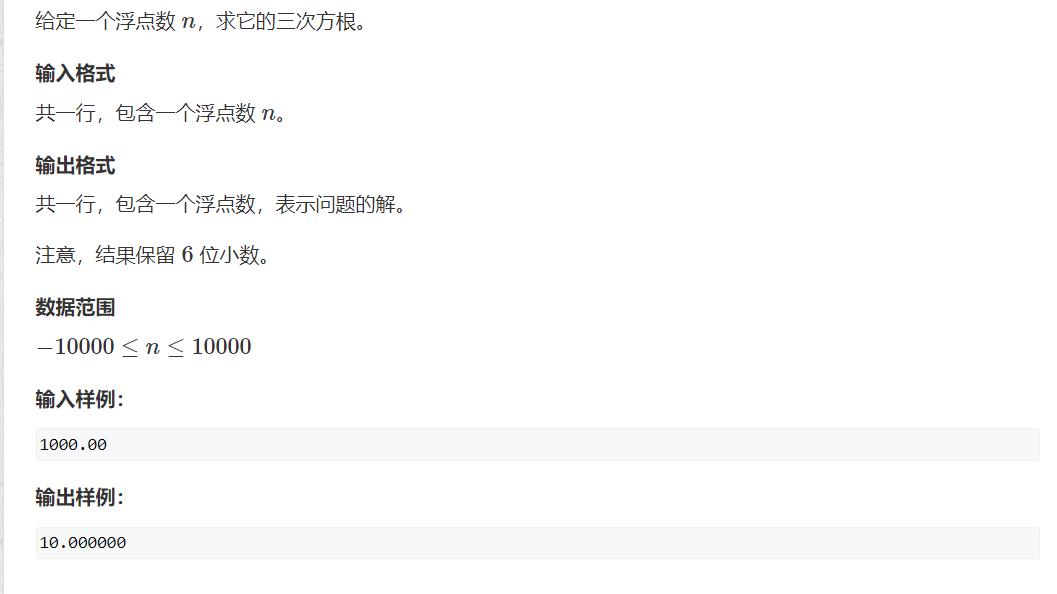
写浮点数二分，最主要的是注意它的数据范围，附上代码：

#include <iostream>

using namespace std;

int main()
{
	double x;
	cin >> x;

	double left = -10000;
	double right = 10000;

	while (right - left > 1e-8) {
		double mid = (left + right) / 2;
		if (mid*mid*mid > x)
			right = mid;
		else
			left = mid;
	}
	printf("%.6lf", left);
	
	return 0;
}

我们可以直接以题目所给的数据范围作为左右边界，这样便无需考虑一些特殊情况（如0-1的数开方比原数大）。
浮点数二分我们需要定义一个精度，一般定义的精度比题目要求的精度多两个小数点最为保险。
当 left 和 right 之间的距离小于这个精度时，我们就认为这个区间里任意一个数都可以作为答案，此时跳出循环，直接输出 left 就好了。
注：新手在写的时候要注意，浮点二分所有的数据类型都是 double 可不要一个手滑写成 int，完了出错还傻傻的半天还找不出来。(呜呜呜~)

五. 整数二分总结

浮点数二分较为简单，我们总结一下整数二分。

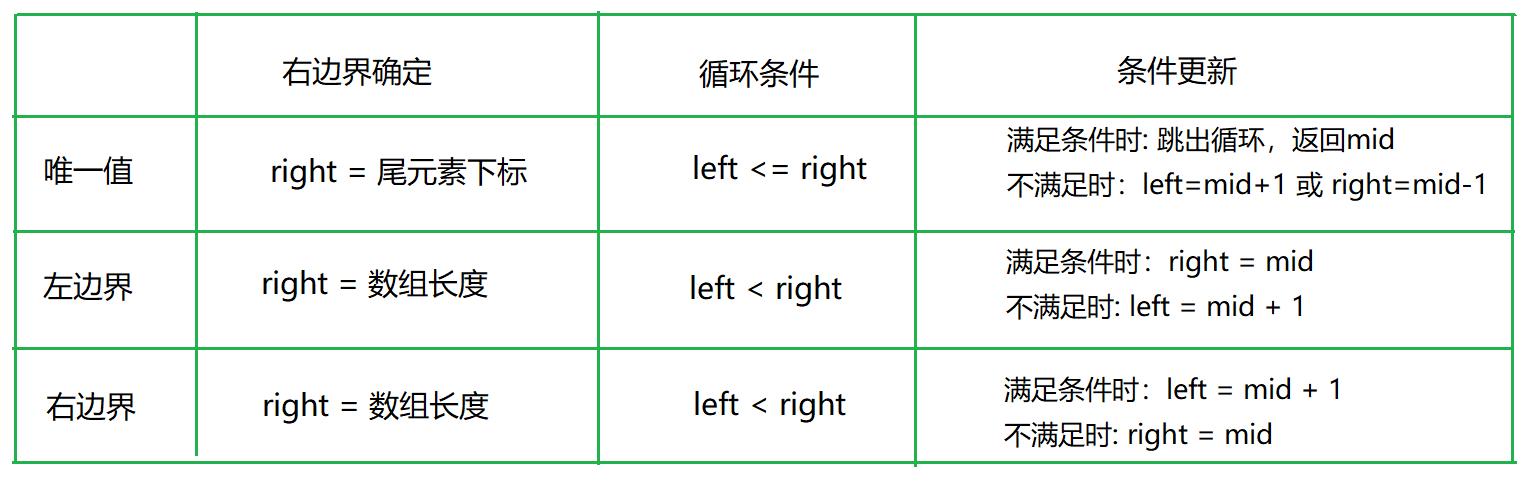
特别注意，寻找右边界时，返回的答案是保存在 left - 1 里的!!