倍增选做-

Posted 2021-09-04 Harris-H

倍增选做

P1707 刷题比赛

构造一个$11\times 11$​ 矩阵，然后快速幂即可。

代码参考题解区

#include <cstdio>
#include <iostream>
#include <cstring>

using namespace std;

typedef long long ll;

ll m, p, q, r, t, u, v, w, x, y, z;

struct Matrix {
	int n, m;
	ll a[15][15];
	
	inline Matrix () {
		memset(a, 0, sizeof(a));
	}
} base, ans;

inline ll quickMul (ll a, ll b) {
	ll res = 0;
	a %= m;
	b %= m;
	while (b) {
		if (b & 1)
			res = (res + a) % m;
		b >>= 1;
		a = (a + a) % m;
	}
	return res;
}

inline Matrix operator * (Matrix a, Matrix b) {
	Matrix res;
	res.n = a.n;
	res.m = b.m;
	for (int i = 1; i <= a.n; i++)
		for (int j = 1; j <= b.m; j++)
			for (int k = 1; k <= a.m; k++)
				res.a[i][j] = (res.a[i][j] + quickMul(a.a[i][k], b.a[k][j])) % m;
	return res;
}

inline Matrix quickPow (Matrix a, ll k) {
	Matrix res;
	res.n = res.m = a.n;
	for (int i = 1; i <= a.n; i++)
		res.a[i][i] = 1;
	while (k) {
		if (k & 1)
			res = res * a;
		k >>= 1;
		a = a * a;
	}
	return res;
}

inline void init_base () {
	base.n = base.m = 11;
	base.a[1][2] = base.a[1][3] = base.a[1][4] = base.a[2][1] = base.a[2][3] = base.a[2][5] = base.a[3][1] = base.a[3][2] = base.a[3][6] = base.a[7][7] = base.a[8][3] = base.a[8][8] = base.a[9][1] = base.a[9][7] = base.a[9][8] = base.a[9][9] = base.a[10][2] = base.a[11][3] = 1;
	base.a[8][7] = base.a[9][3] = 2;
	base.a[1][1] = p;
	base.a[2][2] = u;
	base.a[3][3] = x;
	base.a[4][1] = q;
	base.a[5][2] = v;
	base.a[6][3] = y;
	base.a[7][1] = r;
	base.a[8][1] = t;
	base.a[10][10] = w;
	base.a[11][11] = z;
}

inline void init_ans () {
	ans.n = 1;
	ans.m = 11;
	ans.a[1][1] = ans.a[1][2] = ans.a[1][3] = 3;
	ans.a[1][4] = ans.a[1][5] = ans.a[1][6] = ans.a[1][7] = ans.a[1][8] = ans.a[1][9] = 1;
	ans.a[1][10] = w;
	ans.a[1][11] = z;
}

int main () {
	ll n;
	scanf("%lld %lld %lld %lld %lld %lld %lld %lld %lld %lld %lld %lld", &n, &m, &p, &q, &r, &t, &u, &v, &w, &x, &y, &z);
	if (n < 2) {
		puts("nodgd 1");
		puts("Ciocio 1");
		puts("Nicole 1");
		return 0;
	}
	init_base();
	init_ans();
	ans = ans * quickPow(base, n - 2);
	printf("nodgd %lld\\nCiocio %lld\\nNicole %lld", ans.a[1][1], ans.a[1][2], ans.a[1][3]);
	return 0;
}

P6648 [CCC 2019] Triangle: The Data Structure

毒瘤倍增，考虑维护正三角和倒三角，然后合并三角形倍增。

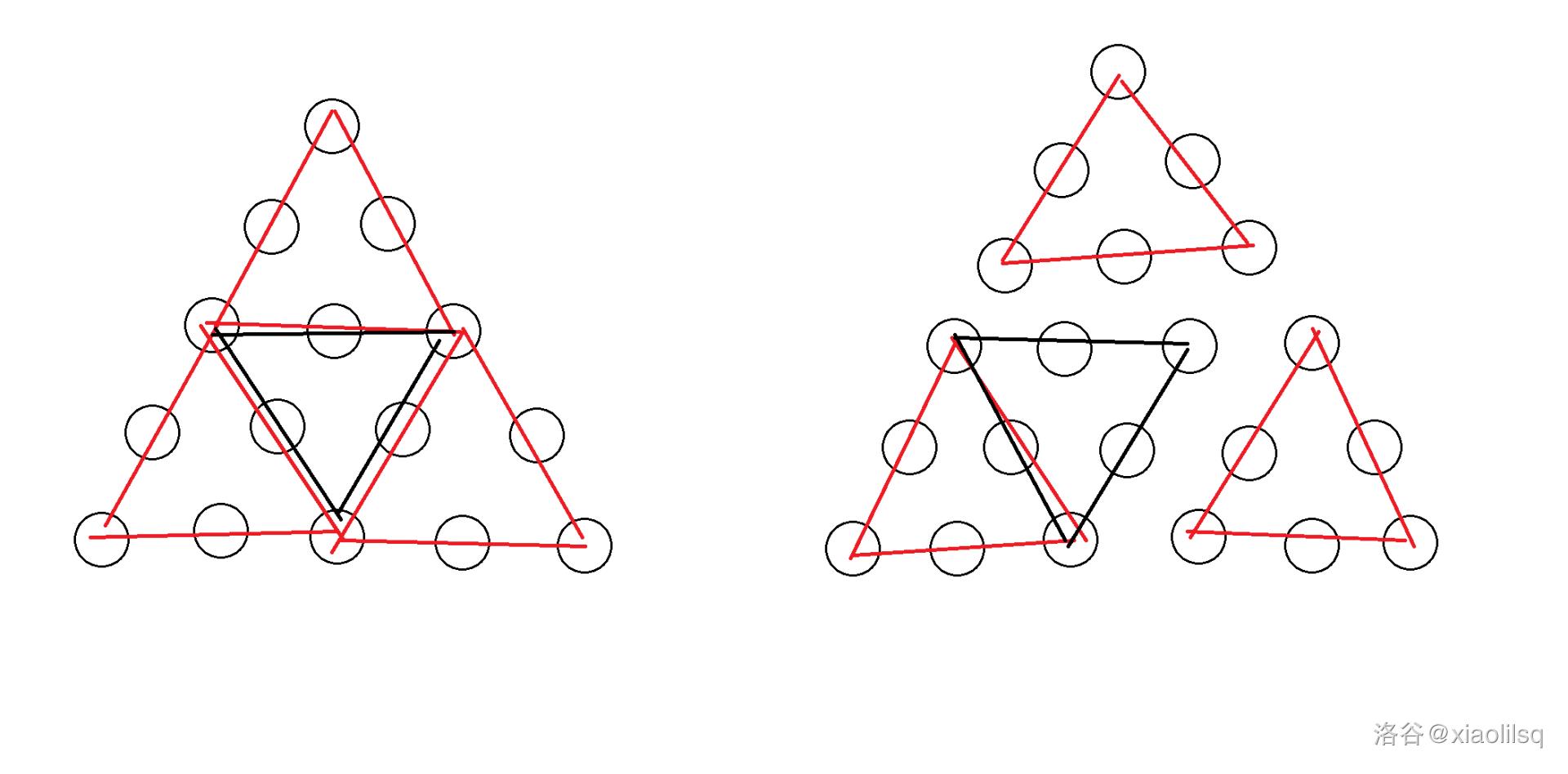
需要考虑优化空间，倍增这一维可省去，因为$k$​​给定了，滚动数组即可。

再优化起点，因为是一个三角形，没必要开矩形数组，所以三角形的大小作为第二维，第三位表示是否为倒三角即可。

时间复杂度：$O(n^{2}logk)$

代码参考题解区

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
	int f;char c;
	for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
	static char q[64];int cnt=0;
	if(!x)pc('0');if(x<0)pc('-'),x=-x;
	while(x)q[cnt++]=x%10+'0',x/=10;
	while(cnt--)pc(q[cnt]);
}
void ckmax(int &x,int y){
	if(x<y) x=y;
}
const int maxn=3005;
int cnt,s[15],dp[2][maxn*maxn/2][2],sm[maxn];
int main(){
	int n,k;
	read(n),read(k);
	int ck=k;
	while(ck>1){
		s[cnt++]=ck;
		ck=(ck+(ck&1))>>1;
	}
	for(int i=2;i<=n;++i)sm[i]=sm[i-1]+i-1;
	for(int i=1,a;i<=n;++i)
		for(int j=1;j<=i;++j)
			read(a),dp[cnt&1][sm[i]+j][0]=dp[cnt&1][sm[i]+j][1]=a;
	for(int c=cnt-1;~c;--c){
		int o=c&1,_o=!o,sk=s[c],nt=(s[c]+(s[c]&1))>>1;
		for(int i=1;i<=n;++i){
			for(int j=1;j<=i;++j){
				for(int rv=0;rv<2;++rv){
					int re=0;
					if(!rv&&i+sk-1>n)continue;
					if(rv&&i-sk+1<1)continue;
					if(!rv){
						ckmax(re,dp[_o][sm[i]+j][false]);
						ckmax(re,dp[_o][sm[i+sk-nt]+j][false]);
						ckmax(re,dp[_o][sm[i+sk-nt]+j+sk-nt][false]);
						ckmax(re,dp[_o][sm[i+sk-1]+j+nt-1][true]);
					}
					else{
						ckmax(re,dp[_o][sm[i]+j][true]);
						ckmax(re,dp[_o][sm[i-sk+nt]+j][true]);
						ckmax(re,dp[_o][sm[i-sk+nt]+j-sk+nt][true]);
						ckmax(re,dp[_o][sm[i-sk+1]+j-nt+1][false]);
					}
					dp[o][sm[i]+j][rv]=re;
				}
			}
		}
	}
	long long ans=0;
	for(int i=1;i<=n-k+1;++i){
		for(int j=1;j<=i;++j){
			ans+=dp[0][sm[i]+j][false];
		}
	}
	write(ans),pc('\\n');
	return 0;
}

P4403 [BJWC2008]秦腾与教学评估

转了弯的二分。考虑到奇数只有一个，所以可以用前缀和来二分，如果当前二分的区间$[l,m]$ 为奇数，显然答案在左区间，否则在右区间。

至于个数的话 就$O(n)$扫一遍特判$d_i|(x-s_i)$ 即可。

时间复杂度：$O(nlo201621123062《java程序设计》第九周作业总结$

20165201 课下作业第十周（选做）

20175325 实现mypwd(选做，加分)

第九次作业

数据结构-排序（选做） 20175204

20175314薛勐 数据结构-排序（选做）