2021牛客暑期多校训练营7，签到题FHI

Posted 2021-09-04 小哈里

题号 标题 已通过代码 通过率 团队的状态
A xay loves connected graphs 点击查看 7/117 未通过
B xay loves monotonicity 点击查看 39/349 未通过
C xay loves jumping 点击查看 1/85 未通过
D xay loves matrices 点击查看 12/114 未通过
E xay loves nim 点击查看 6/106 未通过
F xay loves trees 点击查看 374/2802 通过(dfs序，维护链)
G xay loves KDT 点击查看 1/125 未通过
H xay loves count 点击查看 1578/4193 通过（暴力枚举）
I xay loves or 点击查看 1733/7404 通过（贪心）
J xay loves Floyd 点击查看 59/357 未通过
K xay loves sequence 点击查看 35/375 未通过

F xay loves trees

题意：

• 给出两棵树，由这两棵树根据规则可以生成一个图，规则如下：如果u , v在第一棵树中满足其中一个点是另一个点祖先且最终所有所选的点都互相联通，在第二棵树中满足两个点都不是另外一个点的祖先，则u, v之间连一条边。
• 求最后生成的图中最大的团。(团为子图中的完全图)

思路：

• 原题来源，Codeforces Round #722 (Div. 1) C. Trees of Tranquillity，在树1加了一个联通的条件，改了好久都没改出来。
• 首先观察到一个比较重要的性质：选出来的点在第一棵树上构成一条链（且不能中断），所以我们在第一颗树上需要dfs。
• 再考虑到再第二棵树中 u,v 不存在祖先−子代关系。判断祖先和子代有无被选点可以用 dfs 序完成，我们先在第二棵树上求出每个点的dfs序，那么每个点的dfs序可以用一个区间表示[ in[u], out[u] ]表示， 一个点如果不在另一个点的子树内，那么他们的dfs序一定不相交，反之则一定包含。
• 对于第一棵树，我们可以遍历第一棵树的每条链，用链表last和nxt[]维护当前链条，每次将链中每个点的dfs序放入set中按照区间左端点从小到大排序，当访问到新的节点的时候，如果当前节点与之前的链中的节点有冲突，那么就不断去掉链条顶部的点直到不冲突为止，然后加入当前节点继续遍历。去掉节点的时候开临时数组记录，回溯的时候加回去即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 3e5+1010;
vector<int>G1[maxn], G2[maxn];

int tim, in[maxn], out[maxn], rev[maxn];
void pre(int x, int fa){   //跑dfs序
	in[x] = ++tim;  rev[tim]=x;
	for(int to: G2[x]){
		if(to!=fa)pre(to,x);
	}
	out[x] = tim;
}

int ans, last, nxt[maxn];//开链表维护当前链
set<int>se;
void dfs(int x, int fa){
	int tmplast = last;  vector<int>tmp;
	while(se.size()){//如果u和链里有节点冲突，那就不断去掉链顶节点
		int ok =1;
		auto it=se.lower_bound(in[x]);
		if(it!=se.end() && *it<=out[x])ok=0; //相交
		else if(it!=se.begin()){
			it--;
			if(*it<=in[x]&&in[x]<=out[rev[*it]])ok=0;//x在it子树内
		}
		if(ok)break;
		se.erase(in[last]);
		tmp.push_back(in[last]);//回溯的时候需要加回去
		last = nxt[last];  //不断去掉链顶节点
	}
	se.insert(in[x]);//加入当前节点
	ans = max(ans, (int)se.size());
	for(int to : G1[x]){
		if(to!=fa){
			nxt[x] = to;
			dfs(to, x);
		}
	}
	se.erase(in[x]);  //回溯删除并复原
	for(int y : tmp)se.insert(y);
	last = tmplast;
}

int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int T;  cin>>T;
	while(T--){
		int n;  cin>>n;
		for(int i=1; i<=n; i++)G1[i].clear(),G2[i].clear();
		for(int i = 1; i < n; i++){
			int x, y;  cin>>x>>y;
			G1[x].push_back(y);
			G1[y].push_back(x);
		}
		for(int i = 1; i < n; i++){
			int x, y;  cin>>x>>y;
			G2[x].push_back(y);
			G2[y].push_back(x);
		}
		tim = 0;  pre(1,0);
		ans = 0;  last = 1;  se.clear();  dfs(1,0);
		cout<<ans<<"\\n";
	}
	return 0;
}

H xay loves count

题意：

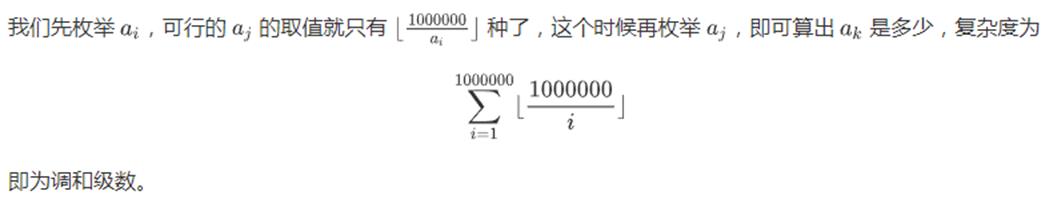
• 给出一个长为n的数组，求有多少对（i,j,k）满足ai*aj==ak，n<1e6

思路：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6+10;
int a[N];
int main(){
	int n;  cin>>n;
	for(int i=1; i <= n; i++){
		int x; cin>>x; a[x]++;
	}
	LL ans = 0;
	for(int i = 1; i < N; i++)
		for(int j = 1; j*i < N; j++)
			ans += a[i]*a[j]*a[i*j];
	cout<<ans<<"\\n";
	return 0;
}

I xay loves or

题意：

• 给出x和s，求有多少个整数y满足x or y == s

思路：

• 首先容易想到, x|y以后一定大于等于x，原本的1位还是1, 0位则是有机会被置为1，因为要等于s，所以原本s的0位，x必须是0，不然不论y这一位是什么都不行，即s&x==x必须满足，s的0位x不能是1，否则答案就是0。
• 然后再取y的每一位考虑，x的1位y可以随便取，剩下的位s是什么x就必须是什么，y也必须与之对应，没有选择，所以答案是2^(x的1位个数)。
• 注意如果x == s，因为y是正整数，所以要去掉y == 0的情况。

#include<bits/stdc++.h>
using namespace std;
int main(){
    int x, s;  cin>>x>>s;
	if((s&x)!=x){ cout<<"0\\n"; return 0; }
	long long ans = 1;
	for(int t=x; t; t-=t&(-t))ans*=2;
	if(x==s)ans--;
	cout<<ans<<"\\n";
	return 0;
}

---

注意到一个bug，s的范围也就1e7左右，可以直接暴力枚举？

#include<bits/stdc++.h>
using namespace std;
int main(){
    int x, s, y=0;  cin>>x>>s;
    for(int i=1;i<=s;i++)
        if((x|i)==s)y++;
	cout<<y<<"\\n";
	return 0;
}