R语言主成分分析（Principle Component AnalysisPCA）

Posted 2021-09-04 Data+Science+Insight

R语言主成分分析（Principle Component Analysis、PCA）

利用正交变换把可能线性相关变量表示的观测数据，转换为由少数几个线性无关变量（主成分）表示的数据。（重构原始特征空间；线性降维）

要尽可能保留原始数据中的信息，两个思路：最大投影方差、最小投影距离。

完全的无监督，只需要通过方差来衡量信息量（但也是一种局限性）。各个主成分正交，降维后不同维度特征之间不再有相关性（但失去维度的具体含义）。

主成分是初始变量的线性组合，用于替代初始变量并尽可能保留初始信息。如第一主成分：

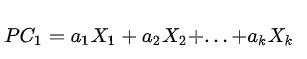
它是 k 个观测变量的加权组合，对初始变量集的方差解释性最大。

• 主成分分析 ( PCA ) 是指，用一组较少的不相关变量代替大量相关变量，同时尽可能保留初始变量的信息。值得注意的是，主成分是初始变量的线性组合。
• 因子分析 ( EFA ) 是指， 通过发掘隐藏在数据下的一组较少的、更为基本的无法观测的变量，来解释一组可观测变量的相关性。
• 区别：从定义上其实就很好理解，但是更简单的理解方式：把「因子分析」看作是求得「元素」，这些元素是组成初始变量的因子；而把「主成分分析」看作是求得一种「组合」，这些组合是初始变量配给不同系数组成的「组合」，且每个组合之间不相关。