机器学习建模中的Bagging思想！

Posted 2021-09-04 Wang_AI

 Datawhale干货 

作者：小偶，来源：偶数科技

我们在生活中做出的许多决定都是基于其他人的意见，而通常情况下由一群人做出的决策比由该群体中的任何一个成员做出的决策会产生更好的结果，这被称为群体的智慧。集成学习（Ensemble Learning）类似于这种思想，集成学习结合了来自多个模型的预测，旨在比集成该学习器的任何成员表现得更好，从而提升预测性能（模型的准确率），预测性能也是许多分类和回归问题的最重要的关注点。

集成学习（Ensemble Learning）是将若干个弱分类器（也可以是回归器）组合从而产生一个新的分类器。（弱分类器是指分类准确率略好于随机猜想的分类器，即error rate < 0.5)。

集成机器学习涉及结合来自多个熟练模型的预测，该算法的成功在于保证弱分类器的多样性。而且集成不稳定的算法也能够得到一个比较明显的性能提升。集成学习是一种思想。当预测建模项目的最佳性能是最重要的结果时，集成学习方法很受欢迎，通常是首选技术。

 

 

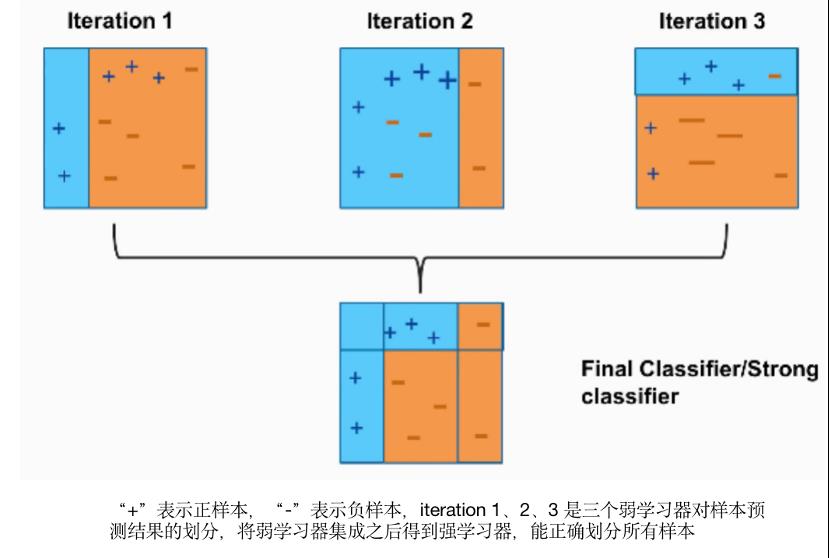
· 为什么要使用集成学习 ·

(1) 性能更好：与任何单个模型的贡献相比，集成可以做出更好的预测并获得更好的性能；

(2) 鲁棒性更强：集成减少了预测和模型性能的传播或分散，平滑了模型的预期性能。

(3) 更加合理的边界：弱分类器间存在一定差异性，导致分类的边界不同。多个弱分类器合并后，就可以得到更加合理的边界，减少整体的错误率，实现更好的效果；

(4) 适应不同样本体量：对于样本的过大或者过小，可分别进行划分和有放回的操作产生不同的样本子集，再使用样本子集训练不同的分类器，最后进行合并；

(5) 易于融合：对于多个异构特征数据集，很难进行融合，可以对每个数据集进行建模，再进行模型融合。

 

· 机器学习建模的偏差和方差 ·

机器学习模型产生的错误通常用两个属性来描述：偏差和方差。

偏差是衡量模型可以捕获输入和输出之间的映射函数的接近程度。它捕获了模型的刚性：模型对输入和输出之间映射的函数形式的假设强度。

模型的方差是模型在拟合不同训练数据时的性能变化量。它捕获数据的细节对模型的影响。

理想情况下，我们更喜欢低偏差和低方差的模型，事实上，这也是针对给定的预测建模问题应用机器学习的目标。模型性能的偏差和方差是相关的，减少偏差通常可以通过增加方差来轻松实现。相反，通过增加偏差可以很容易地减少方差。

与单个预测模型相比，集成用在预测建模问题上实现更好的预测性能。实现这一点的方式可以理解为模型通过添加偏差来减少预测误差的方差分量（即权衡偏差-方差的情况下）。

· 集成学习之Bagging思想 ·

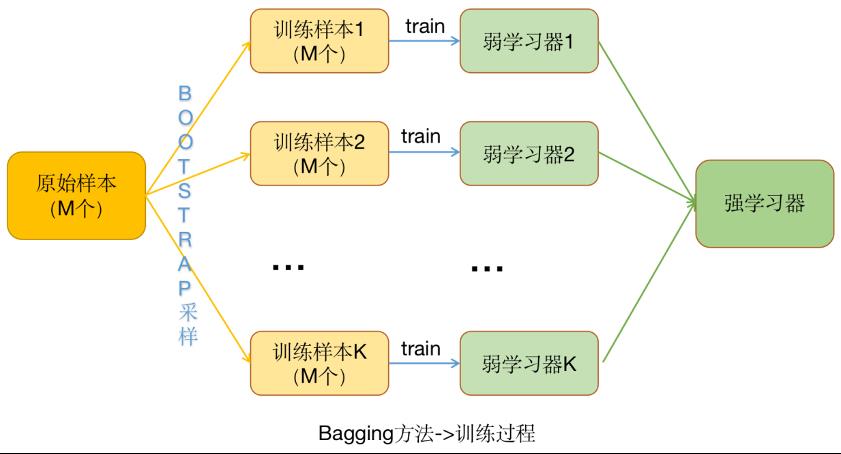
Bagging又称自举汇聚法（Bootstrap Aggregating），涉及在同一数据集的不同样本上拟合许多学习器并对预测进行平均，通过改变训练数据来寻找多样化的集成成员。

Bagging思想就是在原始数据集上通过有放回的抽样，重新选择出N个新数据集来分别训练N个分类器的集成技术。模型训练数据中允许存在重复数据。

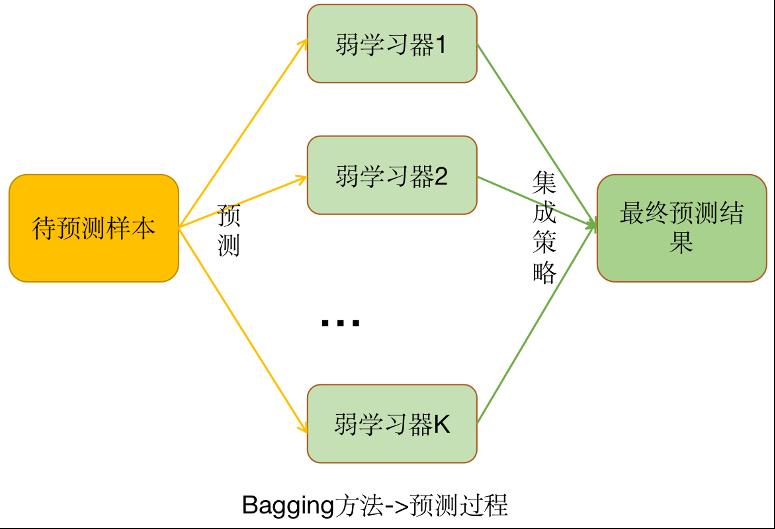
使用Bagging方法训练出来的模型在预测新样本分类的时候，会使用多数投票或者取平均值的策略来统计最终的分类结果。

基于Bagging的弱学习器（分类器/回归器）可以是基本的算法模型，如Linear、Ridge、Lasso、Logistic、Softmax、ID3、C4.5、CART、SVM、KNN、Naive Bayes等。

· 随机森林 (Random Forest) ·

随机森林算法原理

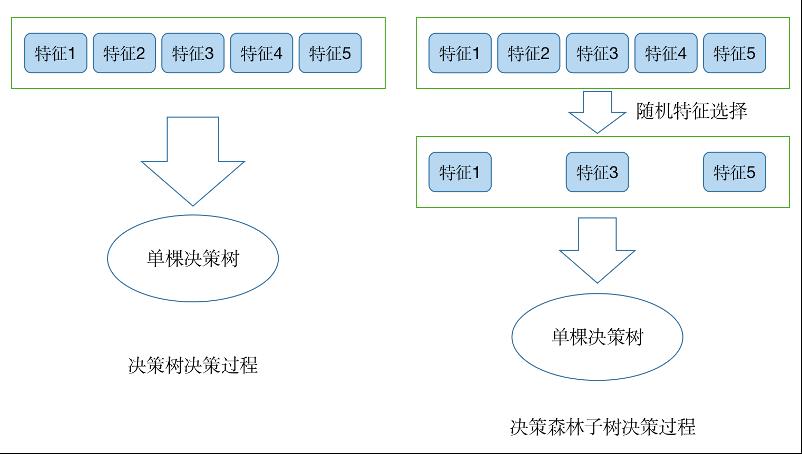
随机森林是在Bagging策略的基础上进行修改后的一种算法，方法如下：

(1) 使用Bootstrap策略从样本集中进行数据采样；

(2) 从所有特征中随机选择K个特征，构建正常决策树；

(3) 重复1，2多次，构建多棵决策树；

(4) 集成多棵决策树，形成随机森林，通过投票表决或取平均值对数据进行决策。

 

随机森林OOB Error

在随机森林中可以发现Bootstrap采样每次约有1/3的样本不会出现在Bootstrap所采样的样本集合中，当然也没有参加决策树的建立，而这部分数据称之为袋外数据OOB（out of bag),它可以用于取代测试集误差估计方法。

对于已经生成的随机森林，用袋外数据测试其性能，假设袋外数据总数为O，用这O个袋外数据作为输入，带进之前已经生成的随机森林分类器，分类器会给出O个数据相应的分类，因为这O条数据的类型是已知的，则用正确的分类与随机森林分类器的结果进行比较，统计随机森林分类器分类错误的数目，设为X，则袋外数据误差大小为X/O。

优点：这已经经过证明是无偏估计的，所以在随机森林算法中不需要再进行交叉验证或者单独的测试集来获取测试集误差的无偏估计。

缺点：当数据量较小时，Bootstrap采样产生的数据集改变了初始数据集的分布，这会引入估计偏差。

 

· 随机森林算法变种 ·

RF算法在实际应用中具有比较好的特性，应用也比较广泛，主要应用在：分类、归回、特征转换、异常点检测等。以下为常见的RF变种算法：

·Extra Trees (ET)

·Totally Random Trees Embedding (TRTE)

·Isolation Forest (IForest)

Extra Trees (ET)

Extra-Trees（Extremely randomized trees，极端随机树）是由Pierre Geurts等人于2006年提出。是RF的一个变种，原理基本和RF一样。但该算法与随机森林有两点主要的区别：

(1) 随机森林会使用Bootstrap进行随机采样，作为子决策树的训练集，应用的是Bagging模型；而ET使用所有的训练样本对每棵子树进行训练，也就是ET的每个子决策树采用原始样本训练；

(2) 随机森林在选择划分特征点的时候会和传统决策树一样（基于信息增益、信息增益率、基尼系数、均方差等），而ET是完全随机的选择划分特征来划分决策树。

对于某棵决策树，由于它的最佳划分特征是随机选择的，因此它的预测结果往往是不准确的，但是多棵决策树组合在一起，就可以达到很好的预测效果。

当ET构建完成，我们也可以应用全部训练样本得到该ET的误差。因为尽管构建决策树和预测应用的都是同一个训练样本集，但由于最佳划分属性是随机选择的，所以我们仍然会得到完全不同的预测结果，用该预测结果就可以与样本的真实响应值比较，从而得到预测误差。如果与随机森林相类比的话，在ET中，全部训练样本都是OOB样本，所以计算ET的预测误差，也就是计算这个OOB误差。

由于Extra Trees是随机选择特征值的划分点，会导致决策树的规模一般大于RF所生成的决策树。也就是说Extra Trees模型的方差相对于RF进一步减少。在某些情况下，ET具有比随机森林更强的泛化能力。

Totally Random Trees Embedding (TRTE)

TRTE是一种非监督学习的数据转化方式。它将低维的数据映射到高维，从而让映射到高维的数据更好的应用于分类回归模型。

TRTE算法的转换过程类似RF算法的方法，建立T个决策树来拟合数据。当决策树构建完成后，数据集里的每个数据在T个决策子树中叶子节点的位置就定下来了，将位置信息转换为向量就完成了特征转换操作。

例如，有3棵决策树，每棵决策树有5个叶子节点，某个数据特征x划分到第一个决策树的第3个叶子节点，第二个决策树的第1个叶子节点，第三个决策树的第5个叶子节点。则x映射后的特征编码为（0,0,1,0,0  1,0,0,0,0 0,0,0,0,1),有15维的高维特征。特征映射到高维之后，就可以进一步进行监督学习。

Isolation Forest (IForest)

IForest是一种异常点检测算法，使用类似RF的方式来检测异常点；IForest算法和RF算法的区别在于：

(1) 在随机采样的过程中，一般只需要少量数据即可；

(2) 在进行决策树构建过程中，IForest算法会随机选择一个划分特征，并对划分特征随机选择一个划分阈值；

(3) IForest算法构建的决策树一般深度max_depth是比较小的。

IForest的目的是异常点检测，所以只要能够区分异常数据即可，不需要大量数据；另外在异常点检测的过程中，一般不需要太大规模的决策树。

对于异常点的判断，则是将测试样本x拟合到T棵决策树上。计算在每棵树上该样本的叶子结点的深度ht(x)。从而计算出平均深度h(x)；然后就可以使用下列公式计算样本点x的异常概率值，p(s,m)的取值范围为[0,1]，越接近于1，则是异常点的概率越大。

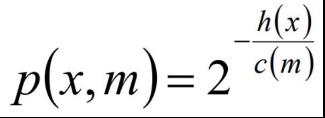
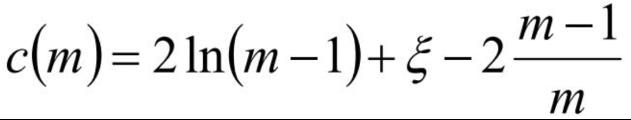
m为样本个数，ξ 为欧拉常数

 

· 随机森林优缺点总结 ·

 

本期AI小课堂我们一起了解了Bagging思想及其原理，以及基于Bagging的随机森林相关知识。最后，让我们一起总结下随机森林的优缺点：

 

优点

(1) 训练可以并行化，对于大规模样本的训练具有速度的优势；

(2) 由于进行随机选择决策树划分特征列表，这样在样本维度比较高的时候，仍然具有比较好的训练性能；

(3) 由于存在随机抽样，训练出来的模型方差小，泛化能力强；

(4) 实现简单；

(5) 对于部分特征缺失不敏感；

(6) 可以衡量特征的重要性。

缺点

(1) 在某些噪声比较大的特征上，易过拟合；

(2) 取值比较多的划分特征对RF的决策会产生更大的影响，从而有可能影响模型的效果。

觉得还不错就给我一个小小的鼓励吧！