卡尔曼滤波跟踪的相关概念与方程推导
Posted SoaringPigeon
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了卡尔曼滤波跟踪的相关概念与方程推导相关的知识，希望对你有一定的参考价值。
卡尔曼滤波跟踪的相关概念与方程推导
直接从数学公式和概念入手来考虑卡尔曼滤波无疑是一件非常枯燥的事情。为了便于理解，我们仍然从一个现实中的实例开始下面的介绍，这一过程中你所需的预备知识仅仅是高中程度的物理学内容。
假如现在有一辆在路上做直线运动的小车（如下所示），该小车在 t 时刻的状态可以用一个向量来表示，其中pt 表示他当前的位置，vt表示该车当前的速度。当然，司机还可以踩油门或者刹车来给车一个加速度ut，ut相当于是一个对车的控制量。显然，如果司机既没有踩油门也没有踩刹车，那么ut就等于0。此时车就会做匀速直线运动。
如果我们已知上一时刻 t-1时小车的状态，现在来考虑当前时刻t 小车的状态。显然有
p
t
=
p
t
−
1
+
v
t
−
1
∗
Δ
t
+
1
2
u
t
∗
Δ
t
2
v
t
=
v
t
−
1
+
u
t
∗
Δ
t
p_t = p_{t-1}+v_{t-1}*\\Delta t+\\frac{1}{2} u_t * \\Delta t^2\\\\ v_t = v_{t-1}+u_t * \\Delta t
pt=pt−1+vt−1∗Δt+21ut∗Δt2vt=vt−1+ut∗Δt
易知，上述两个公式中，输出变量都是输入变量的线性组合，这也就是称卡尔曼滤波器为线性滤波器的原因所在。既然上述公式表征了一种线性关系，那么我们就可以用一个矩阵来表示它，则有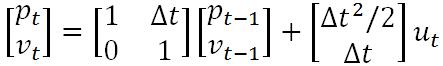
我们令其中，
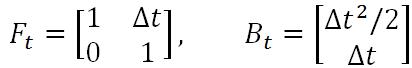
则得到卡尔曼滤波方程组中的第一条公式——状态预测公式，而
F
t
F_t
Ft 就是状态转移矩阵，它表示我们如何从上一状态来推测当前状态。而
B
t
B_t
Bt 则是控制矩阵，它表示控制量
u
t
u_t
ut 如何作用于当前状态。
x
^
t
−
=
F
t
x
^
t
−
1
+
B
t
u
t
(
1
)
\\hat{x}_t^- = F_t \\hat{x}_{t-1}+B_tu_t\\ \\ \\ \\ \\ (1)
x^t−=Ftx^t−1+Btut (1)
上式中
x
x
x 顶上的
^
\\hat{}
^ 表示为估计值（而非真实值）。等式左端部分的右上标
−
-
− 表示该状态是根据上一状态推测而来的，稍后我们还将对其进行修正以得到最优估计，修正之后才可以将
−
-
− 去掉。
既然我们是在对真实值进行估计，那么就理应考虑到噪声的影响。实践中，我们通常都是假设噪声服从一个0均值的高斯分布，即Noise~Guassian(0,σ)。例如对于一个一维的数据进行估计时，若要引入噪声的影响，其实只要考虑其中的方差 σ \\sigma σ即可。当我们将维度提高之后，为了综合考虑各个维度偏离其均值的程度，就需要引入协方差矩阵 Σ \\Sigma Σ。
回到我们的例子，系统中每一个时刻的不确定性都是通过协方差矩阵 Σ 来给出的。而且这种不确定性在每个时刻间还会进行传递。也就是说不仅当前物体的状态（例如位置或者速度）是会在每个时刻间进行传递的，而且物体状态的不确定性也是会在每个时刻间进行传递的。这种不确定性的传递就可以用状态转移矩阵来表示，即（注意，这里用到了前面给出的关于协方差矩阵的性质）
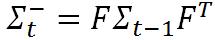
但是我们还应该考虑到，预测模型本身也并不绝对准确的，所以我们要引入一个协方差矩阵
Q
Q
Q 来表示预测模型本身的噪声（也即是噪声在传递过程中的不确定性），则有
Σ
t
−
=
F
Σ
t
−
1
F
T
+
Q
(
2
)
\\Sigma^-_t = F\\Sigma_{t-1}F^T+Q \\ \\ \\ \\ \\ (2)
Σt−=FΣt−1FT+Q (2)
这就是卡尔曼滤波方程组中的第二条公式，它表示不确定性在各个时刻间的传递关系。
继续我们的小汽车例子。你应该注意到，前面我们所讨论的内容都是围绕小汽车的真实状态展开的。而真实状态我们其实是无法得知的，我们只能通过观测值来对真实值进行估计。所以现在我们在路上布设了一个装置来测定小汽车的位置，观测到的值记为
X
(
t
)
X(t)
X(t) 。而且从小汽车的真实状态到其观测状态还有一个变换关系，这个变换关系我们记为
h
(
•
)
h(•)
h(•) ，而且这个
h
(
•
)
h(•)
h(•) 还是一个线性函数。此时便有
Y
(
t
)
=
h
[
X
(
t
)
]
+
V
(
t
)
Y(t) = h[X(t)]+V(t)
Y(t)=h[X(t)]+V(t)
其中
V
(
t
)
V(t)
V(t)表示观测的误差。既然
h
(
•
)
h(•)
h(•) 还是一个线性函数，所以我们同样可以把上式改写成矩阵的形式，则有
Y
t
=
H
x
t
+
v
Y_t = Hx_t +v
Yt=Hxt+v
由于
H
x
t
Hx_t
Hxt是一个一维的值，所以观测误差
v
v
v此时也是一个一维高斯分布参数
σ
\\sigma
σ的噪音
R
R
R。
接下来要做的事情就是对前面得出的状态估计进行修正，具体而言就是利用下面这个式子
x
^
t
=
x
^
t
−
+
K
t
(
y
t
−
H
x
^
t
−
)
(
4
)
\\hat{x}_t = \\hat{x}_t^-+K_t(y_t-H\\hat{x}_t^-)\\ \\ \\ \\ \\ (4)
x^t=x^t−+Kt(yt−Hx^t−) (4)
直观上来说，上式并不难理解。前面我们提到，
x
^
t
−
\\hat{x}_t^-
x^t− 是根据上一状态推测而来的，那么它与“最优”估计值之间的差距现在就是等式右端加号右侧的部分。
y
t
−
H
x
^
t
−
y_t-H\\hat{x}_t^-
yt−Hx^t−表示实际观察值与预估的观测值之间的残差。这个残差再乘以一个系数
K
t
K_t
Kt就可以用来对估计值进行修正。
K
t
K_t
Kt称为卡尔曼系数，它也是一个矩阵，它是对残差的加权矩阵，有的资料上称其为滤波增益阵
K
t
=
Σ
t
−
H
T
(
H
Σ
t
−
H
T
+
R
)
−
1
(
3
)
K_t = \\Sigma_t^-H^T(H\\Sigma_t^-H^T+R)^{-1} \\ \\ \\ \\ \\ (3)
Kt=Σt−HT(HΣt−HT+R)−1 (3)
我们可以定性地对这个系数进行解读：滤波增益阵首先权衡预测状态协方差矩阵
Σ
\\Sigma
Σ和观测值矩阵
R
R
R的大小，并以此来觉得我们是更倾向于相信预测模型还是详细观测模型。如果相信预测模型多一点，那么这个残差的权重就会小一点。反之亦然，如果相信观察模型多一点，这个残差的权重就会大一点。不仅如此，滤波增益阵还负责把残差的表现形式从观测域转换到了状态域。例如本题中观测值Z仅仅是一个一维的向量，状态 x 是一个二维的向量。所以在实际应用中，观测值与状态值所采用的描述特征或者单位都有可能不同，显然直接用观测值的残差去更新状态值是不合理的。而利用卡尔曼系数，我们就可以完成这种转换。例如，在小车运动这个例子中，我们只观察到了汽车的位置，但K里面已经包含了协方差矩阵P的信息（P里面就给出了速度和位置的相关性），所以它利用速度和位置这两个维度的相关性，从位置的残差中推算出了速度的残差。从而让我们可以对状态值 x 的两个维度同时进行修正。
最后，还需对最优估计值的噪音分布进行更新
Σ
t
=
(
I
−
K
t
H
)
Σ
t
−
(
5
)
\\Sigma_t = (I-K_tH)\\Sigma_t^- \\ \\ \\ \\ \\ (5)
Σt=(I−KtH)Σt卡尔曼滤波跟踪的相关概念与方程推导
滤波跟踪基于matlab扩展卡尔曼滤波器 (EKF) GPS 数据滤波跟踪含Matlab源码 2316期
滤波跟踪基于matlab扩展卡尔曼滤波器 (EKF) GPS 数据滤波跟踪含Matlab源码 2316期