[CF70D]Professor‘s task

Posted 2021-09-03 Tan_tan_tann

Professor’s task

题解

这道题很明显是让你动态维护凸包并判断点是否在凸包内。
这里给出一种很奇怪的动态维护凸包的方法，是笔者在上课时偶然想到的。
首先我们考虑凸包上的点具有什么特殊性质。

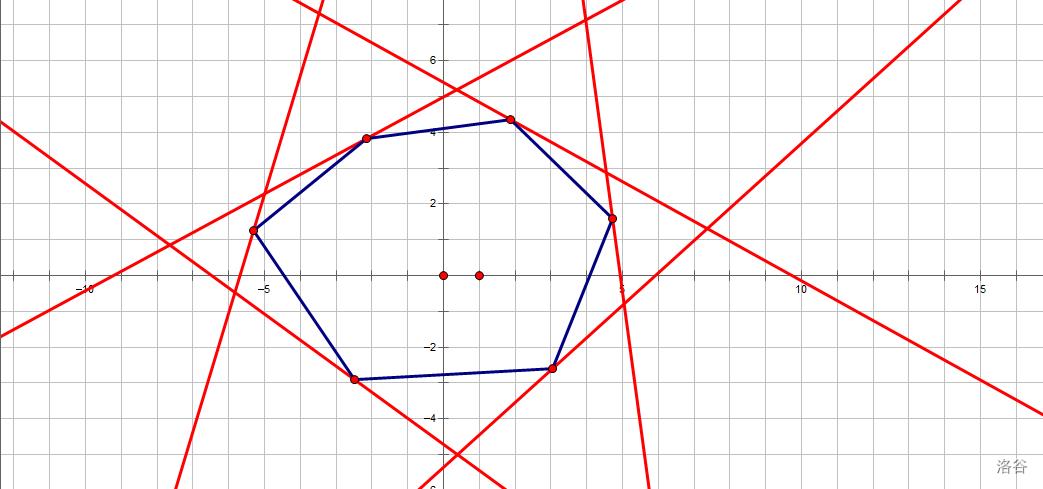
很明显，凸包上的点一定会存在一条为某个斜率的直线从无限远处向凸包平移时第一个碰到它，也就是这个点与这个凸包"相切"。
我们设对于凸包上的点 $(x,y)$，它的对应直线斜率为 $k$，明显有 $y=kx+b$。由于它是被第一个碰到的，所以 $b$ 要么是所有点中最大的，要么是所有点中最小的。
我们将直线的表达式改写成一般式 $ax+by=c$，我们的目的是让 $c$ 最小。
而当 $k$ 一定时 $a$ 与 $b$ 一定呈某种倍数关系，这个倍数是一定的，所以我们当 $a$ 一定时 $b$ 只与 $k$ 有关，我们不妨设 $a+b=1$，可得 $a{x}_0\pm (1-a)y_0=a(x_0\pm y_0)\mp y_0=c$。
同样在一般式中依旧有对于凸包上的点，存在某个斜率使得该点对应的 $c$ 是所有点中最大或者最小的，即 $\exists x,(x_0\pm y_0)x\mp y_0=\min ((x_i\pm y_i)x\mp y_i)$。
对于每个点，我们可以将 $c$ 的值与斜率的关系转化成一个一次函数：$f_i(x)=(x_i\pm y_i)x\mp y_i$。如果这个函数能在 $x\in [0,1]$ 中存在比其它的 $f$ 函数值都大/小的时候，那么它就一定是凸包上的点。

这明显可以用李超线段树来进行维护，$x$ 的取值区间为 $[0,1]$，在这个区间中用动态开点的方式维护所有点的函数，如果该函数在某个位置可以更新原线段树，那么它就可以成为凸包上的点。
插入一个点明显是 $\log n$ 的，直接像维护一次函数一样暴力插入即可。
而查询时可能出现它在这个位置上比当前节点的函数大，但却没有某个祖先的函数大的情况，所以我们需要在查询的过程中同时下传它比所有祖先的函数值都大的取值范围，这很明显可以直接解出来，在向子孙下传时需要更新，查询的时间复杂度仍然是 $\log n$。

总时间复杂度 $O\left(n\log n\right)$，但由于要维护四个函数，常数可能会有点大。

源码

#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 100005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
typedef long long LL;
typedef unsigned long long uLL;
const int mo=998244353;
const int jzm=2333;
const int lim=15;
const int orG=3,invG=332748118;
const double Pi=acos(-1.0);
const double eps=1e-7;
typedef pair<int,int> pii;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
	_T f=1;x=0;char s=getchar();
	while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
	while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
	x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
LL gcd(LL a,LL b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1LL)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1LL;}return t;}
int q,tot,root;
struct line{
	double k,b;line(){k=b=0;}
	line(double K,double B){k=K;b=B;}
	double ask(const double x){return k*x+b;}
};
struct ming{
	line mx,mn,nx,nn;int lson,rson;
	ming(){nx=mx=line(-1e9,-1e9);nn=mn=line(1e9,1e9);lson=rson=0;}
}tr[MAXN*10]; 
void insertMax(int &rt,double l,double r,line aw,int dep){
	if(l>r||!dep)return ;if(!rt)rt=++tot;const double mid=(l+r)/2.0;
	if(tr[rt].mx.ask(mid)<aw.ask(mid))swap(tr[rt].mx,aw);
	if(tr[rt].mx.ask(l)<aw.ask(l))insertMax(tr[rt].lson,l,mid,aw,dep-1);
	if(tr[rt].mx.ask(r)<aw.ask(r))insertMax(tr[rt].rson,mid,r,aw,dep-1);
}
void insertMin(int &rt,double l,double r,line aw,int dep){
	if(l>r||!dep)return ;if(!rt)rt=++tot;const double mid=(l+r)/2.0;
	if(tr[rt].mn.ask(mid)>aw.ask(mid))swap(tr[rt].mn,aw);
	if(tr[rt].mn.ask(l)>aw.ask(l))insertMin(tr[rt].lson,l,mid,aw,dep-1);
	if(tr[rt].mn.ask(r)>aw.ask(r))insertMin(tr[rt].rson,mid,r,aw,dep-1);
}
void insertNax(int &rt,double l,double r,line aw,int dep){
	if(l>r||!dep)return ;if(!rt)rt=++tot;const double mid=(l+r)/2.0;
	if(tr[rt].nx.ask(mid)<aw.ask(mid))swap(tr[rt].nx,aw);
	if(tr[rt].nx.ask(l)<aw.ask(l))insertNax(tr[rt].lson,l,mid,aw,dep-1);
	if(tr[rt].nx.ask(r)<aw.ask(r))insertNax(tr[rt].rson,mid,r,aw,dep-1);
}
void insertNin(int &rt,double l,double r,line aw,int dep){