吴恩达机器学习作业——异常检测和推荐系统

Posted 2021-09-03 挂科难

异常检测

参考资料：https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
先看数据：

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from scipy.io import loadmat
import math
data = loadmat('data/ex8data1.mat')  # Xval,yval,X
X = data['X']
Xval = data['Xval']
yval = data['yval']
plt.scatter(X[:,0], X[:,1])
plt.show()

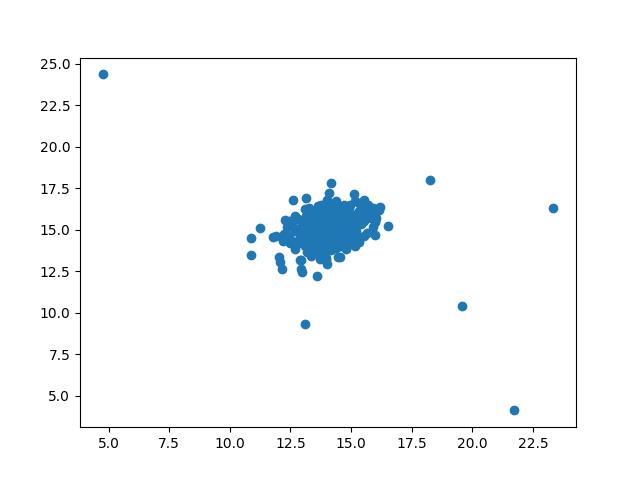
其中有几个点明显偏离中心，应该为异常数据点。下面我们让机器学会检测这些异常数据点：
首先根据两个特征建立两个高斯函数：

def estimate_gaussian(X):
    mu = X.mean(axis=0)  # X.mean()所有数取均值，X.mean(axis=0)取所有列的均值
    sigma = X.var(axis=0)  # 方差
    return mu, sigma


mu, sigma = estimate_gaussian(X)  # X每一个特征的均值（mu）和方差(sigma)


p = np.zeros((X.shape[0], X.shape[1]))  # X.shape = (307,2)
p0 = stats.norm(mu[0], sigma[0])
p1 = stats.norm(mu[1], sigma[1])
p[:,0] = p0.pdf(X[:,0])
p[:,1] = p1.pdf(X[:,1])

stats.norm根据传入的均值和方差自动创建高斯分布函数（正态分布），p0.pdf(x)将x带入建立好的高斯分布函数中得到输出。
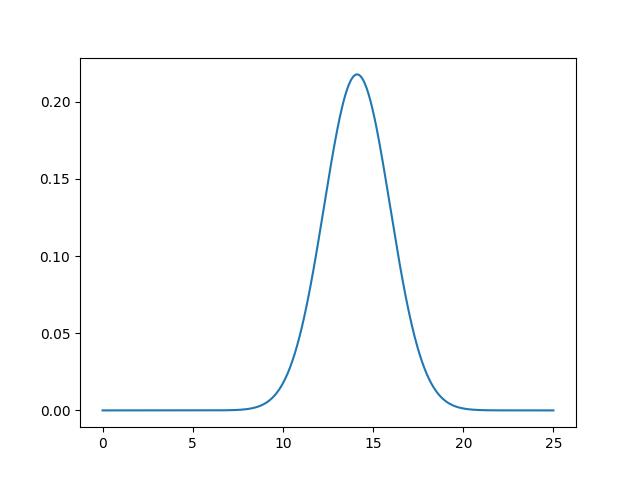
严谨起见笔者手动创建了一个高斯分布的函数：

def gussian(x,mu=mu[0], sigma=sigma[0]):
    s = 1/(math.sqrt(2*math.pi)*sigma)
    ss = np.exp(-1*(np.power((x-mu),2))/(2*np.power(sigma,2)))
    return s*ss

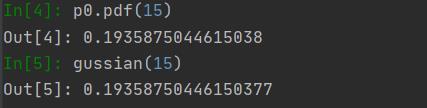
结果不能说一摸一样，也可以说是完全相同。（注：因为有两个特征。所以有两个高斯函数，这里只画出一个举例）

根据以下函数通过验证集与F1（查准率与查全率之间的权衡，可参考吴恩达学习笔记v5.51,166~168页）来寻找最佳阈值

def select_threshold(pval, yval):
    best_epsilon = 0
    best_f1 = 0

    step = (pval.max() - pval.min()) / 1000

    for epsilon in np.arange(pval.min(), pval.max(), step):
        preds = pval < epsilon
        #  np.logical_and逻辑与
        tp = np.sum(np.logical_and(preds == 1, yval == 1)).astype(float)
        fp = np.sum(np.logical_and(preds == 1, yval == 0)).astype(float)
        fn = np.sum(np.logical_and(preds == 0, yval == 1)).astype(float)

        precision = tp / (tp + fp)
        recall = tp / (tp + fn)
        f1 = (2 * precision * recall) / (precision + recall)

        if f1 > best_f1:
            best_f1 = f1
            best_epsilon = epsilon

    return best_epsilon, best_f1

然后再区分异常数据就很容易了，将X带入建立好的两个高斯函数得到异常概率，找到小于阈值的数据，标记，完成

p = np.zeros((X.shape[0], X.shape[1]))  # X.shape = (307,2)
p0 = stats.norm(mu[0], sigma[0])
p1 = stats.norm(mu[1], sigma[1])
p[:,0] = p0.pdf(X[:,0])
p[:,1] = p1.pdf(X[:,1])


pval = np.zeros((Xval.shape[0], Xval.shape[1]))  # Xval.shape = (307,2)
pval[:,0] = stats.norm(mu[0], sigma[0]).pdf(Xval[:,0])  # pval的第0列为验证集的第一个特征带入根据X第一个特征建立的高斯函数值
pval[:,1] = stats.norm(mu[1], sigma[1]).pdf(Xval[:,1])
epsilon, f1 = select_threshold(pval, yval)  # 用pval得到最佳阈值，再用阈值epsilon寻找p中的异常值
outliers = np.where(p < epsilon)
plt.scatter(X[:,0], X[:,1])
plt.scatter(X[outliers[0],0], X[outliers[0],1], s=50, color='r', marker='o')
plt.show()

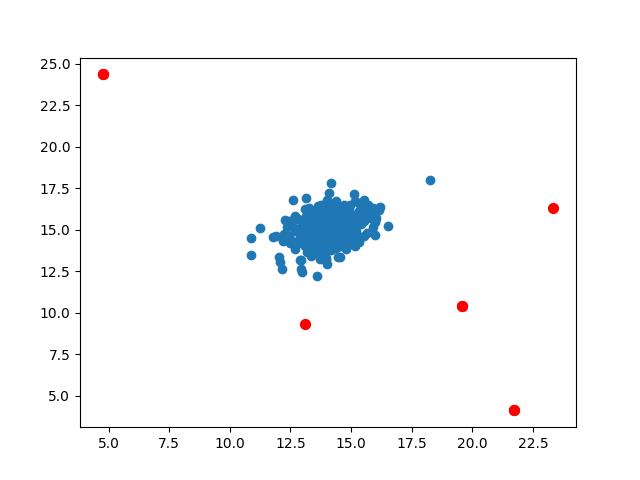
预测新数据时可以将两个特征的均值与方差及其阈值保存，在新代码中构建高斯分布函数，新特征带入小于阈值异常。

协同过滤

即推荐系统，太难了我giao。这一块弄了好久。能想出这个算法的人

代码如下：

import numpy as np
import scipy.optimize as opt
from scipy.io import loadmat


def serialize(X, theta):  # 展成一维再衔接
    return np.concatenate((X.ravel(), theta.ravel()))


def deserialize(param, n_movie, n_user, n_features):  # 再reshape成向量
    """into ndarray of X(1682, 10), theta(943, 10)"""
    return param[:n_movie * n_features].reshape(n_movie, n_features), \\
           param[n_movie * n_features:].reshape(n_user, n_features)


def cost(param, Y, R, n_features):
    """compute cost for every r(i, j)=1
    Args:
        param: serialized X, theta
        Y (movie, user), (1682, 943): (movie, user) rating
        R (movie, user), (1682, 943): (movie, user) has rating
    """
    # theta (user, feature), (943, 10): user preference
    # X (movie, feature), (1682, 10): movie features
    n_movie, n_user = Y.shape
    X, theta = deserialize(param, n_movie, n_user, n_features)

    inner = np.multiply(X @ theta.T - Y, R)

    return np.power(inner, 2).sum() / 2


def gradient(param, Y, R, n_features):
    # theta (user, feature), (943, 10): user preference
    # X (movie, feature), (1682, 10): movie features
    n_movies, n_user = Y.shape
    X, theta = deserialize(param, n_movies, n_user, n_features)

    inner = np.multiply(X @ theta.T - Y, R)  # (1682, 943)

    # X_grad (1682, 10)
    X_grad = inner @ theta

    # theta_grad (943, 10)
    theta_grad = inner.T @ X

    # roll them together and return
    return serialize(X_grad, theta_grad)


def regularized_cost(param, Y, R, n_features, l=1):
    reg_term = np.power(param, 2).sum() * (l / 2)

    return cost(param, Y, R, n_features) + reg_term


def regularized_gradient(param, Y, R, n_features, l=1):
    grad = gradient(param, Y, R, n_features)
    reg_term = l * param

    return grad + reg_term


data = loadmat('data/ex8_movies.mat')
# params_data = loadmat('data/ex8_movieParams.mat')
Y = data['Y']  # 评的几颗星，没评为0  1682款电影，943位用户
R = data['R']  # 评分为1，没评为0  shape=(1682,943)

# X = params_data['X'] # 电影参数.shape=(1682,10)
# theta = params_data['Theta']  # 用户参数.shape(943,10)
movie_list = []
with open('data/movie_ids.txt') as f:
    for line in f:
        tokens = line.strip().split(' ')  #去除两端空白再分
        movie_list.append(' '.join(tokens[1:])) # 去掉数字，仅将电影名称存入列表
movie_list = np.array(movie_list)


# 假设我给1682部电影中的某些评了分
ratings = np.zeros(1682)

ratings[0] = 4
ratings[6] = 3
ratings[11] = 5
ratings[53] = 4
ratings[63] = 5
ratings[65] = 3
ratings[68] = 5
ratings[97] = 2
ratings[182] = 4
ratings[225] = 5
ratings[354] = 5

#  插入后ratting将在0的位置（按列插入）Y(评的几颗星),R(评没评分)
# 自己为用户0
Y = np.insert(Y, 0, ratings, axis=1)  # now I become user 0
R = np.insert(R, 0, ratings != 0, axis=1)
movies, users = Y.shape  # (1682,944)
n_features = 10
X = np.random.random(size=(movies, n_features))
theta = np.random.random(size=(users, n_features))
lam = 1
Ymean = np.zeros((movies, 1))
Ynorm = np.zeros((movies, users))
param = serialize(X, theta)
# 均值归一化
for i in range(movies):  #R.shape = (1682,944),movies = 1682
    idx = np.where(R[i,:] == 1)[0]  # 第i部电影，用户0。找到用户0评过分的电影
    Ymean[i] = Y[i,idx].mean()  # 第i行,评过分的求平均
    Ynorm[i,idx] = Y[i,idx] - Ymean[i]  # 评过分的减去他们的均值

res = opt.minimize(fun=regularized_cost,
                   x0=param,
                   args=(Ynorm, R, n_features,lam),
                   method='TNC',
                   jac=regularized_gradient)
X = np.mat(np.reshape(res.x[:movies * n_features], (movies, n_features)))
theta = np.mat(np.reshape(res.x[movies * n_features:], (users, n_features)))
predictions = X * theta.T
my_preds = predictions[:, 0] + Ymean
sorted_preds = np.sort(my_preds, axis=0)[::-1]
idx = np.argsort(my_preds, axis=0)[::-1]

print("Top 10 movie predictions:")
for i in range(10):
    j = int(idx[i])
    print('Predicted rating of {} for movie {}.'.format(str(float(my_preds[j])), movie_list[j]))

每次运行结果不可能完全一致，我们的目的是是根据所拥有的评分建模，找到你可能喜欢的，再加上随机初始化的问题，结果不可能每次都一样。但总体来说是可行的，举个栗子，Return of the Jedi (1983)，Star Wars (1977)等电影经常排在前10，甚至前5.

当然也可以让特征值n_feature=50,可能会更准确一些，但运算量直接上升好几个数量级，粗略掐了下表，结果非常amazing啊，给pycharm 4G的运行内存算了13分钟多。