最短路径问题之Floyd算法（C语言）

Posted 2021-09-03 bfhonor

一、单源最短路径

（一）Floyd算法（带权图、无权图）

• Floyd算法：求出每⼀对顶点之间的最短路径
• 使⽤动态规划思想，将问题的求解分为多个阶段
• 对于n个顶点的图G，求任意⼀对顶点 Vi —> Vj 之间的最短路径可分为如下⼏个阶段：
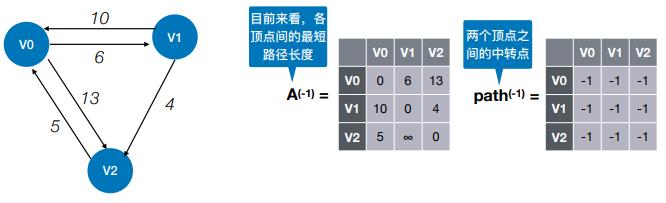
  #初始：不允许在其他顶点中转，最短路径是？
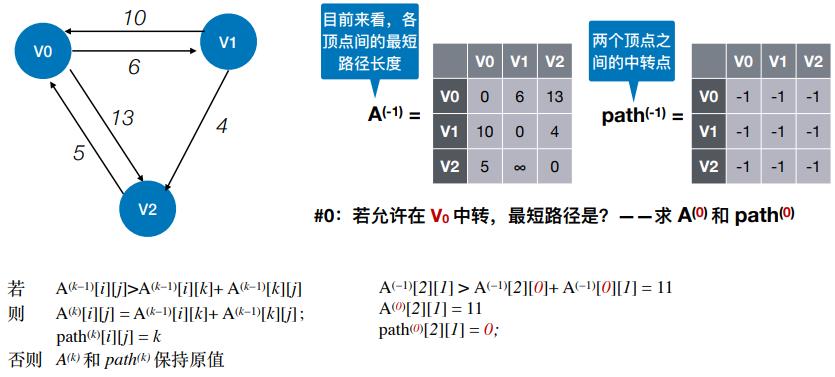
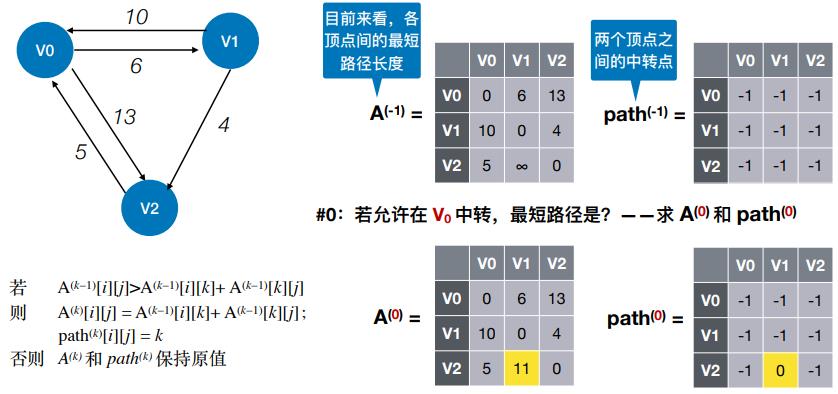
  #0：若允许在 V0 中转，最短路径是？
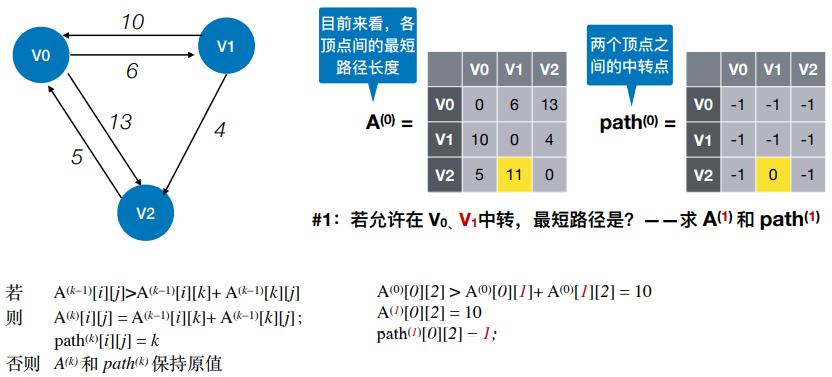
  #1：若允许在 V0、V1 中转，最短路径是？
  #2：若允许在 V0、V1、V2 中转，最短路径是？
  …
  #n-1：若允许在 V0、V1、V2 …… Vn-1 中转，最短路径是？

（二）算法思想

• #初始：不允许在其他顶点中转，最短路径是？
  
• #0：若允许在 V₀ 中转，最短路径是？——求 A⁽⁰⁾ 和 path⁽⁰⁾
  
  
• #1：若允许在 V₀、V₁ 中转，最短路径是？——求 A⁽¹⁾ 和 path⁽¹⁾
  
  
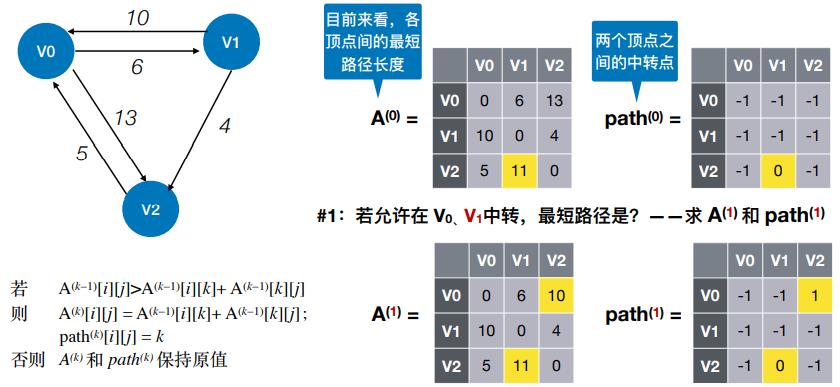
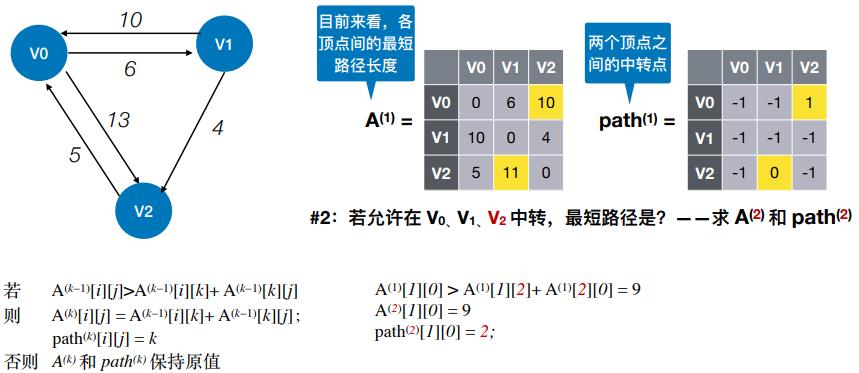
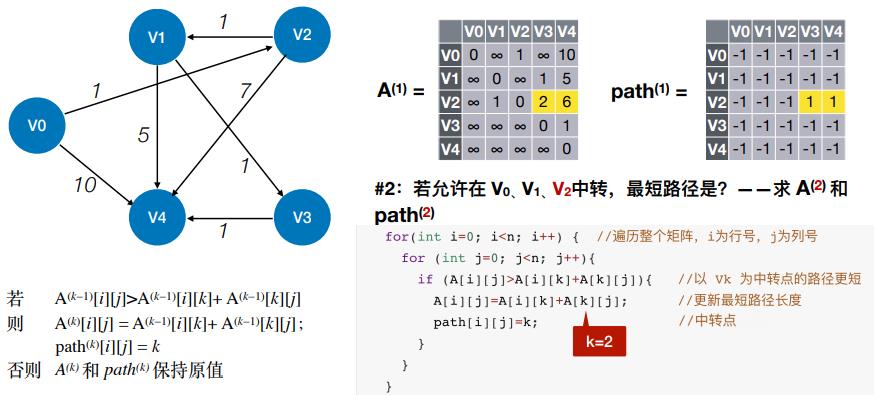
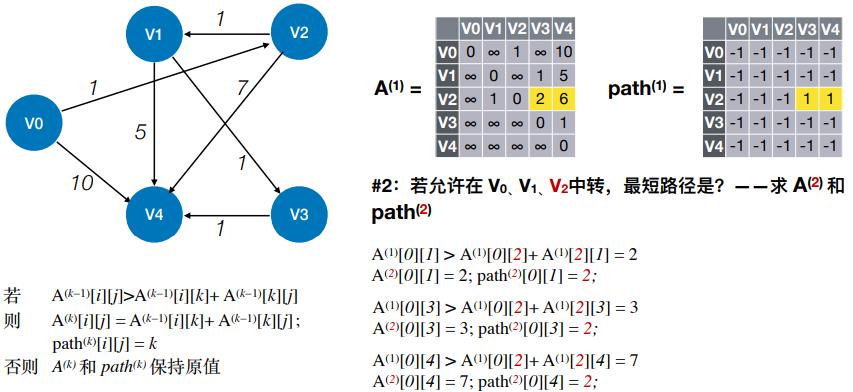
• #2：若允许在 V₀、V₁、V₂ 中转，最短路径是？——求 A⁽²⁾ 和 path⁽²⁾
  
  
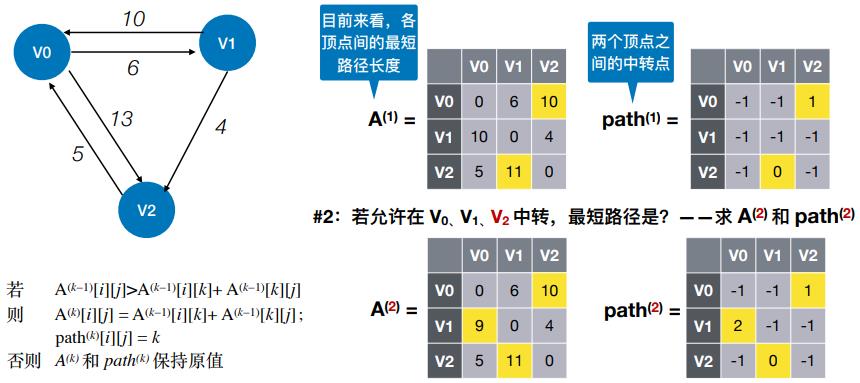
• 从A(-1) 和 path(-1) 开始，经过 n 轮递推，得到 A(n-1) 和 path(n-1)
  

（三）Floyd算法核心代码

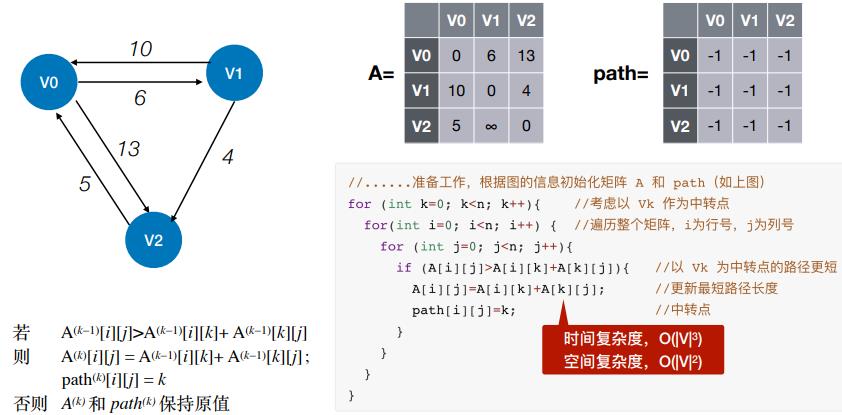
（四）Floyd算法实例

• #初始：不允许在其他顶点中转，最短路径是？
  
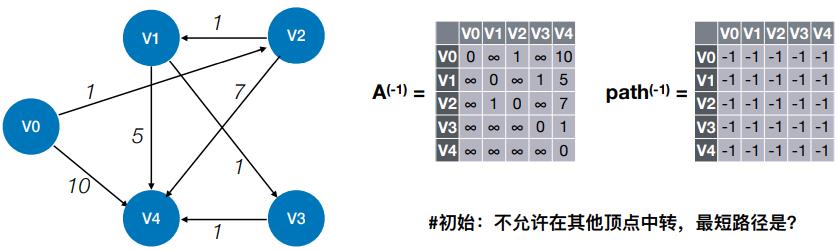
• #0：若允许在 V₀ 中转，最短路径是？——求 A⁽⁰⁾ 和 path⁽⁰⁾
  
  
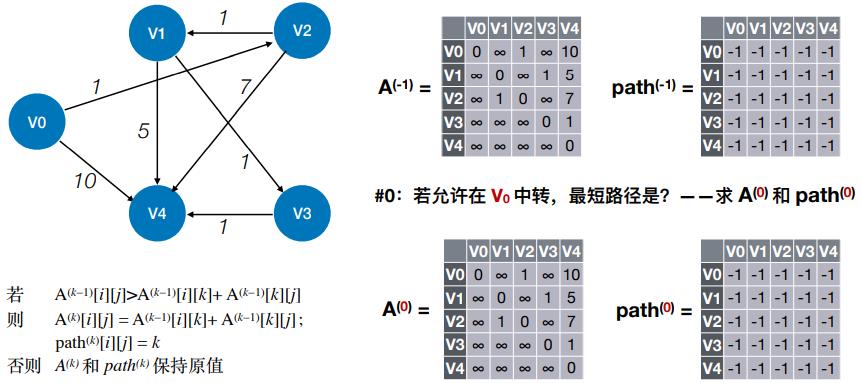
• #1：若允许在 V₀、V₁ 中转，最短路径是？——求 A⁽¹⁾ 和 path⁽¹⁾
  
  
  
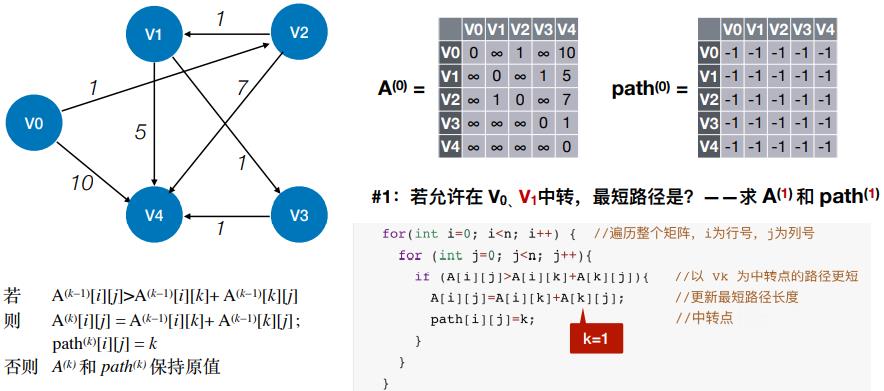
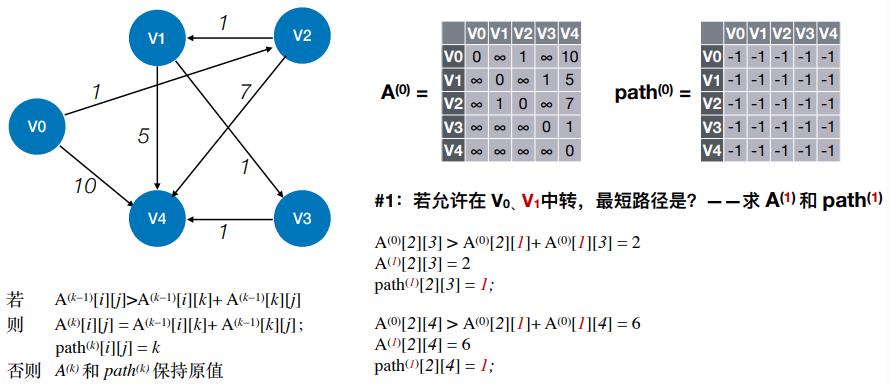
• #2：若允许在 V₀、V₁、V₂ 中转，最短路径是？——求 A⁽²⁾ 和 path⁽²⁾
  
  
  
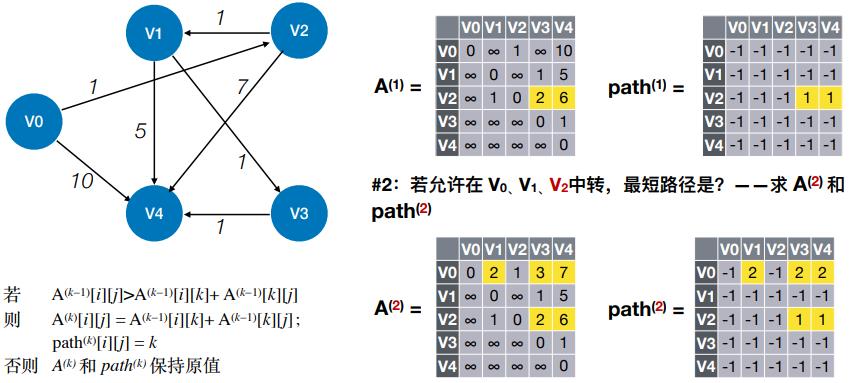
• #3：若允许在 V₀、V₁、V₂、V₃ 中转，最短路径是？——求 A⁽³⁾ 和 path⁽³⁾
  
  
  
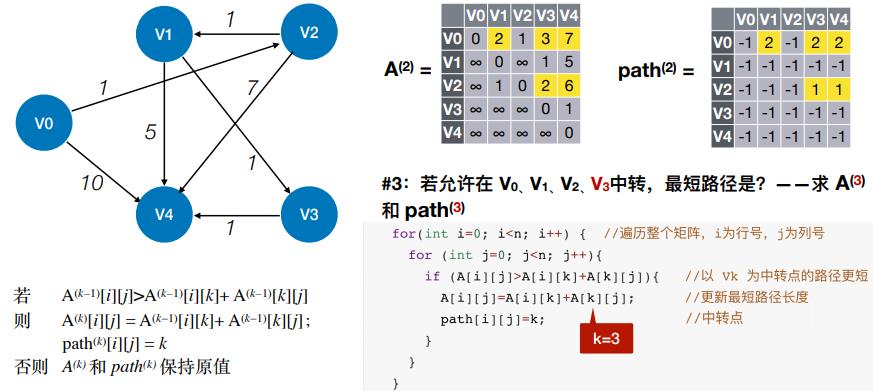
• #4：若允许在 V₀、V₁、V₂、V₃V₄ 中转，最短路径是？——求 A⁽⁴⁾ 和 path⁽⁴⁾
  
  
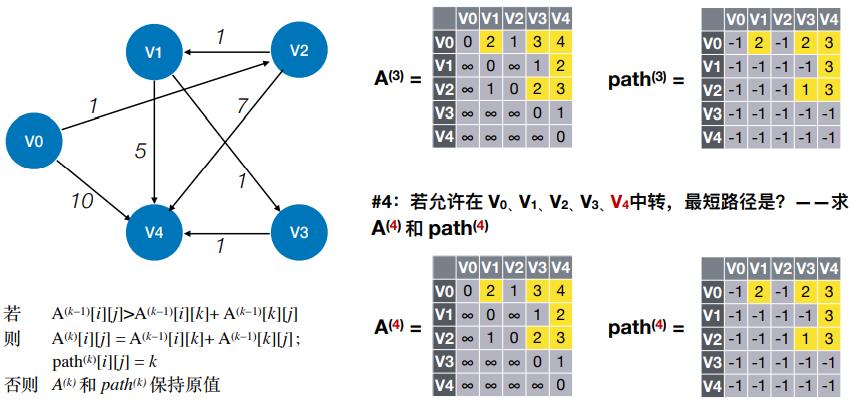
• V0到V4 最短路径长度为 A[0][4]=4
  

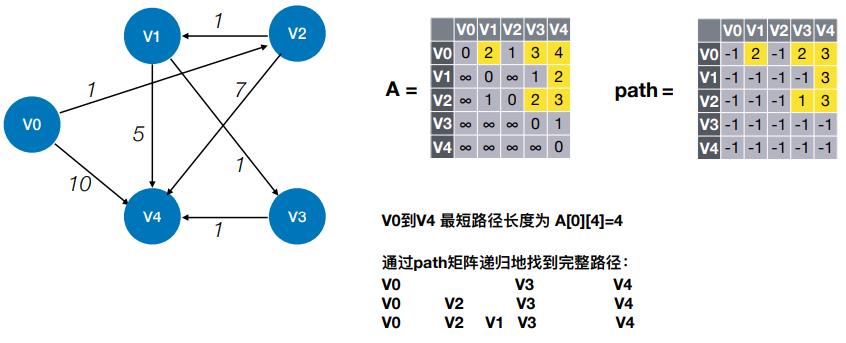
（五）Floyd算法用于负权图

（六）局限性——不能解决的问题

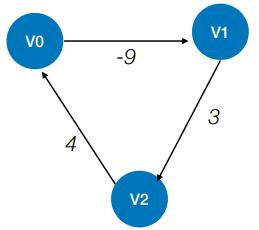
• Floyd 算法不能解决带有“负权回路”的图（有负权值的边组成回路），这种图有可能没有最短路径

（七）BFS算法 vs Dijkstra算法 vs Floyd算法

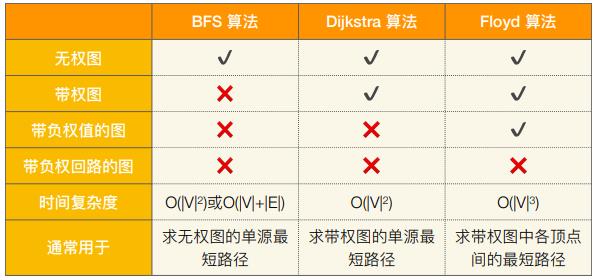
• 注：也可⽤ Dijkstra 算法求所有顶点间的最短路径，重复 |V| 次即可，总的时间复杂度也是O(|V|3)