最小生成树的Prim算法以及Kruskal算法（C语言）

Posted 2021-09-03 bfhonor

一、最小生成树

• 连通图的生成树是包含图中全部顶点的一个极小连通子图。
• 边尽可能的少，但要保持连通
• 若图中顶点数为n，则它的生成树含有 n-1 条边。对生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会形成一个回路。
  

（一）最小生成树（最小代价树）

• 对于⼀个带权连通⽆向图G = (V, E)，⽣成树不同，每棵树的权（即树中所有边上的权值之和）也可能不同。设R为G的所有⽣成树的集合，若T为R中边的权值之和最⼩的⽣成树，则T称为G的最⼩⽣成树（Minimum-Spanning-Tree，MST）
  
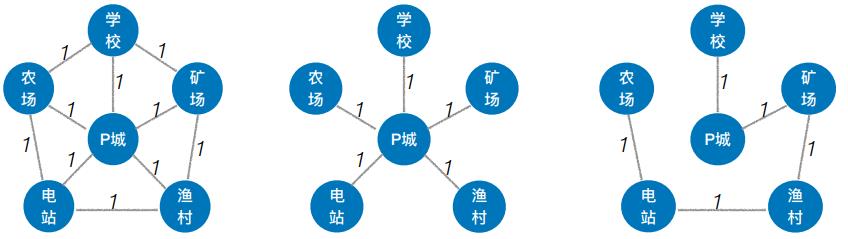
• 最小生成树可能有多个，但边的权值之和总是唯一且最小的
• 最小生成树的边数 = 顶点数 - 1。砍掉一条则不连通，增加一条边则会出现回路
  

（二）Prim 算法（普里姆）

• Prim 算法（普里姆）：从某一个顶点开始构建生成树；每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止。
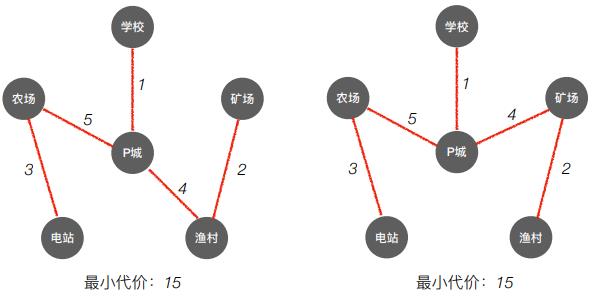
• 从P城开始进行建成生成树。
  
• 从农场开始进行建成生成树。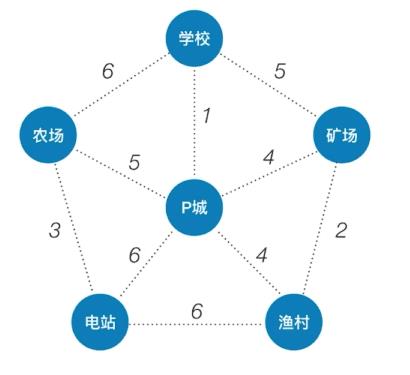
• 通过不同的结点开始，建成的最小生成树结构有可能不一样。
  

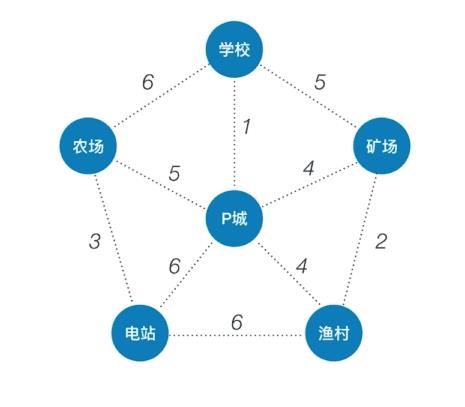
（三）Kruskal 算法（克鲁斯卡尔）

• Kruskal 算法（克鲁斯卡尔）：每次选择⼀条权值最⼩的边，使这条边的两头连通（原本已经连通的就不选）直到所有结点都连通。
  

（四）Prim 算法 v.s. Kruskal 算法

1. Prim 算法的实现思想

• 初始：从V0开始
  
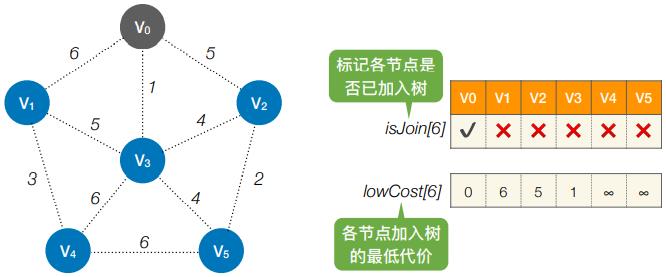
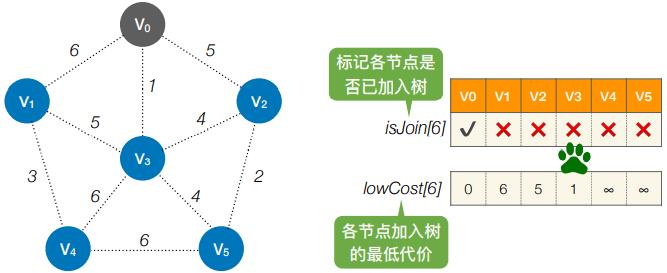
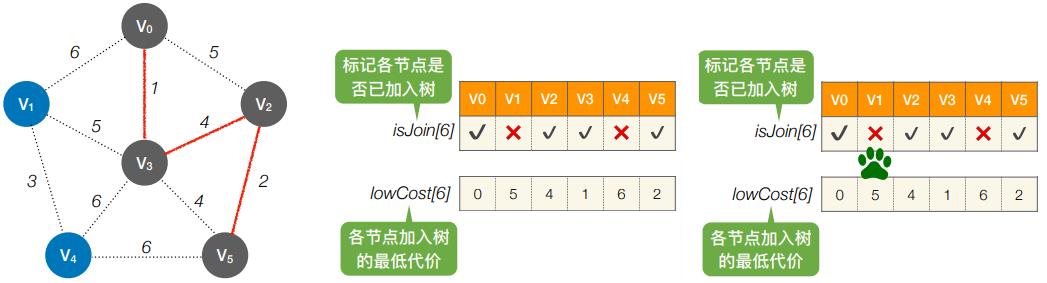
• 第1轮：循环遍历所有个结点，找到lowCost最低的，且还没加⼊树的顶点
  
  
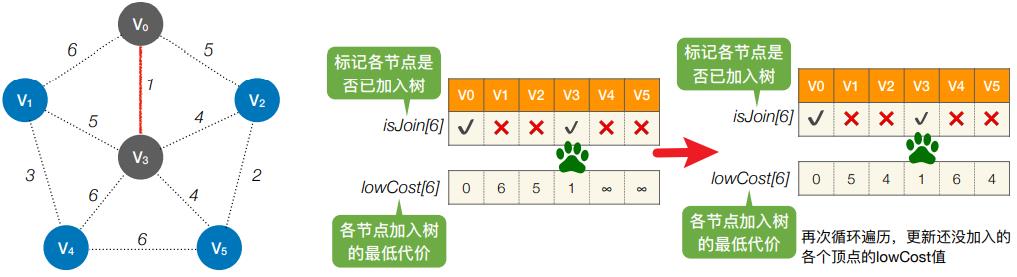
• 第2轮：循环遍历所有个结点，找到lowCost最低的，且还没加⼊树的顶点
  
  
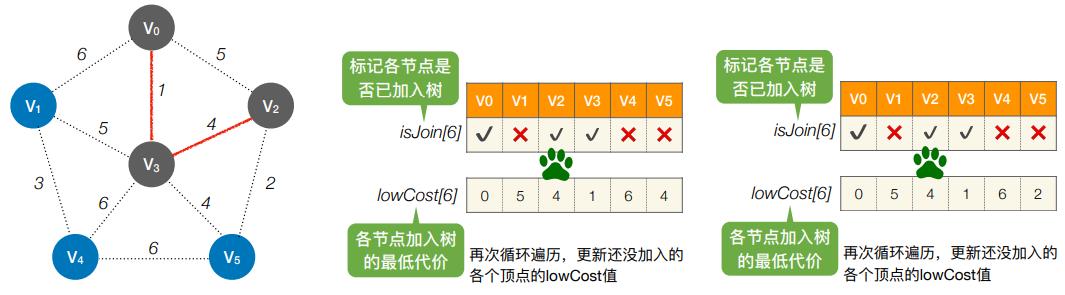
• 第3轮：循环遍历所有个结点，找到lowCost最低的，且还没加⼊树的顶点
  
  
• 第4轮：循环遍历所有个结点，找到lowCost最低的，且还没加⼊树的顶点
  
  
  
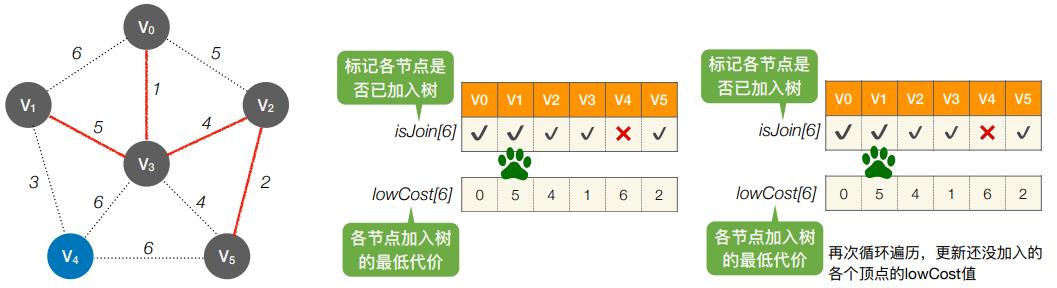
• 第5轮：循环遍历所有个结点，找到lowCost最低的，且还没加⼊树的顶点
  
  
  

2. Kruskal 算法的实现思想

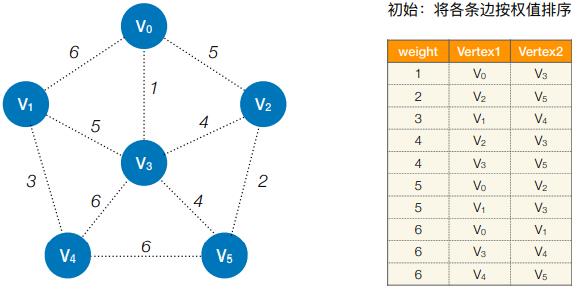
• 初始：将各条边按权值排序
  
• 第1轮：检查第1条边的两个顶点是否连通（是否属于同⼀个集合）
  
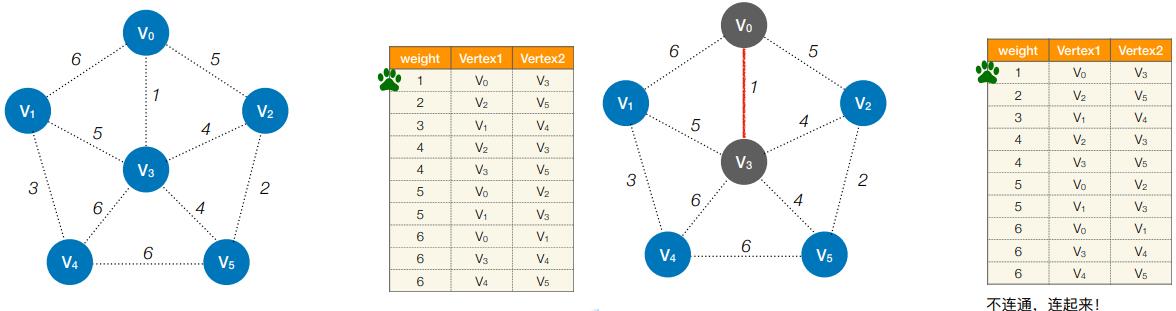
• 第2轮：检查第2条边的两个顶点是否连通（是否属于同⼀个集合）
  
• 第3轮：检查第3条边的两个顶点是否连通（是否属于同⼀个集合）
  
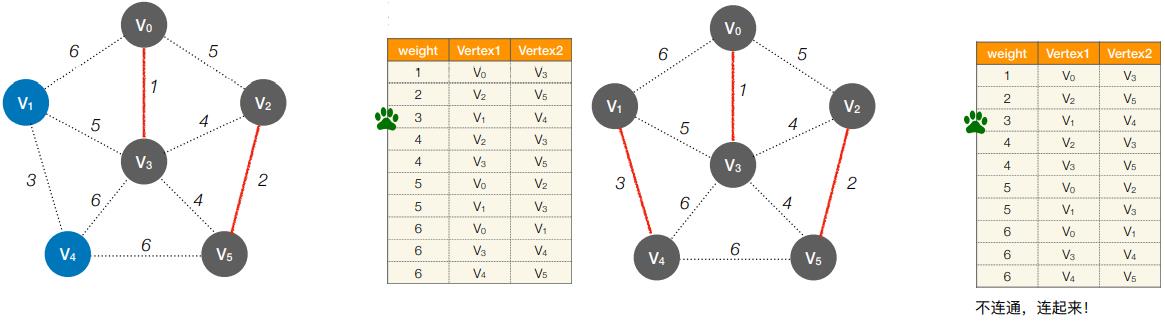
• 第4轮：检查第4条边的两个顶点是否连通（是否属于同⼀个集合）
  
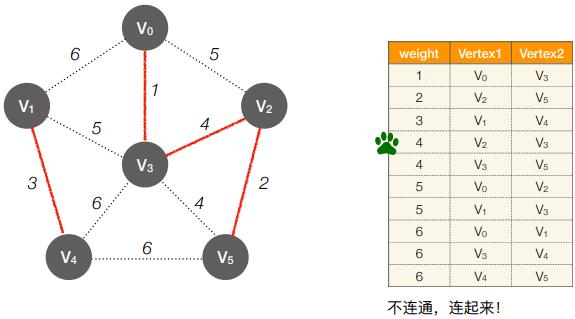
• 第5轮：检查第5条边的两个顶点是否连通（是否属于同⼀个集合）
  
• 第6轮：检查第6条边的两个顶点是否连通（是否属于同⼀个集合）
  
• 共执⾏ e 轮，每轮判断两个顶点是否属于同⼀集合，需要 O(log₂e)总时间复杂度 O(elog₂e)