(计算机组成原理)第二章数据的表示和运算-第三节2：IEEE754标准

Posted 2021-09-03 快乐江湖

文章目录

• 一：移码
• • （1）移码回顾
  • （2）偏置值
• 二：IEEE 754标准
• • （1）IEEE 754标准格式
  • （2）转换方法
  • （3）表示范围

一：移码

（1）移码回顾

本节内容涉及移码，有关移码的基础内容请移步

(计算机组成原理)第二章数据的表示和运算-第二节1：定点数的表示（原码、反码、补码和移码）

（2）偏置值

前面我们说过：移码是在补码的基础上将符号位取反得到的

其实移码的真正定义为：移码=真值+偏置值，只不过前面的讲述中我们的偏置值取定为了$2^7=128$，也即1000 0000。所以，假如真值为-127，也即-11111111，那么其所对应的移码就是-11111111+1000000000=0000 0001，其余数值也是这样。
所以表格中显示出的就好像是只是把符号位取反一样

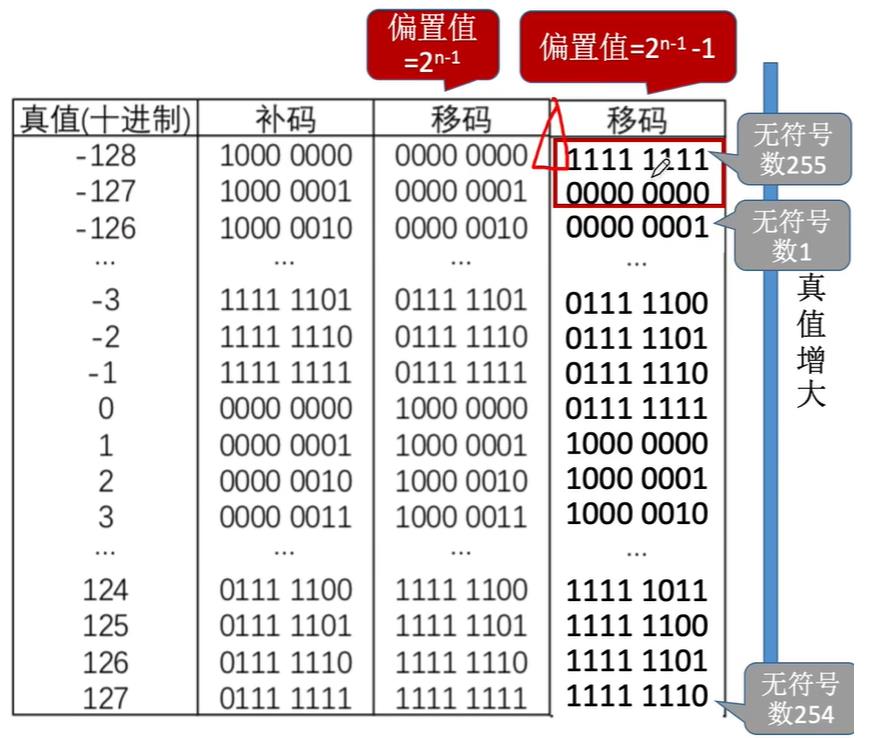
其实，偏置值也是可以设置为其他值的。比如今天我们学习的浮点数当中的IEEE754标准中，就用移码表示阶码，其偏置值取$2^{n-1}-1$，也即0111 1111（127）

这样的偏置值就导致移码会产生两个非常特殊的状态：1111 1111和0000 0000（真值-128和-127），它们都对应无符号数255；从真值-126开始，对应无符号数1，一直到无符号数254

二：IEEE 754标准

（1）IEEE 754标准格式

IEEE 754将浮点数分为短浮点数、长浮点数和临时浮点数三类，C语言遵循这个标准，因此它们分别对应float、double和long double

• 数符：表示了整个浮点数的正负性
• 阶码：采用移码表示，并且短浮点数的偏置值为127。所以原本8位的移码表示的真值范围为-128~127，但是127的偏置值会使真值-127和-128较为特殊，其移码是全0和全1，全0和全1在该标准具有特殊作用，所以实际上8位的阶码表示真值的范围应该是-126到127
• 尾数：注意采用原码表示。并且我们知道使用原码表示浮点需要进行规格化，也就是最高位格式应该是1.M，所以短浮点数这里尾数部分写的虽然是23位，但是实则是24位，一位暗含。

（2）转换方法

我们知道移码等于真值阶码+偏置值，那么自然而然阶码真值=移码-偏置值
因此IEEE 754标准中，规格化的短浮点数和长浮点数的真值分别为：
$$(-1{)}^s\times 1.M\times 2^{E-127}$$$$(-1{)}^s\times 1.M\times 2^{E-1023}$$

上式中，$s=0$表示正数，$s=1$表示负数

---

$case:$将十进制数-0.75转化为IEEE 754de1单精度浮点数格式表示（十进制转换为浮点数）
答：转换步骤如下

• 将十进制数转化为二进制数并规格化：$(-0.75{)}_{10}\stackrel{转换为二进制}{\to }(-0.11{)}_2\stackrel{浮点数规格化}{\to }(-1.1{)}_2\times 2^{-1}$
• 确定数符号：可以看出是负数，因此数符为1
• 确定尾数部分：前面说过暗含了高位为1，因此尾数部分是.100000...
• 确定阶码真值：基数指数部分是-1，因此阶码指针是-1
• 确定偏移值：127
• 确定移码：移码=-1+ 0111 1111=0111 1110（126，注意凑够8位）
• 最终形式（红色是数符，蓝色是阶码，绿色是尾数）：1 01111110 10000000000000000000000000000000

---

$case：$IEEE 754的单精度浮点数C0 A0 00 00的值为多少
答：转换步骤如下

• 将十六进制转化为二进制（红色是数符，蓝色是阶码，绿色是尾数）：1100 0000 1010 0000 0000 0000 0000 0000
• 数符为1：这是个负数
• 确定尾数部分：.01000，因此尾数真值为$1.01_2$
• 确定移码：是10000001，可看作无符号数129
• 确定偏移值：127
• 确定阶码真值：阶码真值=移码-偏移值=1000 0001-0111 1111=(0000 0010)${}_2$=$(2{)}_{10}$
• 确定浮点数真值：根据公式$(-1{)}^s\times 1.M\times 2^{E-127}$，可得真值=$(-1{)}^1\times (1.01{)}_2\times 2^{129-127}=-5.0$

（3）表示范围

IEEE 754单精度浮点型表示的最小绝对值和最大绝对值

• 最小绝对值：尾数全为0，阶码真值最小为-126，对应机器数为0000 0001，此时整体的真值为$(1.0{)}_2\times 2^{-126}$
• 最大绝对值：尾数全为1，阶码真值最小为-127，对应机器数为1111 1110，此时整体的真值为$(1.111....11{)}_2\times 2^{127}$

当然即便这样，还是有溢出的问题的，因此前面提到的阶码全0和全1就派上用途了。

• 当阶码全为0，尾数不全为0时，表示非规格化小数，也即$(+/-)(0.\times \times \times \times {)}_2\times 2^{-126}$，阶码的隐含最高位为0
• 当阶码全为0，尾数全为0时，表示真值正负0
• 当阶码全为1，尾数全为0时，表示无穷大（正负）
• 当阶码全为1，尾数不全为0时，表示非数值NaN（Not a Number），比如0/0