MATLAB基础语法之插值算法

Posted 2021-09-03 衾许°

•  无序标注为代码，使用时复制即可，如有不妥的注释，希望有大佬能指出。

分段三次埃尔米特插值

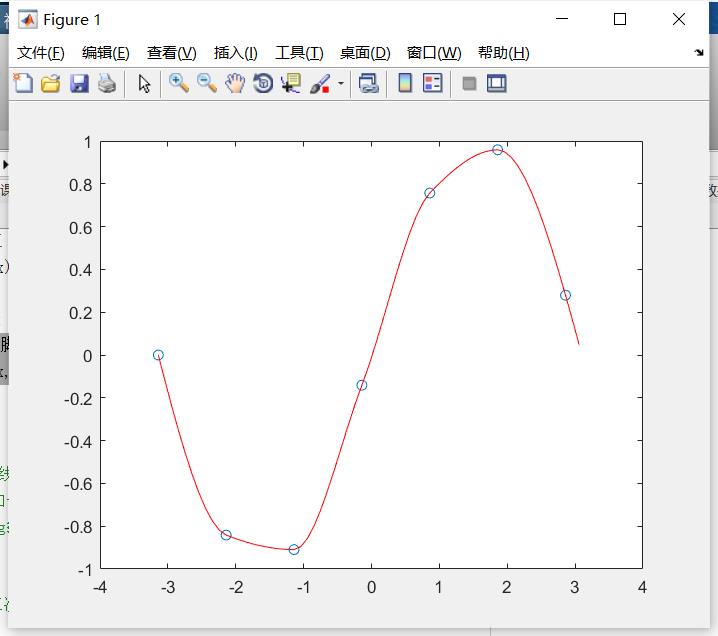
•  x = -pi:pi; y = sin(x);                 

%对自变量和因变量做定义，其中x以-pi为起点，pi为终点，1为步长生成一个等差数列

• new_x = -pi:0.1:pi;                     

%这里定义一个插入点等差数列，其内容为以-pi为起点，pi为终点，0.1位步长生成一个等差数列

• p = pchip(x,y,new_x);

%返回与 xq 中的查询点对应的插值 p 的向量。p 的值由 x 和 y 的保形分段三次插值确定。其实这一句我也不怎么理解，但我知道这个函数就是这么用的，主要是通过内置的函数方法来补全查询点处的插值，所以这里的p其实是一个模拟的new_y

• figure(1);

% 在同一个脚本文件里面，要想画多个图，需要给每个图编号，否则只会显示最后一个图

• plot(x, y, 'o', new_x, p, 'r-')

%朴实无华的画图函数，前面三个参数分别为段点的自变量和因变量以及这些点的描绘形式，后面三个参数则为插值点的自变量和因变量以及描绘形式，还是挺好理解的，是吧？

% 线方式： - 实线 :点线 -. 虚点线 - - 波折线 
% 点方式： . 圆点  +加号  * 星号  x x形  o 小圆
% 颜色： y黄； r红； g绿； b蓝； w白； k黑； m紫； c青

 三次样条插值和分段三次埃尔米特插值的对比

• x = -pi:pi; y = sin(x); 

%段点自变量和因变量的初始化

• new_x = -pi:0.1:pi;

%插值点自变量和因变量的初始化

• p1 = pchip(x,y,new_x);  

%分段三次埃尔米特插值

• p2 = spline(x,y,new_x);  

%三次样条插值

%从下图可以看出，这样条插值可以说很接近原本的sin(x)函数曲线了

• figure(2);
• plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')

• legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast')  

%标注显示在东南方向
% legend用法：
% LEGEND(string1,string2,string3, …)
% 分别将字符串1、字符串2、字符串3……标注到图中，每个字符串对应的图标为画图时的图标。
% ‘Location’用来指定标注显示的位置

n维数据的插值

• x = -pi:pi; y = sin(x); 

%段点自变量和因变量的初始化

• new_x = -pi:0.1:pi;

%插值点自变量和因变量的初始化

• p = interpn (x, y, new_x, 'spline');

%三次样条插值

% 等价于 p = spline(x, y, new_x);算是一种降低代码查重率的方式把

• figure(3);
• plot(x, y, 'o', new_x, p, 'r-')

人口预测实例

• population=[133126,133770,134413,135069,135738,136427,137122,137866,138639, 139538];
• year = 2009:2018;

%相当于是自变量和因变量的初始化

• p1 = pchip(year, population, 2019:2021)  

%分段三次埃尔米特插值预测

• p2 = spline(year, population, 2019:2021)

%三次样条插值预测
figure(4);
plot(year, population,'o',2019:2021,p1,'r*-',2019:2021,p2,'bx-')
legend('样本点','三次埃尔米特插值预测','三次样条插值预测','Location','SouthEast')

 看到这里，插值算法应该可以算是简单的了..以后的代码也会以这种方式呈现