拓扑排序详解

Posted 2021-09-03 C_YCBX Py_YYDS

文章目录

• • 拓扑排序之 Kahn 算法
  • • 视频详解
    • 算法限制
    • 时间复杂度
    • 空间复杂度
  • 以题代讲
  • • 视频详解题解
    • 解题代码

拓扑排序之 Kahn 算法

大家在上大学的时候，应该都遇到过这样的情况，有些高级的课程需要你先完成基础课程后才可以学习。在「图1. 课程关系图」中，如果你想选课程 C，那你需要先完成课程 B，如果你想选课程 B，那么你需要先完成课程 A。大学四年的课程还是非常多的，你总不希望等到大四了，想去修一门高级的课程，结果发现自己并没有完成基础课程，最终导致自己无法学习这门高级课程。那么你应当如何合理的安排自己的课程呢？如何才能理清课程关系呢？

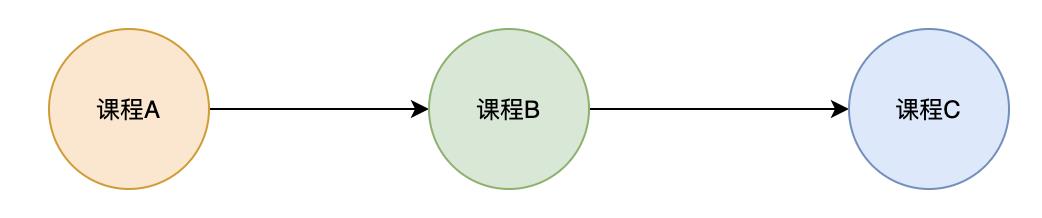
此时，就需要「拓扑排序」的帮忙了。「拓扑排序」针对的是 有向无环图 的一种算法。它是对「图」中所有顶点按照先后顺序的一种线性排序。换句话说，在如果存在顶点 u 和顶点 v，要想到达顶点 v，则必须要到达顶点 u 。那么在「拓扑排序」中，顶点 u 必须处于顶点 v 的前面。「拓扑排序」中最有名的算法当然是 Kahn 算法。

视频详解

视频链接

算法限制

「拓扑排序」针对的「图」的类型 必须同时 满足以下条件：

• 有向无环图；
• 「图」中至少有一个顶点「入度」为 0 。如果「图」中所有顶点都有「入度」，则代表所有顶点都至少有一个前置顶点，那么这个就没有顶点可以作为「拓扑排序」的起点。

时间复杂度

O (V+E)

V 表示顶点数，E 表示边数。

空间复杂度

O (V+E)

V 表示顶点数。

以题代讲

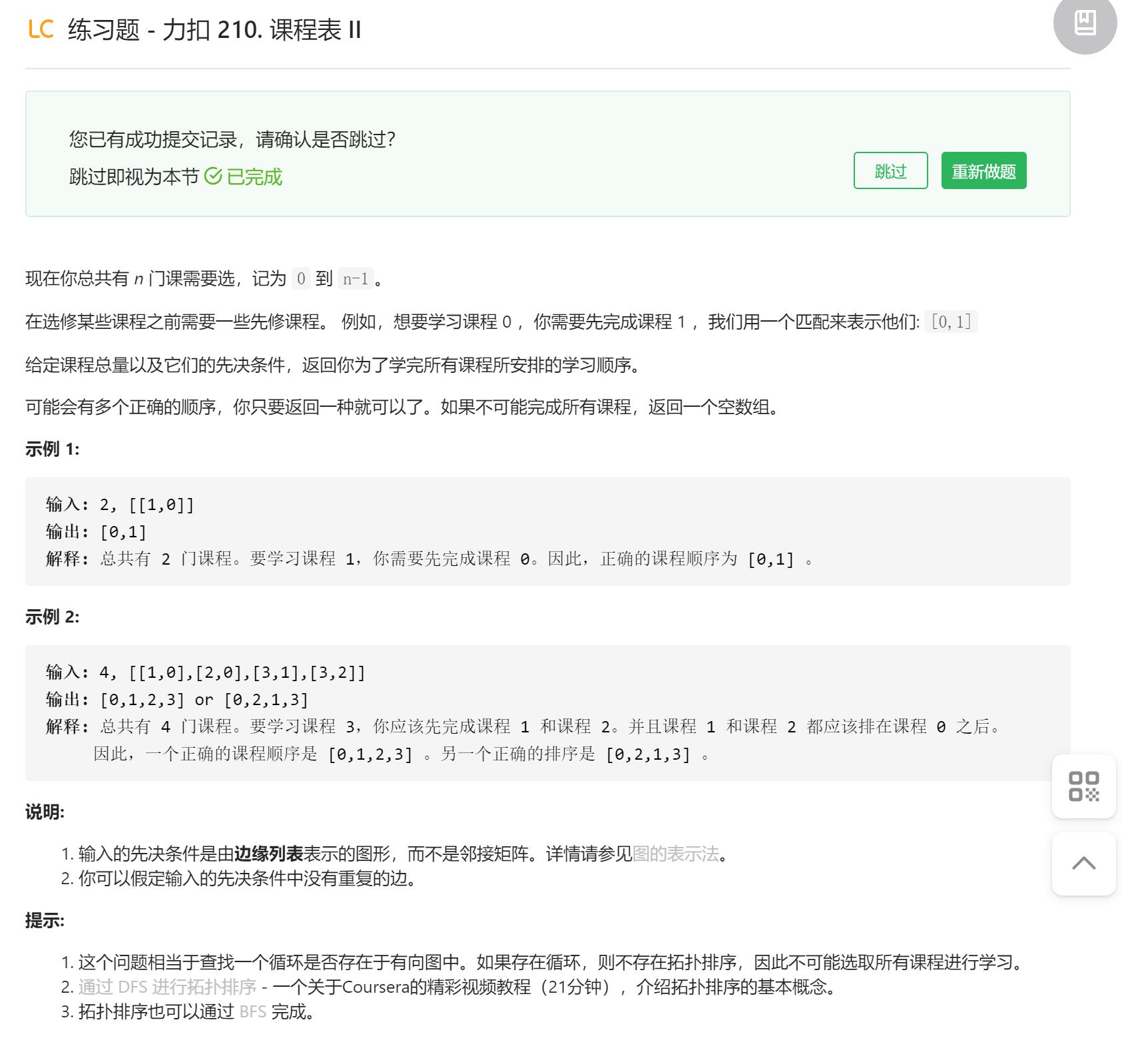
视频详解题解

视频链接

解题代码

class Solution {
    // Topo Sort
    public int[] findOrder(int numCourses, int[][] prerequisites) {
        int[] result = new int[numCourses];
        if(numCourses == 0){
            return result;
        }
        
        if(prerequisites == null || prerequisites.length == 0){
            for(int i = 0; i < numCourses; i++){
                result[i] = i;
            }
            return result;
        }
        
        int[] indegree = new int[numCourses];
        Queue<Integer> zeroDegree = new LinkedList<>();
        for(int[] pre : prerequisites){
            indegree[pre[0]]++;
        }
        for(int i = 0; i < indegree.length; i++){
            if(indegree[i] == 0){
                zeroDegree.add(i);
            }
        }
        if(zeroDegree.isEmpty()){
            return new int[0];
        }
        int index = 0;
        while( !zeroDegree.isEmpty() ){
            int course = zeroDegree.poll();
            result[index] = course;
            index++;
            for(int[] pre : prerequisites){
                if(pre[1] == course){
                    indegree[pre[0]]--;
                    if(indegree[pre[0]] == 0){
                        zeroDegree.add(pre[0]);
                    }
                }
            }
        }
        
        for(int in : indegree){
            if(in != 0){
                return new int[0];
            }
        }
        
        return result;
        
    }
}