CF1521D树转化为链的最小操作数

Posted 2021-09-03 hesorchen

题目

D. Nastia Plays with a Tree

给出一棵树，一次操作可以删一条边并且添加一条边。求将其转化为一条链的最小操作数，并给出一种具体方案。

解题思路

我们可以将$k$次操作的删边和添边分开来考虑，转化为先删$k$条边，再添$k$条边。最后要形成一条链，那么删$k$条边之后要保证形成的是若干子链，依次头尾相连即可。

问题就转化为了在树中删最少的边，形成若干链。

比较容易想到的是从一个叶节点出发，每遇到一个分叉就将其切断。但是类似于下面的情况（删除$2-4$、$3-6$），这样的操作数并不是最小的（可以只删除$2-3$）。

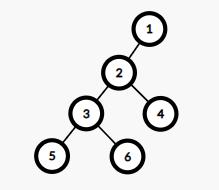
我们考虑一颗子树的情况。

1. 只有一个儿子结点。
   这时候不需要对其进行操作，已经是一条链。（也可以发现，当儿子节点数量$>=2$的时候，儿子节点数量越多，需要的花费就越大。下面会用到这个性质。）
2. 有两个儿子结点。
   结合上面给出的情况，有两种选择，第一种断开其与父亲的连边，第二种断开其中一个儿子的连边。两种操作单次花费相同、对子树的效果也相同（均可变成链），但是第一种操作中断开的其与父亲的连边，会使其父亲的儿子数量减少，这样可能会减少父亲的花费，因此选择第一种更优。
3. 有三个以上（k个）的儿子节点。
   也有两种选择，第一种断开其与父亲的连边，并且断开任意$k-2$个儿子的连边。第二种断开$k-1$个儿子的连边。与情况2同理，第一种选择可以减少父亲的儿子数量，更优。

代码

#include <bits/stdc++.h>
using namespace std;

const long long N = 1e5 + 5;

long long a[N];
long long col[N];

map<pair<int, int>, bool> remo;

vector<int> edge[N];
int degree[N];

vector<pair<int, int>> ADD;
vector<pair<int, int>> REMO;

void dfs(int u, int pre)
{
    int cnt = 0;
    vector<int> temp;
    for (auto v : edge[u])
    {
        if (v == pre)
            continue;
        dfs(v, u);
        if (!remo.count(make_pair(min(v, u), max(u, v)))) //统计儿子数量
            temp.emplace_back(v), ++cnt;
    }
    if (cnt >= 2)
    {
        remo[make_pair(min(pre, u), max(u, pre))] = 1;
        if (cnt >= 3)
            for (int i = 2; i < cnt; i++)
                remo[make_pair(min(temp[i], u), max(u, temp[i]))] = 1;
    }
}
int rt1, rt2;
bool vis[N];
void Dfs(int u, int pre)
{
    vis[u] = 1;
    int cnt = 0;
    for (auto v : edge[u])
    {
        if (v == pre || remo.count(make_pair(min(v, u), max(u, v))))
            continue;
        vis[v] = 1;
        Dfs(v, u);
        ++cnt;
    }
    if (cnt == 0)
    {
        if (rt1)
            rt2 = u;
        else
            rt1 = u;
    }
}
void init(int n)
{
    remo.clear();
    ADD.clear();
    REMO.clear();
    for (int i = 0; i <= n + 1; i++)
    {
        edge[i].clear();
        col[i] = degree[i] = vis[i] = 0;
    }
}
int main()
{
    cin.tie(nullptr);
    std::ios::sync_with_stdio(false);
    int t;
    cin >> t;
    while (t--)
    {
        int n;
        cin >> n;
        init(n);
        for (int i = 1; i < n; i++)
        {
            int u, v;
            cin >> u >> v;
            edge[u].emplace_back(v);
            edge[v].emplace_back(u);
            degree[u]++, degree[v]++;
        }
        int root = 0;
        for (int i = 1; i <= n; i++)
            if (degree[i] == 1 && !root)
                root = i;
        dfs(root, -1); //删边
        int pre = 0;
        for (int i = 1; i <= n; i++)
        {
            if (!vis[i])
            {
                rt1 = 0, rt2 = 0;
                Dfs(i, -1); //连边
                if (!rt2)
                    rt2 = i;
                if (pre)
                    ADD.emplace_back(make_pair(pre, rt1));
                pre = rt2;
            }
        }
        for (auto it : remo)
            REMO.emplace_back(make_pair(it.first.first, it.first.second));
        int len = remo.size();
        cout << len << endl;
        for (int i = 0; i < len; i++)
        {
            cout << REMO[i].first << ' ' << REMO[i].second << ' ';
            cout << ADD[i].first << ' ' << ADD[i].second << '\\n';
        }
    }
    return 0;
}