[PyTroch系列-9]：PyTorch基础 - 张量Tensor元素的统计运算

Posted 2021-09-03 文火冰糖的硅基工坊

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[PyTroch系列-9]：PyTorch基础 - 张量Tensor元素的统计运算相关的知识，希望对你有一定的参考价值。

作者主页(文火冰糖的硅基工坊)：https://blog.csdn.net/HiWangWenBing

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/119443802

第1章 Tensor运算概述

1.1 概述

1.3 “in place“运算

1.4 Tensor的广播机制: 不同维度的tensor实例运算

第1章 Tensor运算概述

1.1 概述

PyTorch提供了大量的张量运算，基本上可以对标Numpy多维数组的运算，以支持对张量的各种复杂的运算。

这些操作运算中大多是对数组中每个元素执行相同的函数运算，并获得每个元素函数运算的结果序列，这些序列生成一个新的同维度的数组。

https://www.runoob.com/numpy/numpy-linear-algebra.html

1.2 运算分类

（1）算术运算：加、减、系数乘、系数除

（2）函数运算：sin，cos

（3）取整运算：上取整、下取整

（4）统计运算：最大值、最小值、均值

（5）线性代数运算：矩阵、点乘、叉乘

1.3 “in place“运算

“in place“运算不是某个特定的函数运算，而是每个函数都有自己的“in place“运算的版本。

xxx_()：执行完该操作，直接修改tensor自身的值。

基本上，每个函数都有自己的in place版本。

如

torch.cos() =》torch.cos_()

torch.floor() =》torch.floor_()

1.4 Tensor的广播机制: 不同维度的tensor实例运算

1.5 环境准备

import numpy as np
import torch
 
print("Hello World")
print(torch.__version__)
print(torch.cuda.is_available())

1.6 统计运算概述

Torch提供了很多统计函数，用于从Tensor中查找最小元素，最大元素，百分位标准差和方差等

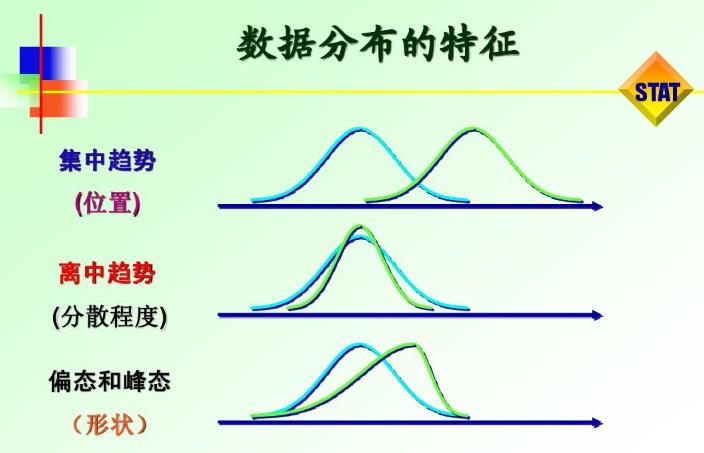
第1章平均值：mean

（1）原理概述

算术平均值是沿轴的元素的总和除以元素的数量。

算术平均值平均的前提是：求出所有带符号数值的总和。

简单算术平均公式：

设一组数据为X1，X2，...，Xn，简单的算术平均数的计算公式为：

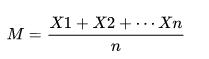
（2）函数使用说明

mean() 函数返回数组中元素的算术平均值。如果提供了轴，则沿其计算。

（3）案例

全统计

# 求所有元素的算术平均值

a = torch.Tensor([[1,2,3],[4,5,6]])  
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.mean(a)) 
print (a.mean()) 

print ('\\n')

输出：

源数据：
tensor([[1., 2., 3.],
        [4., 5., 6.]])


结果数据
tensor(3.5000)
tensor(3.5000)

按列统计（dim=0方向）

# 按列求算术平均值

a = torch.Tensor([[1,2,3],[4,5,6]])  
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.mean(a,dim=0)) 

print ('\\n')

输出：

源数据：
tensor([[1., 2., 3.],
        [4., 5., 6.]])


结果数据：
tensor([2.5000, 3.5000, 4.5000])

按行方向（dim=1）

# 按行求算术平均值

a = torch.Tensor([[1,2,3],[4,5,6]])  
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.mean(a,dim=1)) 

print ('\\n')

输出：

源数据：
tensor([[1., 2., 3.],
        [4., 5., 6.]])


结果数据：
tensor([2., 5.])

第2章汇总：sum

sum求出所有元素的算术和。

（1）全统计

# 求所有元素的算术和

a = torch.Tensor([[1,2,3],[4,5,6]])  
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.sum(a)) 
print (a.sum()) 

print ('\\n')

输出：

源数据：
tensor([[1., 2., 3.],
        [4., 5., 6.]])


结果数据：
tensor(21.)
tensor(21.)

（2）按列统计（按照dim=0方向）

# 求所有元素的算术和

a = torch.Tensor([[1,2,3],[4,5,6]])  
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.sum(a,dim=0)) 
print (a.sum(dim=0)) 

print ('\\n')

输出：

源数据：
tensor([[1., 2., 3.],
        [4., 5., 6.]])


结果数据：
tensor([5., 7., 9.])
tensor([5., 7., 9.])

（3）按行统计（按照dim=1方向）

# 求所有元素的算术和

a = torch.Tensor([[1,2,3],[4,5,6]])  
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.sum(a,dim=1)) 
print (a.sum(dim=1)) 

print ('\\n')

输出：

源数据：
tensor([[1., 2., 3.],
        [4., 5., 6.]])


结果数据：
tensor([ 6., 15.])
tensor([ 6., 15.])

第3章积：prod

prod()函数用来计算所有元素的乘积。

输出：

源数据：
tensor([[1., 2., 3.],
        [4., 5., 6.]])


结果数据：
tensor(720.)
tensor(720.)

输出结果：

源数据：

tensor([[1., 2., 3.],
        [4., 5., 6.]])


结果数据：
tensor(720.)
tensor(720.)

第4章最大值：max

max（）找出所有元素中，算术值最大的数值。

# 求所有元素的最大值

a = torch.Tensor([[1,2,3],[4,5,6]])  
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.max(a)) 
print (a.max()) 

print ('\\n')

源数据：
tensor([[1., 2., 3.],
        [4., 5., 6.]])


结果数据：
tensor(6.)
tensor(6.)

第5章最小值：min

min（）找出所有元素中，算术值最小的数值。

# 求所有元素的最小值

a = torch.Tensor([[1,2,3],[4,5,6]])  
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.min(a)) 
print (a.min()) 

print ('\\n')

输出：

源数据：
tensor([[1., 2., 3.],
        [4., 5., 6.]])


结果数据：
tensor(1.)
tensor(1.)

第6章最大值索引：argmax

argmax求所有元素中最大值的索引,index从0开始，线性排列。

# 求所有元素中最大值的索引,index从0开始，线性排列

a = torch.Tensor([[1,2,3,4],[5,6,7,8]])  
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.argmax(a)) 
print (a.argmax())

输出：

源数据：
tensor([[1., 2., 3., 4.],
        [5., 6., 7., 8.]])


结果数据：
tensor(7)
tensor(7)

最7章最小值索引：argmin

# 求所有元素中最小值的索引,index从0开始，线性排列

a = torch.Tensor([[1,2,3,4],[5,6,7,8]])   
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.argmin(a)) 
print (a.argmin())

输出：

源数据：
tensor([[1., 2., 3., 4.],
        [5., 6., 7., 8.]])


结果数据：
tensor(0)
tensor(0)

第8章算术平均值：median

# 求所有元素中的中间值索引

a = torch.Tensor([[4,3,2,1],[8,7,6,5]])   
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.median(a)) 
print (a.median())

输出：

源数据：
tensor([[4., 3., 2., 1.],
        [8., 7., 6., 5.]])


结果数据：
tensor(4.)
tensor(4.)

第9章众数值：mode

众数（Mode）是指在统计分布上具有明显集中趋势点的数值，代表数据的一般水平。也是一组数据中出现次数最多的数值，有时众数在一组数中有好几个。

众数是样本观测值在频数分布表中频数最多的那一组的组中值，主要应用于大面积普查研究之中。

众数是在一组数据中,出现次数最多的数据，是一组数据中的原数据，而不是相应的次数。

一组数据中的众数不止一个，如数据2、3、-1、2、1、3中，2、3都出现了两次，它们都是这组数据中的众数。

一般来说，一组数据中，出现次数最多的数就叫这组数据的众数。

例如：1，2，3，3，4的众数是3。

# 求每个维度中的众数值

a = torch.Tensor([[1,1,2,1,0,4],[7,7,7,6,6,1]])   
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.mode(a))

输出：

源数据：
tensor([[1., 1., 2., 1., 0., 4.],
        [7., 7., 7., 6., 6., 1.]])


结果数据：
torch.return_types.mode(
values=tensor([1., 7.]),
indices=tensor([3, 2]))

备注：是两维度的数据：

第一个维度是数值values序列，指明源张量中，每个维度序列中的众数值。

第二个维度是索引indices序列，指明源张量中，众数值在序列中最大的index位置。

上图中，第一个维度的序列中，众数值是1，众数在序列中的最大的index为3.

上图中，第二个维度的序列中，众数值是7，众数在序列中的最大的index为2

第10章标准方差：std

（1）理论概述

标准差是一组数据离平均值的分散程度的一种度量。

标准差（Standard Deviation），是离均差平方的算术平均数（即：方差）的算术平方根，用σ表示。

标准差也被称为标准偏差，或者实验标准差，在概率统计中最常使用作为统计分布程度上的测量依据。

在实验中单次测量总是难免会产生误差，为此我们经常测量多次，然后用测量值的平均值表示测量的量，并用误差条来表征数据的分布，其中误差条的高度为±标准误差。这里即标准差。

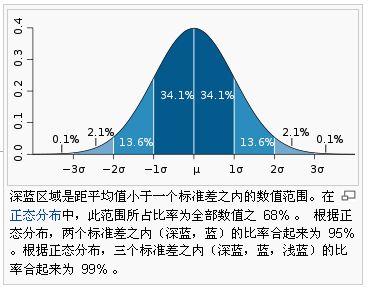
如果数组是 [1，2，3，4]，则其平均值为 2.5。因此，差的平方是 [2.25,0.25,0.25,2.25]，并且再求其平均值的平方根除以 4，即 sqrt(5/4) ，结果为 1.1180339887498949。

# 求所有元素的标准差

a = torch.Tensor([[1,2,3,4,5],[-1,-2,-3,-4,-5]])   
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print(torch.mean(a))  #均值
print (torch.std(a))  #标准差

输出:

源数据：
tensor([[ 1.,  2.,  3.,  4.,  5.],
        [-1., -2., -3., -4., -5.]])


结果数据：
tensor(0.)
tensor(3.4960)

第11章方差：var

（1）概述

统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数，即 mean((x - x.mean())** 2)。 #mean：求平均

换句话说，标准差是方差的平方根

（2）方差与标准方差的关系：

备注：正态分布使用的是标准方差，而不是方差。

# 求所有元素的方差

a = torch.Tensor([[1,2,3,4,5],[-1,-2,-3,-4,-5]])   
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print(torch.mean(a))  #均值
print (torch.var(a))  #方差
print (torch.sqrt(torch.var(a)))  #方差的平方根
print (torch.std(a))  #标准差

输出：

源数据：
tensor([[ 1.,  2.,  3.,  4.,  5.],
        [-1., -2., -3., -4., -5.]])


结果数据：
tensor(0.)
tensor(12.2222)
tensor(3.4960)
tensor(3.4960)

第12章频度：bincount

bincount求你所有元素出现的次数

# 求每个维度中的频度

a = torch.tensor([1,1,2,1,20,4,2,4,5,6,3,2,1])   
print ("源数据：")
print (a)
print ('\\n')


print ("结果数据：")
print (torch.bincount(a))

输出：

源数据：
tensor([ 1,  1,  2,  1, 20,  4,  2,  4,  5,  6,  3,  2,  1])


结果数据：
tensor([0, 4, 3, 1, 2, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1])

备注：

（1）目前只支持整数序列，这与其输出格式是整数索引有关。

（2）输出结果是一个从最小值0到最大值的统计列表，这里的最大值是20.

数字0：出现次数为0.

数字1：出现次数为4

数字2：出现次数为3

数值3：出现次数为1

数字4：出现次数为2

数字5：出现次数为1

数字6：出现次数为1

数字7-19：出现次数为0

数字20：出现次数为1