(d2l-ai/d2l-zh)《动手学深度学习》pytorch 笔记前言(介绍各种机器学习问题)以及数据操作预备知识Ⅰ
Posted Dontla
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了(d2l-ai/d2l-zh)《动手学深度学习》pytorch 笔记前言(介绍各种机器学习问题)以及数据操作预备知识Ⅰ相关的知识,希望对你有一定的参考价值。
笔记基于2021年7月26日发布的版本,书及代码下载地址在github网页的最下面
(d2l-ai/d2l-zh)《动手学深度学习》pytorch 笔记(1)(序言、pytorch的安装、神经网络涉及符号)
文章目录
- 1、前言(35)
- 2、预备知识(57)
1、前言(35)
1.1 ⽇常⽣活中的机器学习(36)
数据集(dataset)(36)
参数(parameter)
最佳参数集
模型(model)
模型族:通过操作参数而生成的所有不同程序(输入-输出映射)的集合
学习算法(learning algorithm):使用数据集来选择参数的元程序
学习(learning):模型的训练过程(37)通过这个过程,我们可以发现正确
的参数集,从而从使模型强制执行所需的行为。换句话说,我们用数据训练(train)我们的模型。
训练过程通常包含如下步骤:(37)
- 从一个随机初始化参数的模型开始,这个模型基本毫不”智能“。
- 获取⼀些数据样本(例如,音频片段以及对应的{是,否}标签)。
- 调整参数,使模型在这些样本中表现得更好。
- 重复第2步和第3步,直到模型在任务中的表现令你满意。

1.2 关键组件(37)
- 我们可以学习的数据(data)。
- 如何转换数据的模型(model)。
- 一个目标函数(objective function),用来量化模型的有效性。
- 调整模型参数以优化目标函数的算法。
1.2.1 数据(38)
样本(example) & 数据点(data point) & 数据实例(data instance)
独立同分布(independently and identically distributed, i.i.d.)
通常每个样本由⼀组称为特征(features,或协变量(covariates))的属性组成。
在监督学习问题中,要预测的是一个特殊的属性,它被称为标签(label,或目标(target))
当每个样本的特征类别数量都是相同的,所以其特征向量是固定长度的,这个长度被称为数据的维数(dimensionality)固定长度的特征向量是一个方便的属性,它有助于我们量化学习大量样本。(38)
与传统机器学习方法相比,深度学习的一个主要优势是可以处理不同长度的数据。
1.2.2 模型(39)
深度学习与经典方法的区别主要在于:前者关注的功能强大的模型,这些模型由神经网络错综复杂的交织在⼀起,包含层层数据转换,因此被称为深度学习(deep learning)。
1.2.3 目标函数(39)
在机器学习中,我们需要定义模型的优劣程度的度量,这个度量在⼤多数情况是“可优化”的,我们称之为目标函数(objective function)
损失函数(loss function, 或cost function)
当任务为试图预测数值时,最常见的损失函数是平方误差(squared error),即预测值与实际值之差的平方
当试图解决分类问题时,最常⻅的⽬标函数是最小化错误率,即预测与实际情况不符的样本⽐例
通常,损失函数是根据模型参数定义的,并取决于数据集。在⼀个数据集上,我们通过最小化总损失来学习模型参数的最佳值。该数据集由⼀些为训练而收集的样本组成,称为训练数据集(training dataset,或称为训练集(training set))。然而,在训练数据上表现良好的模型,并不⼀定在“新数据集“上有同样的效能,这⾥的“新数据集“通常称为测试数据集(test dataset,或称为测试集(test set))。
数据集分成两部分:训练数据集⽤于拟合模型参数,测试数据集⽤于评估拟合的模型
当⼀个模型在训练集上表现良好,但不能推⼴到测试集时,我们说这个模型是“过拟合”(overfitting)的
1.2.4 优化算法(39)
⼀旦我们获得了⼀些数据源及其表⽰、⼀个模型和⼀个合适的损失函数,我们接下来就需要⼀种算法,它能够搜索出最佳参数,以最小化损失函数。深度学习中,大多流⾏的优化算法通常基于⼀种基本⽅法‒梯度下降(gradient descent)。
1.3 各种机器学习问题(40)
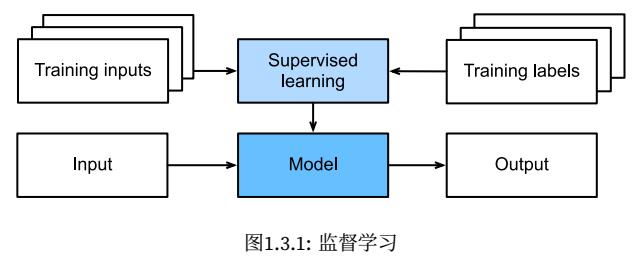
1.3.1 监督学习(40)
监督学习(supervised learning)擅⻓在“给定输⼊特征”的情况下预测标签。每个“特征-标签”对都称为⼀个样本(example)。
在⼯业中,⼤部分机器学习的成功应⽤都是监督学习。这是因为在⼀定程度上,许多重要的任务可以清晰地描述为:在给定⼀组特定的可⽤数据的情况下,估计未知事物的概率。
回归(regression)(41)
回归(regression)是最简单的监督学习任务之⼀。
判断回归问题的⼀个很好的经验法则是,任何有关“多少”的问题很可能就是回归问题。⽐如:
• 这个⼿术需要多少小时?
• 在未来六小时,这个镇会有多少降⾬量?
⾼斯噪声(41)
分类(classification)(41)
分类(classification)问题。在分类问题中,我们希望模型能够预测样本属于哪个类别(category,正式称为类(class))。
最简单的分类问题是只有两类,我们称之为“⼆元分类”。
当我们有两个以上的类别时,我们把这个问题称为多类分类(multiclass classification)问题。
与解决回归问题不同,分类问题的常⻅损失函数被称为交叉熵
(cross-entropy)。
有⼀些分类任务的变体可以⽤于寻找层次结构,层次结构假定在许多类之间存在某种关系。因此,并不是所有的错误都是均等的。我们宁愿错误地分⼊⼀个相关的类别,也不愿错误地分⼊⼀个遥远的类别,这通常被称为层次分类(hierarchical classification)。
标记问题(43)
学习预测不相互排斥的类别的问题称为多标签分类(multilabel classification)。
搜索(44)
有时,我们不仅仅希望输出为⼀个类别或⼀个实值。在信息检索领域,我们希望对⼀组项⽬进⾏排序。
该问题的⼀种可能的解决⽅案:⾸先为集合中的每个元素分配相应的相关性分数,然后检索评级最⾼的元素。
推荐系统(recommender system)(44)
另⼀类与搜索和排名相关的问题是推荐系统(recommender system),它的⽬标是向给特定⽤⼾进⾏“个性化”推荐。
反馈循环(45)啥意思?
序列学习(45)
与时间相关的,如病人状况监测、视频帧序列、文字序列、语音序列
序列学习需要摄取输入序列或预测输出序列,或两者兼而有之。具体来说,输⼊和输出都是可变⻓度的序列,例如机器翻译和从语⾳中转录⽂本。
标记和解析 token&parser(46)Ent(entity)
自动语⾳识别(46)
文本到语音(46)
机器翻译(46)
困难在于不同语言之间的语法差异
其他序列学习应⽤(46)
确定“⽤⼾阅读⽹⻚的顺序”是⼆维布局分析问题。
对话问题:确定下⼀轮对话,需要考虑对话历史状态以及现实世界的知识
1.3.2 ⽆监督学习(unsupervised learning)(47)
数据中不含有“⽬标”的机器学习问题为⽆监督学习(unsupervised learning)
• 聚类(clustering)问题:没有标签的情况下,给数据分类
• 主成分分析(principal component analysis)问题:找到少量的参数来准确地捕捉数据的线性相关属性
• 因果关系(causality)和概率图模型(probabilistic graphical models)问题:描述观察到的许多数据的根本原因
• ⽣成对抗性⽹络(generative adversarial networks):提供⼀种合成数据的⽅法,甚⾄像图像和音频这样复杂的结构化数据;检查真实和虚假数据是否相同
1.3.3 与环境互动(47)
学习是在算法与环境断开后进⾏的,被称为离线学习(offline learning)

离线学习缺点是,解决的问题相当有限。与预测不同,“与真实环境互动”实际上会影响环境。
环境变化:当训练和测试数据不同时数据分布偏移(distribution shift)的问题
1.3.4 强化学习(reinforcement learning)(48)
使⽤机器学习开发与环境交互并采取⾏动
涉及领域:机器⼈、对话系统,甚⾄开发视频游戏的⼈⼯智能(AI)。
深度强化学习(deep reinforcement learning)将深度学习应⽤于强化学习的问题
举例:深度Q⽹络(Q-network)、AlphaGo 程序
在强化学习问题中,agent 在⼀系列的时间步骤上与环境交互。在每个特定时间点,agent 从环境接收⼀些观察(observation),并且必须选择⼀个动作(action),然后通过某种机制(有时称为执⾏器)将其传输回环境,最后 agent 从环境中获得 奖励(reward)。此后新⼀轮循环开始,agent 接收后续观察,并选择后续操作,依此类推。
强化学习的⽬标是产⽣⼀个好的策略(policy)。强化学习 agent 的选择的”动作“受策略控制,即⼀个从环境观察映射到⾏动的功能。

任何监督学习问题都能转化为强化学习问题(49)
环境甚⾄可能不会告诉我们是哪些⾏为导致了奖励(49)
强化学习者必须处理学分分配(credit assignment)问题:决定哪些⾏为是值得奖励的,哪些⾏为是需要惩罚的(49)
强化学习可能还必须处理部分可观测性问题。(49)(看不懂啥意思@)
当环境可被完全观察到时,我们将强化学习问题称为⻢尔可夫决策过程(markov decision process)。当状态不依赖于之前的操作时,我们称该问题为上下⽂赌博机(contextual bandit problem)。当没有状态,只有⼀组最初未知回报的可⽤动作时,这个问题就是经典的多臂赌博机(multi-armed bandit problem)。
1.4 起源(50)
最小均⽅算法
估计(estimation)(50)
修剪均值估计(50)
神经⽹络(neural networks)核心:
• 线性和⾮线性处理单元的交替,通常称为层(layers)。
• 使⽤链式规则(也称为反向传播(backpropagation))⼀次性调整⽹络中的全部参数。
1.5 深度学习之路(51)
一些帮助研究⼈员在过去⼗年中取得巨⼤进步的想法:(52)
• 新的容量控制⽅法,如dropout [Srivastava et al., 2014],有助于减轻过拟合的危险。这是通过在整个神经⽹络中应⽤噪声注⼊ [Bishop, 1995] 来实现的,出于训练⽬的,⽤随机变量来代替权重。
• 注意⼒机制解决了困扰统计学⼀个多世纪的问题:如何在不增加可学习参数的情况下增加系统的记忆和复杂性。研究⼈员通过使⽤只能被视为可学习的指针结构 [Bahdanau et al., 2014] 找到了⼀个优雅的解决⽅案。不需要记住整个⽂本序列(例如⽤于固定维度表⽰中的机器翻译),所有需要存储的都是指向
翻译过程的中间状态的指针。这⼤⼤提⾼了⻓序列的准确性,因为模型在开始⽣成新序列之前不再需要记住整个序列。
• 多阶段设计。例如,存储器⽹络[Sukhbaatar et al., 2015] 和神经编程器-解释器 [Reed & DeFreitas, 2015]。它们允许统计建模者描述⽤于推理的迭代⽅法。这些⼯具允许重复修改深度神经⽹络的内部状态,从而执⾏推理链中的后续步骤,类似于处理器如何修改⽤于计算的存储器。
• 另⼀个关键的发展是⽣成对抗⽹络 [Goodfellow et al., 2014] 的发明。传统模型中,密度估计和⽣成模型的统计⽅法侧重于找到合适的概率分布和(通常是近似的)抽样算法。因此,这些算法在很⼤程度上受到统计模型固有灵活性的限制。⽣成式对抗性⽹络的关键创新是⽤具有可微参数的任意算法代替采样器。然后对这些数据进⾏调整,使得鉴别器(实际上是对两个样本的测试)不能区分假数据和真实数据。通过使⽤任意算法⽣成数据的能⼒,它为各种技术打开了密度估计的⼤⻔。驰骋的斑⻢ [Zhu et al., 2017]和假名⼈脸 [Karras et al., 2017] 的例⼦都证明了这⼀进展。即使是业余的涂鸦者也可以根据描述场景
布局的草图⽣成照⽚级真实图像([Park et al., 2019] )。
• 在许多情况下,单个GPU不⾜以处理可⽤于训练的⼤量数据。在过去的⼗年中,构建并行和分布式训练算法的能⼒有了显著提⾼。设计可伸缩算法的关键挑战之⼀是深度学习优化的主⼒——随机梯度下降,它依赖于相对较小的小批量数据来处理。同时,小批量限制了GPU的效率。因此,在1024个GPU上进⾏训练,例如每批32个图像的小批量⼤小相当于总计约32000个图像的小批量。最近的⼯作,⾸先是由[Li, 2017] 完成的,随后是 [You et al., 2017] 和 [Jia et al., 2018] ,将观察⼤小提⾼到64000个,将ResNet50模型在Imagenet数据集上的训练时间减少到不到7分钟。作为⽐较——最初的训练时间是按天为单位
的。
• 并⾏计算的能⼒也对强化学习的进步做出了相当关键的贡献。这导致了计算机在围棋、雅达⾥游戏、星际争霸和物理模拟(例如,使⽤MuJoCo)中实现超⼈性能的重⼤进步。有关如何在AlphaGo中实现这⼀点的说明,请参⻅如 [Silver et al., 2016] 。简而⾔之,如果有⼤量的(状态、动作、奖励)三元组可⽤,即只要有可能尝试很多东西来了解它们之间的关系,强化学习就会发挥最好的作⽤。仿真提供了这样⼀条途径。
• 深度学习框架在传播思想⽅⾯发挥了⾄关重要的作⽤。允许轻松建模的第⼀代框架包括Caffe25、Torch26和Theano27。许多开创性的论⽂都是⽤这些⼯具写的。到⽬前为⽌,它们已经被TensorFlow28(通常通过其⾼级API Keras29使⽤)、CNTK30、Caffe 231和Apache MXNet32所取代。第三代⼯具,即⽤
于深度学习的命令式⼯具,可以说是由Chainer33率先推出的,它使⽤类似于Python NumPy的语法来描述模型。这个想法被PyTorch34、MXNet的Gluon API35和Jax36都采纳了。
1.6 成功案例(53)
• 智能助理
• 数字助理
• 物体识别
• 游戏 状态空间(54)
• ⾃动驾驶
人⼯智能奇点(54)
1.7 特点(55)
表⽰学习的⽬的是寻找表⽰本⾝,因此深度学习可以称为“多级表⽰学习”。(55)
深度学习⽅法中最显著的共同点是使⽤端到端训练。也就是说,与其基于单独调整的组件组装系统,不如构建系统,然后联合调整它们的性能。
端到端

深度学习的⼀个关键优势是它不仅取代了传统学习管道末端的浅层模型,而且还取代了劳动密集型的特征⼯程过程。此外,通过取代⼤部分特定领域的预处理,深度学习消除了以前分隔计算机视觉、语⾳识别、⾃然语⾔处理、医学信息学和其他应⽤领域的许多界限,为解决各种问题提供了⼀套统⼀的⼯具。(55)
以牺牲可解释性为代价(55)
接受次优解(55)
1.8 小结(56)
• 机器学习研究计算机系统如何利⽤经验(通常是数据)来提⾼特定任务的性能。它结合了统计学、数据挖掘和优化的思想。通常,它被⽤作实现⼈⼯智能解决⽅案的⼀种⼿段。
• 表⽰学习作为机器学习的⼀类,其研究的重点是如何⾃动找到合适的数据表⽰⽅式。深度学习是通过学习多层次的转换来进⾏的多层次的表⽰学习。
• 深度学习不仅取代了传统机器学习的浅层模型,而且取代了劳动密集型的特征⼯程。
• 最近在深度学习⽅⾯取得的许多进展,⼤都是由廉价传感器和互联⽹规模应⽤所产⽣的⼤量数据,以及(通过GPU)算⼒的突破来触发的。
• 整个系统优化是获得⾼性能的关键环节。有效的深度学习框架的开源使得这⼀点的设计和实现变得⾮常容易。
1.9 练习(56)
2、预备知识(57)
2.1 数据操作(58)
张量(tensor):绍n维数组(58)
与普通numpy ndarray相比,张量类很好地⽀持GPU加速计算,支持自动微分
2.1.1 入门(58)
具有⼀个轴的张量对应数学上的向量(vector)
具有两个轴的张量对应数学上的 矩阵(matrix)
具有两个轴以上的张量没有特殊的数学名称
张量中的每个值都称为张量的元素(element)
行向量arange,形状shape,元素个数numel,修改形状reshape
# -*- coding: utf-8 -*-
"""
@File : begin.py
@Time : 2021/8/5 14:59
@Author : Dontla
@Email : sxana@qq.com
@Software: PyCharm
"""
import torch
# 行向量
x = torch.arange(12)
print(x) # tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
# 形状
print(x.shape) # torch.Size([12])
# 元素个数(number of element)
print(x.numel()) # 12
# 修改形状(-1 自动推导)
# X = x.reshape(3, 4)
# X = x.reshape(-1, 4)
X = x.reshape(3, -1)
print(X)
# tensor([[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11]])
全0张量zeros和全1张量ones:
# -*- coding: utf-8 -*-
"""
@File : begin.py
@Time : 2021/8/5 14:59
@Author : Dontla
@Email : sxana@qq.com
@Software: PyCharm
"""
import torch
# 全0张量
x = torch.zeros((2, 3, 4))
print(x)
# tensor([[[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]],
#
# [[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]]])
# 全1张量
x = torch.ones((2, 3, 4))
print(x)
# tensor([[[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]],
#
# [[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]]])
randn 初始化网络参数值,均值为0、标准差为1的标准⾼斯(正态)分布中随机采样
import torch
# 初始化网络参数值,均值为0、标准差为1的标准⾼斯(正态)分布中随机采样
x = torch.randn(3, 4)
print(x)
# tensor([[-0.8740, -1.5099, -0.2514, 0.5912],
# [-0.7873, 0.6065, 0.6698, -0.2849],
# [-1.4781, -0.4106, -0.2990, -0.5989]])
tensor 直接分别为张量每个元素指定值
import torch
# 直接分别为张量每个元素指定值
x = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(x)
# tensor([[2, 1, 4, 3],
# [1, 2, 3, 4],
# [4, 3, 2, 1]])
2.1.2 运算(60)
按元素(elementwise)操作:将标准标量运算符应⽤于数组的每个元素。对于将两个数组作为输⼊的函数,按元素运算将⼆元运算符应⽤于两个数组中的每对位置对应的元素。我们可以基于任何从标量到标量的函数来创建按元素函数。(啥意思??)
一维张量和差积商幂
import torch
X = torch.tensor([1.0, 2, 4, 8])
Y = torch.tensor([2, 2, 2, 2])
print(X + Y) # tensor([ 3., 4., 6., 10.])
print(X - Y) # tensor([-1., 0., 2., 6.])
print(X * Y) # tensor([ 2., 4., 8., 16.])
print(X / Y) # tensor([0.5000, 1.0000, 2.0000, 4.0000])
print(X ** Y) # tensor([ 1., 4., 16., 64.])
一维张量自然指数e的幂 exp
import torch
x = torch.tensor([1.0, 2, 4, 8])
print(torch.exp(x)) # tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])
张量 连结 cat(concatenate)
dim为轴,最外层为0,次外层为1,以此类推
import torch
X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(torch.cat((X, Y), dim=0))
# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [ 2., 1., 4., 3.],
# [ 1., 2., 3., 4.],
# [ 4., 3., 2., 1.]])
print(torch.cat((X, Y), dim=1))
# tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],
# [ 4., 5., 6., 7., 1., 2., 3., 4.],
# [ 8., 9., 10., 11., 4., 3., 2., 1.]])
逻辑判断True、False 逐个对比张量中的元素 ==
import torch
X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(X == Y)
# tensor([[False, True, False, True],
# [False, False, False, False],
# [False, False, False, False]])
对张量中所有元素求和 sum
import torch
X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(X.sum()) # tensor(66.)
2.1.3 广播机制(broadcasting mechanism)(自动匹配形状)(62)
import torch
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
print(a)
# tensor([[0],
# [1],
# [2]])
print(b)
# tensor([[0, 1]])
print(a + b)
# tensor([[0, 1],
# [1, 2],
# [2, 3]])
由于 a 和 b 分别是 3 × 1 和 1 × 2 矩阵,如果我们让它们相加,它们的形状不匹配。我们将两个矩阵⼴播为⼀个更⼤的 3 × 2 矩阵,如下所⽰:矩阵 a将复制列,矩阵 b将复制⾏,然后再按元素相加。
2.1.4 索引和切片(63)
- 利用索引和切片获取张量中指定(范围)元素的值
-1表示倒数第一个元素,1:3表示下标为1、2的元素
import torch
X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
print(X)
# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.]])
print(X[-1])
# tensor([ 8., 9., 10., 11.])
print(X[1:3])
# tensor([[ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.]])
- 利用索引或切片为张量元素赋值
import torch
X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
print(X)
# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.]])
X[1, 2] = 9
print(X)
# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 9., 7.],
# [ 8., 9., 10., 11.]])
X[0:2, :] = 12
print(X)
# tensor([[12., 12., 12., 12.],
# [12., 12., 12., 12.],
# [ 8., 9., 10., 11.]])
X[0:2, :] = torch.tensor([[11, 11, 11, 11], [11, 12, 13, 14]])
print(X)
# tensor([[11., 11., 11., 11.],
# [11., 12., 13., 14.],
# [ 8., 9., 10., 11.]])
2.1.5 节省内存(张量内存使用规范)(63)
张量计算中使用Y = X + Y,将为Y开辟新的内存空间,频繁开辟内存空间将降低运行效率;同时如果Y作为神经网络的参数时,如果使用多线程,这样的赋值有可能使调用对象引用到未更新的参数,导致错漏
验证:
import torch
X = torch.tensor([1.0, 2, 4, 8])
Y = torch.tensor([2, 2, 2, 2])
before = id(Y)
Y = Y + X
new = id(Y)
print(before) # 2112489973184
print(new) # 2112489973248
解决办法:(切⽚表⽰法)
感受一下使用切片与不使用切片的区别
import torch
X = torch.tensor([1.0, 2, 4, 8])
Y = torch.tensor([2, 2, 2, 2])
Z = torch.zeros_like(Y)
print('id(Z):', id(Z)) # id(Z): 2362931341056
Z[:] = X + Y
print('id(Z):', id(Z)) # id(Z): 2362931341056
Z = X + Y
print('id(Z):', id(Z)) # id(Z): 2561881336640
当然,如果使用相同参数的时间跨度比参数更新的时间跨度短,那么用切片表示法给参数变量自己更新也是可以的,如:
注意用Y += X的时候,数据类型要一致,否则会报错
import torch
X = torch.tensor([1.0, 2, 4, 8])
Y = torch.tensor([2., 2, 2, 2])
before = id(Y)
Y[:] = Y + X
# 或者
# Y += X
new = id(Y)
print(before) # 2112489973184
print(new) # 2112489973248
2.1.6 转换为其他 Python 对象(64)
转换为 NumPy 张量很容易,反之也很容易。转换后的结果不共享内存。这个小的不便实际上是⾮常重要的:
当你在 CPU 或 GPU 上执⾏操作的时候,如果 Python 的 NumPy 包也希望使⽤相同的内存块执⾏其他操作,你不希望停下计算来等它。
作者的意思是说,这个功能是非常有用的!你可以让cpu或gpu处于一直计算中,
import torch
X 以上是关于(d2l-ai/d2l-zh)《动手学深度学习》pytorch 笔记前言(介绍各种机器学习问题)以及数据操作预备知识Ⅰ的主要内容,如果未能解决你的问题,请参考以下文章