采用递归与迭代法思想，分别用java编程去实现欧几里德，斐波那契，牛顿迭代法

Posted 2021-09-03 阿啄debugIT

前言​

数学中的欧几里德算法，斐波那契数列和牛顿迭代法求非线性方程的近视解，同时用递归与迭代法分别去实现！

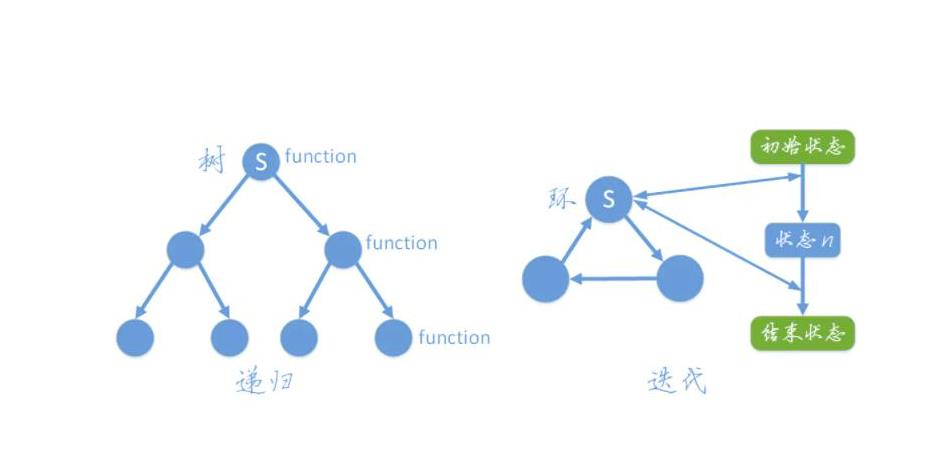
1，循环（loop），指的是在满足条件的情况下，重复执行同一段代码。比如，while语句。   循环则技能对应集合，列表，数组等，也能对执行代码进行操作。
2，迭代（iterate），指的是按照某种顺序逐个访问列表中的每一项。比如，for语句。  　　迭代只能对应集合，列表，数组等。不能对执行代码进行迭代。
3，遍历（traversal），指的是按照一定的规则访问树形结构中的每个节点，而且每个节点都只访问一次。   遍历同迭代一样，也不能对执行代码进行遍历。
4，递归（recursion），指的是一个函数不断调用自身的行为。比如，以编程方式输出著名的斐波纳契数列。
　　　　(1)，通俗的解释：递归就像往存钱罐里存钱，先往里边塞钱，2块，5块，10块这样的塞，叫入栈。取钱的时候，后塞进去的先取出来，这叫出栈。具体多少钱，要全部出栈才知道。  
　　　　(2)，递归分类：线性递归和尾递归。

递归法——《盗梦空间》

递归，就是在运行的过程中调用自己，每次旨在缩小问题规模。
构成递归需具备的条件：
1. 子问题须与原始问题为同样的事，且更为简单；
2. 不能无限制地调用本身，须有个出口，化简为非递归状况处理。

迭代法——《明日边缘》

迭代法也称辗转法，是一种不断用变量的旧值递推新值的过程。

迭代是自己执行很多次，每次旨在更接近目标。

1.欧几里德算法，典型的迭代法

最经典的迭代算法，用于计算两个整数a,b的最大公约数。

假如需要求 1997 和 615 两个正整数的最大公约数,用欧几里得算法，是这样进行的：

以除数和余数反复做除法运算，当余数为 0 时，取当前算式除数为最大公约数，所以就得出了 1997 和 615 的最大公约数 1。

java代码实现算法： 

package com.azdebugit.suanfa.test.diedai;

public class ZuiDaGongYue {
    public static int gcd(int a, int b) {

        if (a <= 0 || b <= 0) {//预防错误
            return 0;
        }
        int temp;
        if (a < b) { //交换a,b保证a大于b
            temp = a;
            a = b;
            b = a;
        }
        //迭代计算
        while (b > 0) {  //边界条件
            temp = a % b;
            a = b;
            b = temp;
        }
        return a;//最大公约数
    }

    public static void main(String[] args) {
        System.out.println(gcd(128,28));
    }
}

欧几里得算法应用

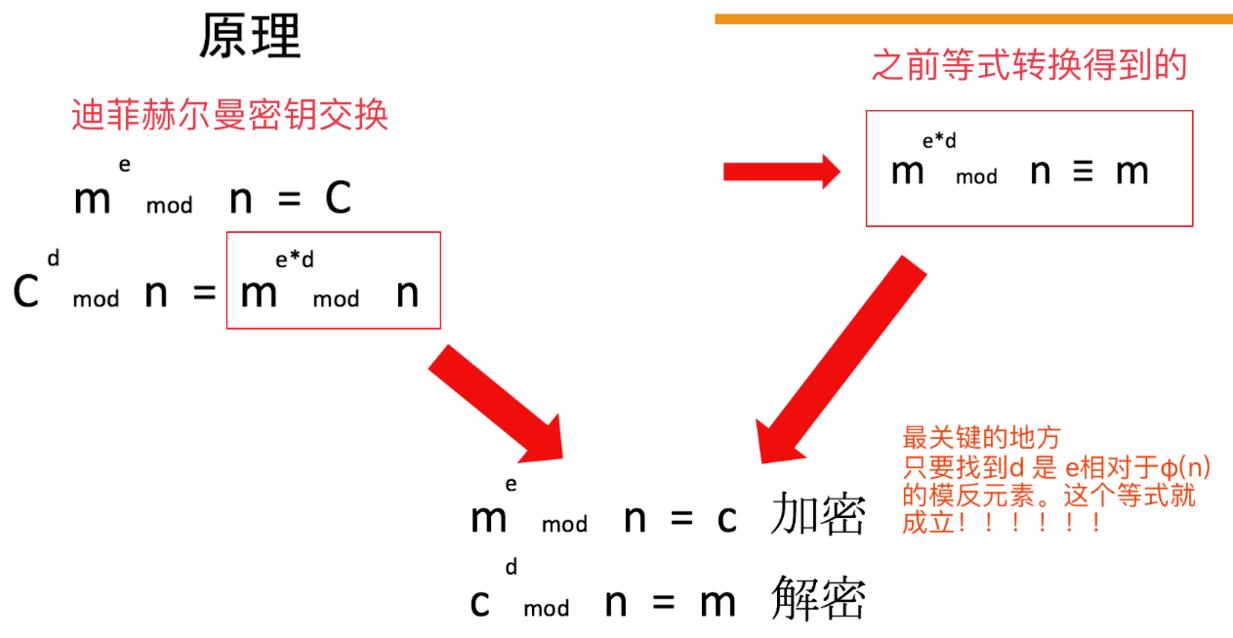
RSA是第一个也是使用的最广泛的公钥加密算法，在1978年由R.Rivest、AdiShamir和Adleman三人发明，并以他们的名字命名。RSA算法的安全性基于大数因子分解的困难性，下面介绍一下它的基本原理：

 2.斐波那契数列

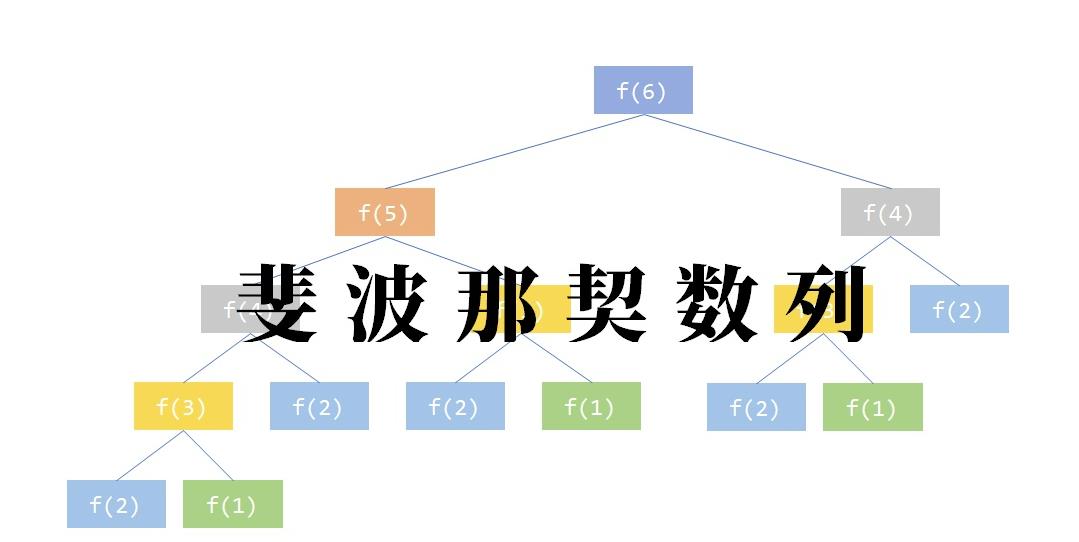
斐波纳契数列，又称黄金分割数列。

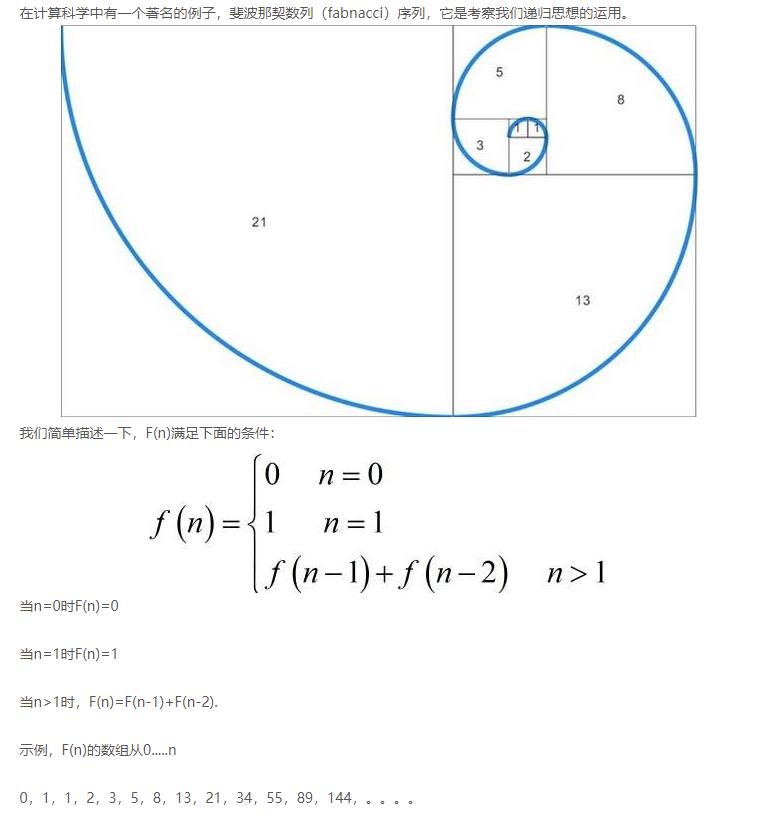
大学计算机课程中算法讲解中一个经典的数列计算。可以通过递归和非递归实现。
代码递归实现：

package com.azdebugit.suanfa.test.digui;

import org.springframework.util.StopWatch;

public class FiboTest {
    public static int fib(int n) {
        //边界判断
        if (n < 1) {
            return 0;
        }
        if (n == 1 || n == 2) {
            return 1;
        }

        return fib(n - 1) + fib(n - 2);
    }

//    代码非递归实现：

    public static int fib1(int n) {
        //边界判断
        if (n < 1) {
            return 0;
        }
        if (n == 1 || n == 2) {
            return 1;
        }
        int f1 = 1, f2 = 1, fn = 0;
        int i;
        for (i = 3; i <= n; i++) {//迭代计算
            fn = f1 + f2;
            f1 = f2;
            f2 = fn;
        }
        return fn;
    }

    public static void main(String[] args) {
        StopWatch s1 = new StopWatch();
        System.out.print("--递归实现--"+fib(50)+"----");
        System.out.println(s1.getTotalTimeMillis());
        StopWatch s2 = new StopWatch();
        System.out.print("--非递归实现--"+fib1(50)+"----");
        System.out.println(s2.getTotalTimeMillis());
    }
}

   3.牛顿迭代法

牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x) = 0的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛。

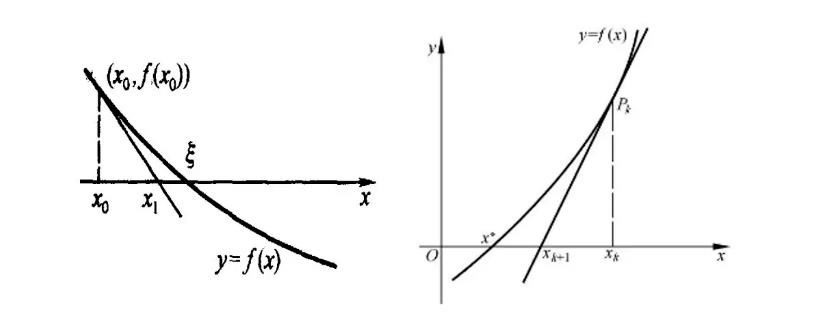该方法广泛用于计算机编程中。牛顿迭代关系式 

 

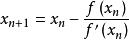
代码实现：

public class NewtonIterator {

    public static void main(String[] args) {
        double x = 10,precision = 0.000000001;
        int maxcyc = 100;
        NewtonIterator newtonIterator = new NewtonIterator();
        if(newtonIterator.newton(x, precision, maxcyc) == 1){
            System.out.println("该值附近的根为" + result + " 迭代次数 ： " + num);
        }else{
            System.out.println("迭代失败！");
        }
    }

    private static double result;
    private static int num;

    public double func(double x){ //函数
        return x*x*x*x - 3*x*x*x + 1.5*x*x - 4.0;
    }

    public double func1(double x){//导数
        return 4*x*x*x - 9*x*x + 3*x;
    }

    public int newton(double x, double precision,int maxcyc){//迭代次数

        double x1,x0;
        int k;
        x0 = x;

        for(k = 0; k < maxcyc; k++){
            if (func1(x0) == 0.0) {
                System.out.println("迭代过程中导数为0！");
                return 0;
            }

            x1 = x0 - func(x0) / func1(x0);  //牛顿迭代计算关系式，x1是是曲线过点(x0,f(x0))做切线，相交于x轴上的横坐标
            if (Math.abs(x1-x0) < precision || Math.abs(func(x1)) < precision) {//精度判断，达到精度就结束迭代
                result = x1;
                num = k + 1;
                return 1;
            }else{
                x0 = x1;
            }
        }

        System.out.println("迭代次数超过预期!");
        return 0;
    }
}

计算结果

该值附近的根为2.648936536183 迭代次数 ： 10

​