论文解读 WWW2019｜基于开放数据的因果推断：社区环境特征如何影响居民健康？

Posted 2021-09-03 Akashi2021

        本篇文章是解读顶会论文的第一篇，为了追求阅读效率，省略了本人认为不影响理解的内容，并非论文的全部中文翻译，主要包括文章的核心内容和方法，想要看包含文献综述等完整论文内容的小伙伴可以自己阅读英文原文哦～

文章标题《Understanding the Effects of the Neighbourhood Built Environment on Public Health with Open Data》

       本文发表于2019年CCF-A类顶会WWW，由剑桥大学的学者提出，是关于因果推断，社会科学和计量经济学的论文，属于交叉学科研究方向。关于CV，NLP，RecSys等方向的顶会论文解读已有不少大佬总结，关注计量经济学和社会科学方面的顶会论文相对较少。这篇论文比较有意思，因此简要介绍帮助大家快速了解文章核心。

废话不多说，我们开始吧≡ω≡

1. 文章背景

        在公共政策以及社会科学的领域中，研究社区环境对居民健康的影响是一个较为典型的、有价值的方向。传统的研究方法以社会调研为主，其时间和空间跨度是有限的，这会导致时间和空间上的粗粒度数据（如面板数据），且大规模的社会调研会导致较高的人力物力成本，通常来说是效率很低的做法。基于此，本文利用开放数据（如OSM等项目提供的数据），在较细的时空粒度以及因果关系框架的基础上，提出了一种将邻里社区特征对居民健康的影响联系起来的方法。具体而言，作者使用因果推断等方法，研究了三年内伦敦600多个区域的运动场所对抗抑郁药处方流行率的影响，将其作为一个典型案例来证明社区环境对居民健康的影响。这种方法有很多好处，看到后面你就知道了╰(￣▽￣)╭。

2. 研究方法 

        先介绍总体方法：文章关注的是社区环境的具体特征，如某些特定服务的存在（体育设施）对人口健康的outcome（如抗抑郁药处方）的影响。这里的社区环境特征被称为treatment。这里采取了因果推理的观点（假设你已经了解因果推理相关概念），文章想找到对于社区环境施加体育设施这种treatment会给人口健康结果带来的因果效应，简单来说就是，我们需要评估，当体育设施这个具体特征改变的时候，它对于人口健康结果（如抗抑郁药处方）有什么样的影响。

2.1 研究单位

       在因果推理中，实验对象叫做unit，可以是一个或者多个，在本文中可以看作是施加了treatment的研究单位，即不同的neighbourhoods，具体就是伦敦的625个行政选区（ward)。在一年开始时，每个区域都被视为施加了特定单位量的treatment。

2.2 Matching

      在介绍matching方法之前，我们要了解一个基础的因果推理方法叫做随机对照实验（RCT，randomized controlled trials），如果应用这种方法，本文的做法理论上应该是随机选择一半的区域（ward），将没有施加treatment的区域集合作为对照组（control group)，剩下的作为实验组（treatment group）。但是显而易见这种方法是非常拉垮的，毕竟我们不能随心所欲地控制在哪个区域去施加treatment。

        虽然RCT的方法是不可取的，但它背后的思想非常有价值。它确保了除treatment变量的所有影响outcome的变量都是平衡的，这意味着两组对象的实验结果在treatment status上是可比的，因为treatment是唯一的区别所在。

        那么问题来了——怎样找到一个alternative method来实现RCT的思想呢？

       本文采用的是因果推理中的匹配算法（Matching Procedure）。这里要介绍一个概念叫混杂变量（confounder），它是影响treatment或outcome（包括同时影响）的变量（类似于计量经济学中的协变量）。我们构建对照组和实验组时需使confounders平衡，而treatment的分配随机。匹配的过程可以概括如下：对每个对照组的unit，在实验组中找到confounders都相同的unit作为一个match，即精确匹配（Exact Matching）。（你问为什么要这么做？——请查阅因果推理相关资料，这里不做赘述）然而想要找到精确匹配并不是always possible，因此我们退而求其次，对于每个对照组的unit，在实验组中找到confounders变量平均值差异最小的unit就行了。

2.3 Propensity Score

       大致了解了匹配的思路后，我们需要解决两个问题：1.怎样最小化match中confounders的差异？2.怎样最大化match中treatment的dose值？（dose为文中体育设施的单位量）

       对于第一个问题，解决方法是使用一个指标来量化match中confounders之间的差异，这个指标就是倾向评分（propensity score）；对于第二个问题，文章将0-1二分的treament变量改为multiple treatment levels。

3. 论文图示

4. Matching with Binary Treatment

        为了后续更好地说明multiple treatment的情况，这里先介绍二分匹配。最常用的一种匹配方法是最近邻匹配法（nearest neighbor matching），其匹配过程可以概括如下：设为配对的units集合，​​​​​​​为confounders集合，​​​​​​​为单一confounder，优化的目的是最小化配对units的距离（distance）：

        其中，代表unit 的第个confounder。

        该优化问题可看作一个图匹配问题（gragh matching problem），给定一个二分图，在​​​​​​​的一个子图中，的边集中任意两条边都不依附于同一个顶点，则称是一个匹配。若一个图的某个匹配中，图的所有顶点都是匹配点，则称该匹配为完美匹配。一个图的所有匹配中，所含匹配边数最大的匹配称为最大匹配。使所有边权和最小的最大匹配叫做最优加权图匹配。在本文中，每个confounder都有不同的权重，因此可以看作是寻找最优加权图匹配的问题。

5. Matching with Multiple Treatment Levels

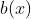        假设代表施加treatment的等级，我们先前的讨论是基于​​​​​​​的取值仅为0或1的情况，然而对于本文的特定情况，我们必须考虑将其扩展到有许多可能的treatment level的情况。在这种存在multiple treatment levels的情况下，基于倾向评分的匹配仍然需要平衡观察到的混杂变量confounders，即满足下列条件：，其中表示每个unit属于treatment的倾向性（预测概率），表示confounders，为倾向评分。

        倾向评分的估计是一个典型的建模问题，方法有许多种，最常见的就是线性回归模型，也有学者使用机器学习模型，如 LR + LightGBM。由于我们的因变量treatment是多分类的情况，本文使用的模型是ordered logistic model：

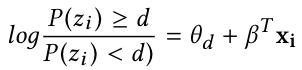
       其中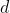， 为施加treatment的dose值，可取值。注意：在此处，给定confounders的treatment level分布仅取决于，估计倾向评分就等于估计。这里可使用最大似然法进行该参数的估计，表示为。

       上述的工作主要是为了使confounders平衡，除此之外还需要使配对units的treatment level差异最大化。假设unit 和 unit 的距离为，目标为最小化该距离：

       其中，为一个极小正数， 为防止出现confounders完全相同的配对units。该问题是一个最优非二分匹配问题，我们现在可以构建一个图，每个顶点代表一个unit，边连接到其他unit，边上的权重为。使用Edmonds算法（Edmonds' non-bipartite matching algorithm）可以在多项式时间内解决在非二分图中寻找最大匹配的问题。我们可以使用Edmonds算法得到一个最佳匹配M，并用和分别表示outcome和treatment，然后通过以下公式计算平均因果效应（Average Treatment Effect，简称 ATE）：

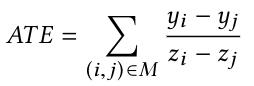
 6. 数据集和变量

6.1 Confounding Variables

       混杂变量可分为三类。首先是人口结构。伦敦和许多发达城市一样，是一个商业活跃的地区，城市的不同部分吸引着生活在不同阶段的人们。这里将人口分为0-15岁（儿童）、16-64岁（工作年龄）和64岁以上（退休）的人群。其次，一个地区全职和兼职员工的数量有助于我们确定该地区是住宅区还是商业区，这会影响体育设施和抗抑郁药处方的数量。

        第二是绿地的可用性。尽管伦敦是地球上最具绿色的首都之一，但在绿地的可用性方面还是有很大差异。人口统计数据集通过两个值来描述这个特征，即% area that is green space和% homes with deficient access to nature。接触大自然不仅与心理健康相关，而且也决定了可用的体育场地的类型。

       最后，confounders还包括一些贫困措施（Deprivation），如表所示：

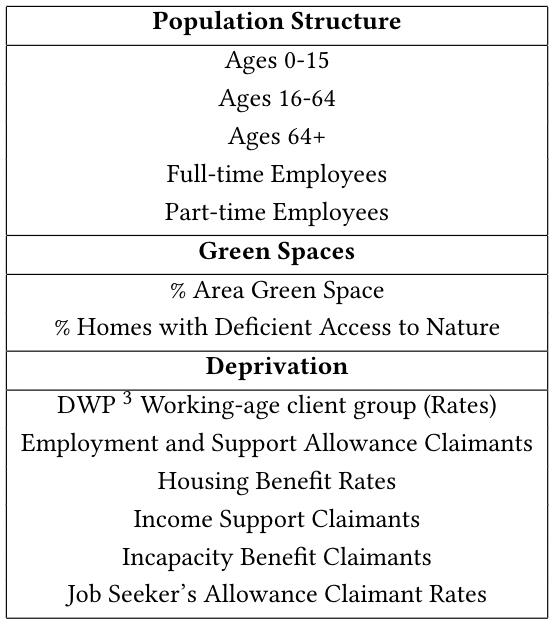
 6.2 The Treatment Effect

        用体育设施代表treatment，包括一系列体育相关的场馆，如下表所示。涉及到的场馆及其频率用词云表示。本文的treatment level为1,2,3,4四个等级。

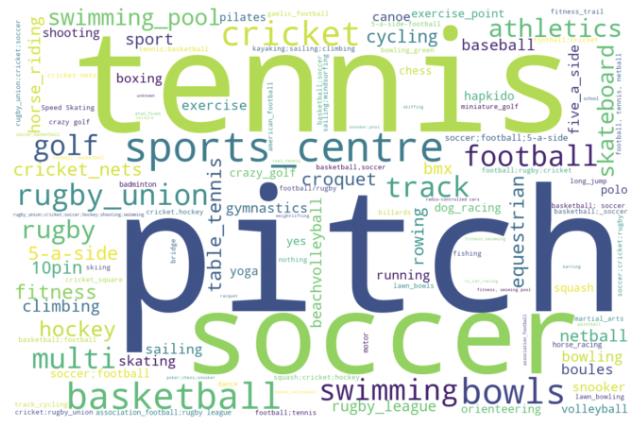
 7. ATE结果

        确定了数据集和变量后，使用前面提到的方法计算因果效应。这里的units是在伦敦的单位区域（ward）内，单位个人（per person）抗抑郁药处方的变化和单位（per dosage）运动场地。从实验结果可以看到2011～2013三年的ATE都是负数。这表明了treatment对outcome有负面的影响。如果我们将其与在null model上match的treatment效应分布进行比较（每个ward的运动场地计数是随机的），如图所示，这也表明存在负方向的影响。

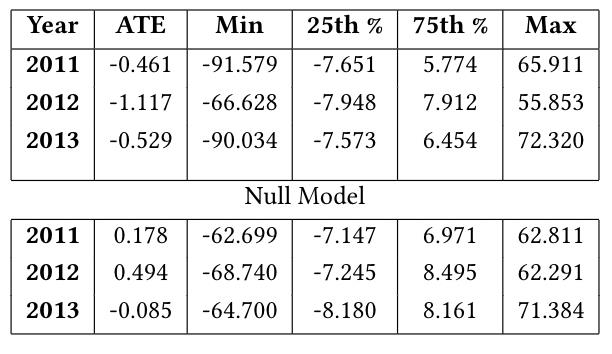
 8. 评估因果效应的可靠性

        由于我们没有可比较的“真实”效应，因此在这种情况下，匹配算法的有效性使用三个指标进行评估：dose差异、confounders平衡性、匹配程序在生成数据集上的性能。

8.1 Dose Difference

        下图显示了三年内每对配对units的dose分布。行表示该对中treatment水平较高的unit，列表示treatment水平较低的unit。深色表示该dose水平的配对数量更多。

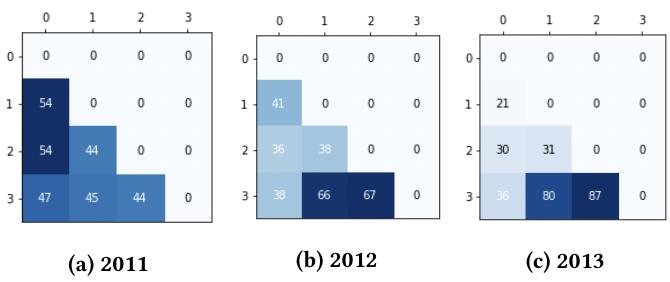
8.2 Confounder Balance

       下表显示了配对的high dose unit 和 low dose unit之间confounders的平均值。

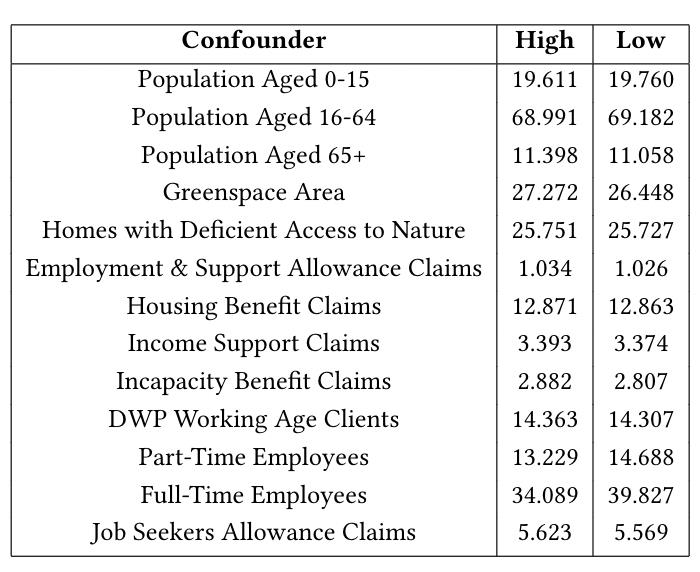
       在这里可以看到，大多数confounders在两组之间成功地平衡了。例外情况可能是标准化的全职和兼职员工比率，其差异分别超过5%和1.4%。文中深入探讨了这两个变量非平衡性产生的原因，大致是由于伦敦三大商业区的因素，由于其特殊性，不能简单地当作误差处理，否则会导致其他confounders的非平衡性增加。

8.3 匹配生成数据

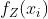       假设需要生成个units,。每个unit都具有个confounders（这里具体为13个），表示为。首先，我们使用截断正态分布（truncated normal distribution）建模，先为所有units生成confounders的值，然后使用指数分布（exponential distribution）建模生成每个unit的treatment值，即。最后，仍然使用截断正态分布建模，生成每个unit的outcome值，即（具体公式请参考原文）。下图为标准化后的生成数据和真实数据分布对比图：

       在生成数据集上运行与真实数据集相同的匹配算法。文中共生成6250个units，每批625个,具有不同的混杂因素集，设置四个ATE真值，倒推出数据，使用匹配算法计算四次求ATE值。根据匹配算法计算的treatment effects如表所示：

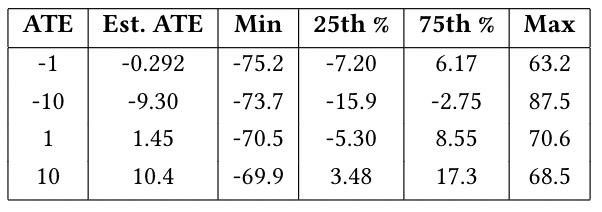
       表中第一列是作者设定的真实ATE值。在这里，我们可以看到与真实的treatment effects类似的结果，若设定较大的ATE值，该匹配算法能够达到更好的估计效果。如果真实的ATE值较小，则因果推断的效应不太准确。这说明了我们应该如何解释从实际数据中获得的结果，由于前面在真实数据集上计算出的对于outcome的因果效应很小，我们应该更倾向于保守的解释（可以看出论文是非常严谨的）。 

9 后续讨论

       文章后续讨论了confounder的选取及其影响，以及一些可能的误差来源以及假设问题。综上，文章通过研究体育场馆的可用性在多大程度上对伦敦周边地区抗抑郁药处方起着因果作用，为解决社会和公共政策问题提供了一个数据驱动的方法。

       ok，本文的介绍到此结束，学经济学的朋友们应该感觉特别轻松，关于省略的部分推荐大家阅读英文原文：https://dl.acm.org/doi/10.1145/3308558.3313701，有相关问题也欢迎感兴趣的朋友和我探讨。