最大正方/矩/菱形

Posted 2023-03-01 佐鼬Jun

最大正方形

题解链接: link.

最大矩形

题目链接: link 或者挑程白书P360

题意：

给定$H\times W$个边长为$1$的正方形瓷砖，$1$代表损坏,$0$完好，现在问由完好瓷砖构成的最大长方形的面积

思路：

题意与最大正方形差不多，但是如果以及依旧定义$f(i,j)$为以右下角$(i,j)$为向左上方扩展形成的最大长方形的面积,那就不好转移方程，因为$f(i,j)$是不受限于$f(i-1,j)$,$f(i-,j-1)$,$f(i,j-1)$的最小面积的，举一个简单的例子

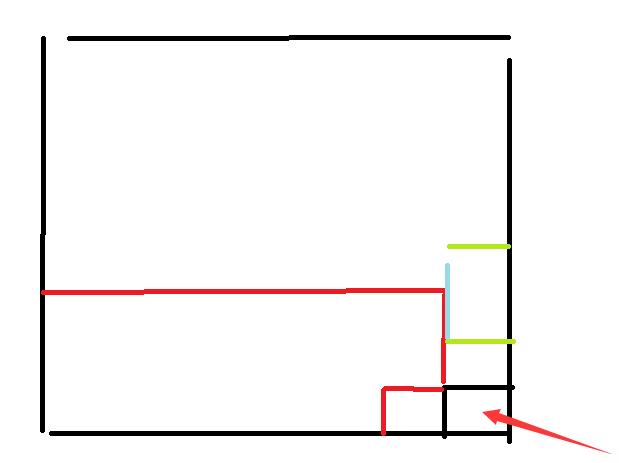
右下角为$(i,j)$，很明显$f(i,j)$与$f(i-1,j)和$f(i,j-1)$$f(i-1,j-1)$的最小面积，并没有直接联系，所以不好转移。
根据直方图的最大矩形面积的这个题，发现只需要处理出每行的每个点的最大高度，就可以把这个题就变成了对每行算一遍直方图的最大矩形即可，时间复杂度为$O(HW)$

#include <bits/stdc++.h>
using namespace std;
const int N = 2000;
#define ll long long
int n, m;
int g[N][N];
int h[N][N];
int l[N], sta[N], r[N];
int GetArea(int h[]) 
    h[0] = -1, h[m + 1] = -1;
    int tt = -1;
    sta[++tt] = 0;
    for (int i = 1; i <= m; i++) 
        while (h[sta[tt]] >= h[i]) 
            tt--;
        
        l[i] = i - sta[tt];
        sta[++tt] = i;
    

    tt = -1;
    sta[++tt] = m + 1;
    for (int i = m; i >= 1; i--) 
        while (h[sta[tt]] >= h[i]) 
            tt--;
        
        r[i] = sta[tt] - i;
        sta[++tt] = i;
    
    int res = 0;
    for (int i = 1; i <= m; i++) 
        res = max(res, h[i] * (l[i] + r[i] - 1));
    
    return res;

int main() 
    cin >> n >> m;
    for (int i = 1; i <= n; i++) 
        for (int j = 1; j <= m; j++) 
            cin >> g[i][j];
        
    

    int res = 0;

    for (int i = 1; i <= n; i++) 
        for (int j = 1; j <= m; j++) 
            if (g[i][j] == 0) 
                h[i][j] = h[i - 1][j] + 1;
            
        

        res = max(GetArea(h[i]), res);
    
    cout << res << endl;
    return 0;

最大菱形(最大正方形变形)

链接: link

题意：

给定一个$N\times M$的字符串矩阵，现在问图中有多少个同字母组成的菱形？(详情看题目)

思路：

设$f(i,j)$为菱形最下角时，菱形的最大长度。那么此时这个值，就依靠$f(i-1,j-1),f(i-1,j),f(i-1,j+1),f(i-2,j)$，在这些位置处的字母与当前位置字母相同时，就可以发现
$f(i,j)=min(f(i-1,j-1),f(i-1,j),f(i-1,j+1),f(i-2,j))+1$
是可以去掉$f(i-1,j)$的，因为有$f(i-1,j-1),f(i-1,j+1),f(i-2,j)$，这就相当于三个方向延伸的最小值，也就是当前这个点向上方能延伸的最大边长
如果字母不同或者越界，那就说明延伸不了，那就直接$f(i,j)=1$,即当前位置当作一个菱形
此时把所有情况都累加，就是所有菱形的数目

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 2e3 + 10;
const int inf = 2e9;
#define ll long long
char g[N][N];
int f[N][N];
int n, m;

int main() 
    cin >> n >> m;
    for (int i = 1; i <= n; i++) 
        scanf("%s", g[i] + 1);
    
    int res = 0;
    for (int i = 1; i <= n; i++) 
        for (int j = 1; j <= m; j++) 
            f[i][j] = 1;
            if (i >= 3 && j >= 2 && j <= m - 1 && g[i][j] == g[i - 1][j - 1] &&
                g[i][j] == g[i - 1][j] && g[i][j] == g[i - 1][j + 1] &&
                g[i][j] == g[i - 2][j]) 
                f[i][j] += min(f[i - 1][j - 1], f[i - 1][j], f[i - 1][j + 1],
                                f[i - 2][j]);
            
            res += f[i][j];
        
    
    cout << res << endl;

To be continued
如果你有任何建议或者批评和补充，请留言指出，不胜感激