luogu5490POJ1151模板扫描线 /Atlantis (求矩形面积并)
Posted 小哈里
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了luogu5490POJ1151模板扫描线 /Atlantis (求矩形面积并)相关的知识,希望对你有一定的参考价值。
Problem
Atlantis
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 33064 Accepted: 11454
Description
There are several ancient Greek texts that contain descriptions of the fabled island Atlantis. Some of these texts even include maps of parts of the island. But unfortunately, these maps describe different regions of Atlantis. Your friend Bill has to know the total area for which maps exist. You (unwisely) volunteered to write a program that calculates this quantity.
Input
The input consists of several test cases. Each test case starts with a line containing a single integer n (1 <= n <= 100) of available maps. The n following lines describe one map each. Each of these lines contains four numbers x1;y1;x2;y2 (0 <= x1 < x2 <= 100000;0 <= y1 < y2 <= 100000), not necessarily integers. The values (x1; y1) and (x2;y2) are the coordinates of the top-left resp. bottom-right corner of the mapped area.
The input file is terminated by a line containing a single 0. Don’t process it.
Output
For each test case, your program should output one section. The first line of each section must be “Test case #k”, where k is the number of the test case (starting with 1). The second one must be “Total explored area: a”, where a is the total explored area (i.e. the area of the union of all rectangles in this test case), printed exact to two digits to the right of the decimal point.
Output a blank line after each test case.
Sample Input
2
10 10 20 20
15 15 25 25.5
0
Sample Output
Test case #1
Total explored area: 180.00
Source
Mid-Central European Regional Contest 2000
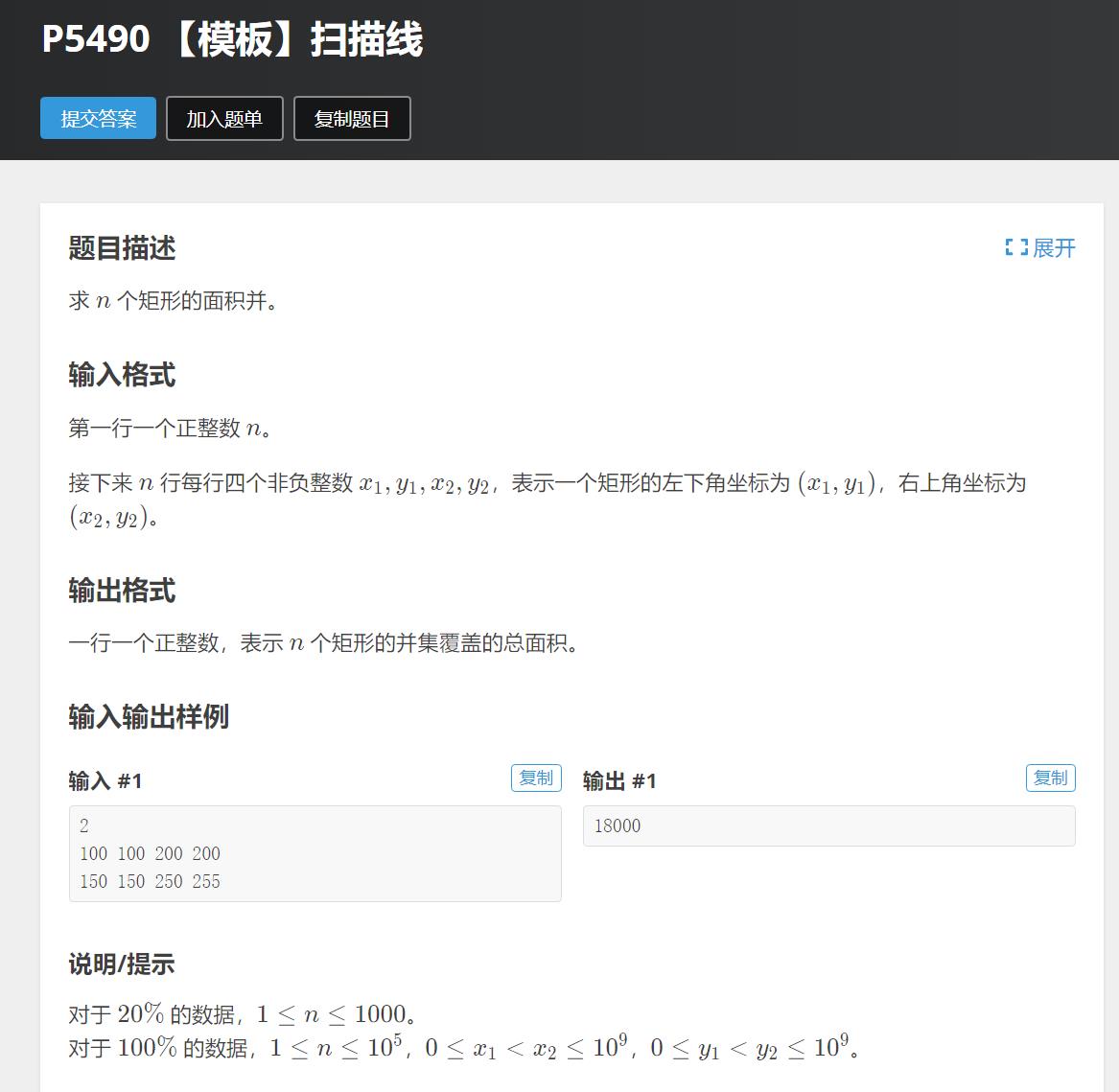
solution
-
扫描线:假设有一条扫描线从一个图形的下方扫向上方(或者左方扫到右方),那么通过分析扫描线被图形截得的线段就能获得所要的结果。该过程可以用线段树(维护区间信息)进行加速。
-
求矩形面积并:矩形的面积简化为 ∑ 截线段长度×扫过的高度。
- 对于扫过的高度只需要将直线存起来按照高度h从下到上排序,每次的 (line[i+1].h-line[i].h) 就是扫过的高度。
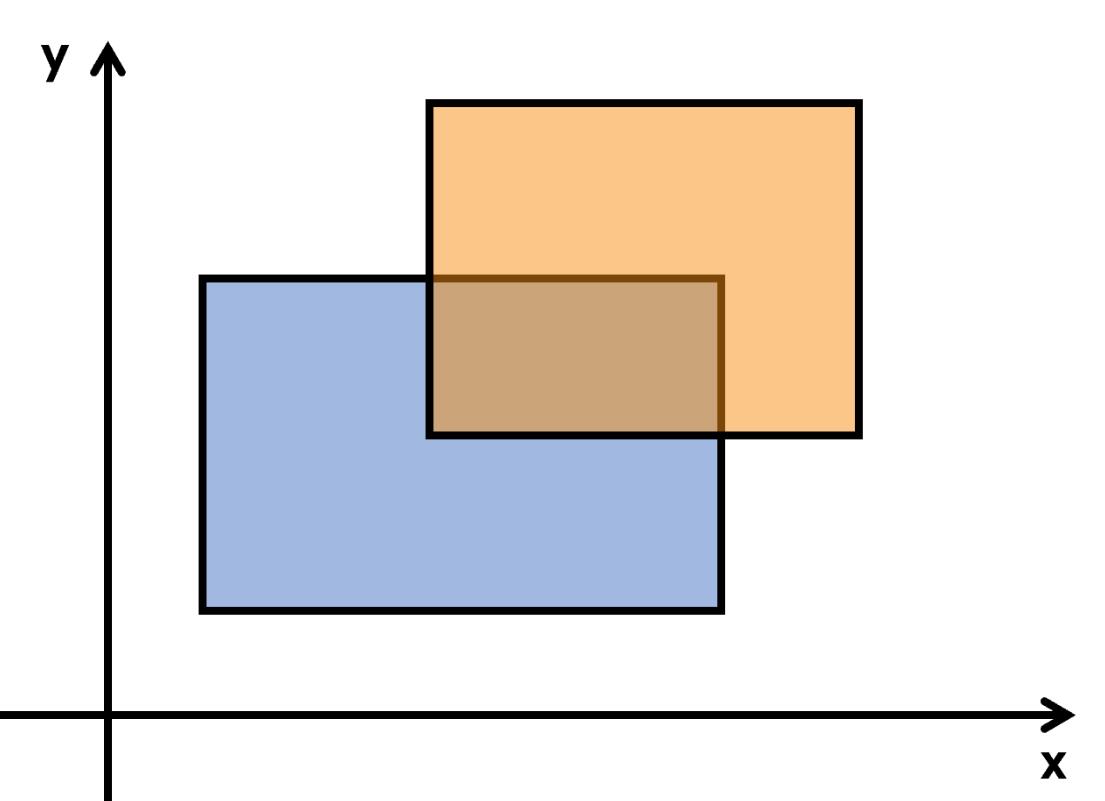
- 对于当前的截线段长度, 为了快速计算出截线段长度, 我们可以将矩形的横边附上不同的长度(下边权1,上边权-1),因为已经按高度从下到上排序,所以每次肯定会先遇到下边,再遇到上边,边权恒为正。 此时只要开一个数组维护横坐标信息,每次遇到一条边就将这条边对应的区间累加上边权1或-1的值,然后查询当前>1的区间长度,乘以高就是当前的面积。
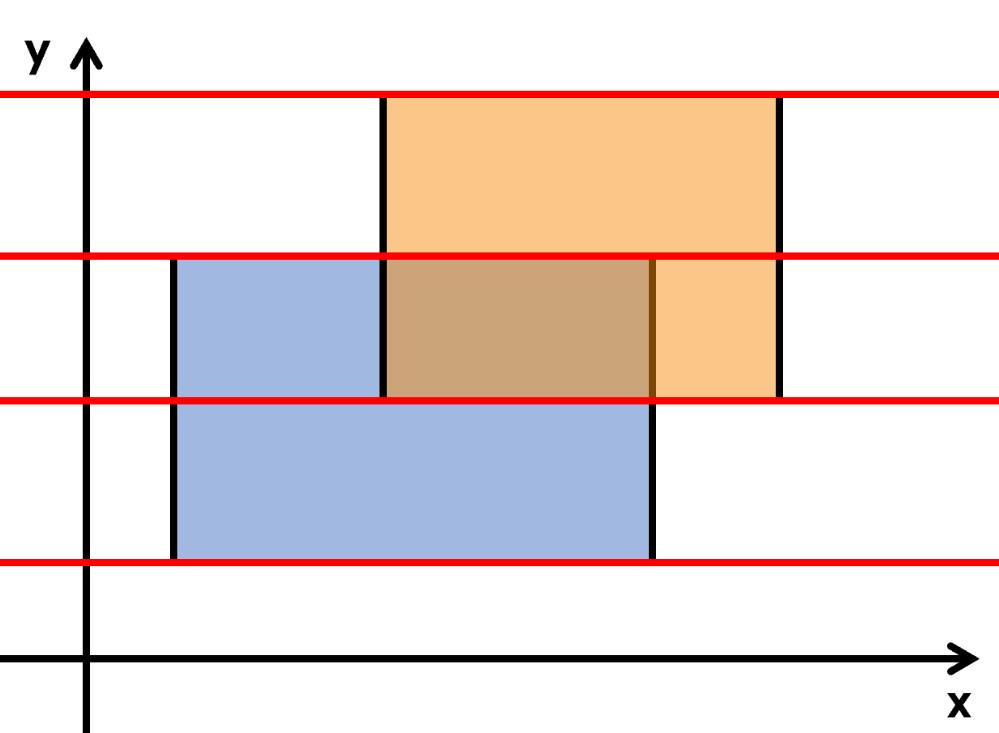
- 考虑用线段树优化区间查询和修改:为了和线段树扯上关系,先把所有端点在x轴上的端点离散化(存到映射数组X里排个序再去重,此时区间[1,n]与原先的区间[l,r]对应,查询通过X数组来实现)。 之后用线段树维护区间信息(当前线段被多少个矩形所覆盖sum, 该线段内被整个图形所截的长度len,扫描的时候给
[l,r]+=(1/-1)来更新,查询时直接查询根节点维护的长度)。 一个注意的要点是(建立X和线段树对应关系时,考虑对于线段树的一个叶节点x, 建树时保证tree[x].l=tree[x].r,但其保存的信息很显然不可能只是某条线段的一个端点,该区间对应到( X[tree[x].l] ,X[tree[x].r] )后,区间左右端点相减就没有意义了,所以考虑改变映射关系,让tree[x].{l,r} 对应到 X[ {l, r+1} ],即( X[tree[x].l],X[tree[x].r+1] )此时就可以运行了。
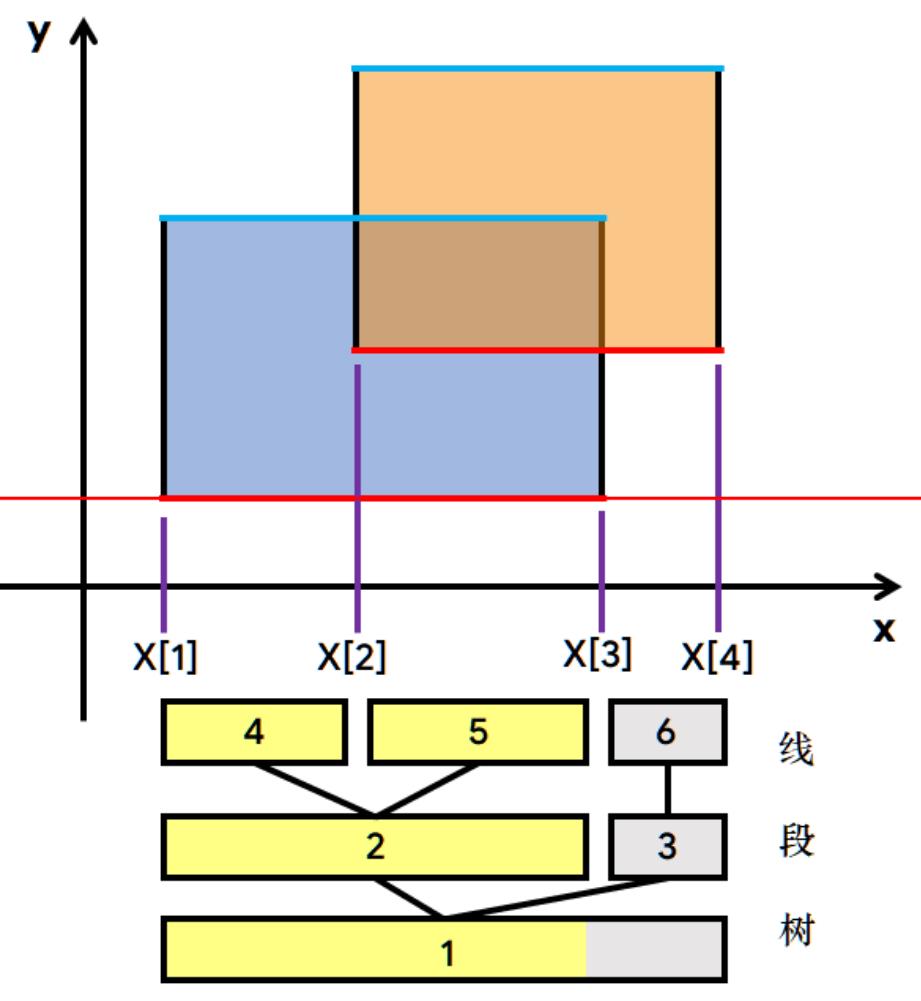
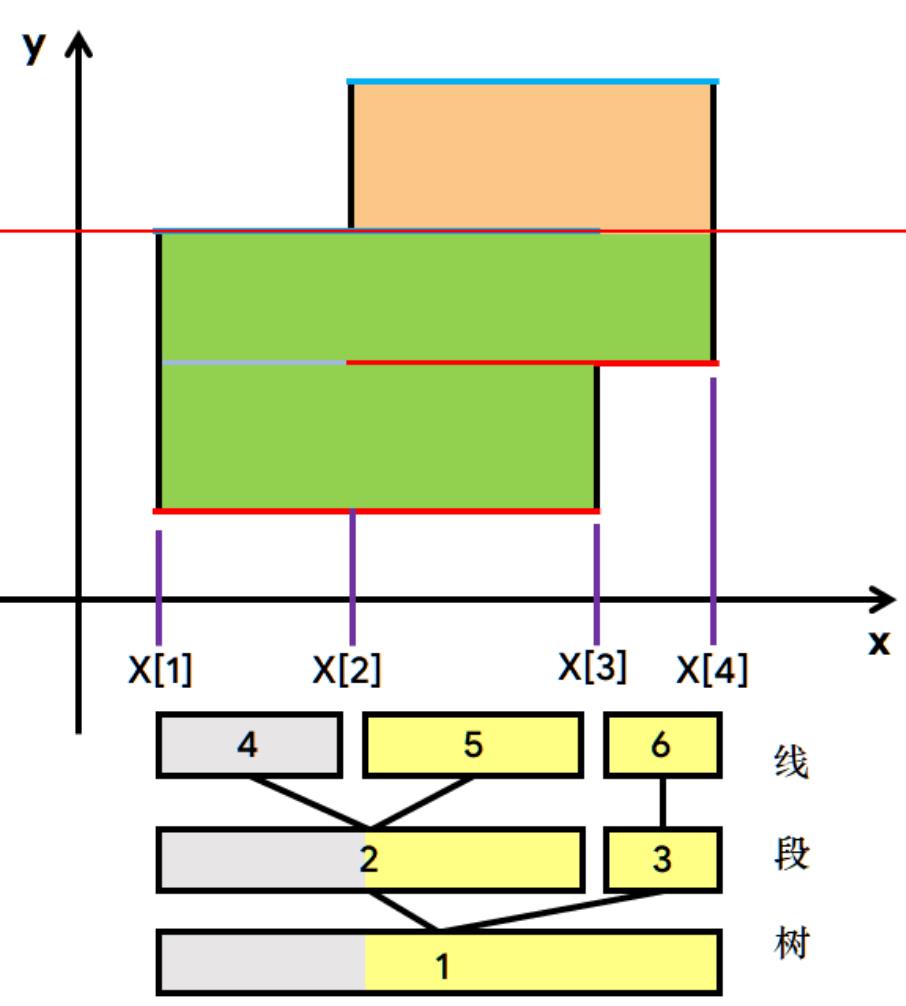
- 对于扫过的高度只需要将直线存起来按照高度h从下到上排序,每次的 (line[i+1].h-line[i].h) 就是扫过的高度。
//luogu5490 扫描线求矩形面积并
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int maxn = 1e6+10;
//扫描线: 维护线段端点X和线段信息line[l,r,h,(1/-1)]
LL X[maxn<<1];
struct Scan{ LL l, r, h; int mark; }line[maxn<<1];
bool operator < (Scan a,Scan b){return a.h<b.h;}
//线段树: sum维护被覆盖次数, len维护区间被截长度
#define lch (p<<1)
#define rch (p<<1|1)
struct Sgt{ int l, r, sum; LL len; }tree[maxn<<2];
void build(int p, int l, int r){
tree[p] = Sgt{l,r,0,0};
if(l==r)return ;
int mid = l+r>>1;
build(lch, l, mid);
build(rch, mid+1, r);
return ;
}
void push_up(int p){
int l = tree[p].l, r = tree[p].r;
if(tree[p].sum!=0){ //被覆盖
tree[p].len = X[r+1]-X[l];//更新长度,将线段树节点x的[l,r]与实际区间[X[l],X[r+1]]对应,保证了叶节点不是一个端点
}else{
tree[p].len = tree[lch].len+tree[rch].len;//合并儿子信息
}
}
void update(int p, LL L, LL R, int c){
int l = tree[p].l, r = tree[p].r;
if(X[r+1]<=L || R<=X[l])return ;
//考虑[2,5],[5,8]两条线段, 要修改[1,5]区间的sum
//虽然5在这个区间内,[5,8] 却并不是我们希望修改的线段
if(L <= X[l] && X[r+1]<=R){
tree[p].sum += c;
push_up(p);
return ;
}
update(lch,L,R,c);
update(rch,L,R,c);
push_up(p);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
LL n; cin>>n;
for(int i = 1; i <= n; i++){
LL x1, y1, x2, y2;
cin>>x1>>y1>>x2>>y2;
X[2*i-1]=x1, X[2*i]=x2;
line[2*i-1] = Scan{x1,x2,y1,1};
line[2*i] = Scan{x1,x2,y2,-1};
}
n <<= 1; //一共有2*n条线段
sort(line+1, line+n+1);
sort(X+1, X+n+1); //端点排序
int tot = unique(X+1,X+n+1)-X-1; //端点去重离散化,建立端点[l,r]与[1,n]的对应关系
build(1,1,tot-1); //用线段端点[X[1], X[tot]]建线段树
LL ans = 0;
for(int i = 1; i < n; i++){//最后一条边不用
update(1,line[i].l,line[i].r, line[i].mark);//扫描信息
ans += tree[1].len*(line[i+1].h-line[i].h);//统计面积
}
cout<<ans<<"\\n";
return 0;
}
//POJ1151 扫描线求矩形面积并
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
typedef long long LL;
using namespace std;
const int maxn = 500;
//扫描线: 维护线段端点X和线段信息line[l,r,h,(1/-1)]
double X[maxn<<1];
struct Scan{ double l, r, h; int mark; }line[maxn<<1];
bool operator < (Scan a,Scan b){return a.h<b.h;}
//线段树: sum维护被覆盖次数, len维护区间被截长度
#define lch (p<<1)
#define rch (p<<1|1)
struct Sgt{ int l, r, sum; double len; }tree[maxn<<2];
void build(int p, int l, int r){
tree[p] = Sgt{l,r,0,0};
if(l==r)return ;
int mid = l+r>>1;
build(lch, l, mid);
build(rch, mid+1, r);
return ;
}
void push_up(int p){
int l = tree[p].l, r = tree[p].r;
if(tree[p].sum!=0){
tree[p].len = X[r+1]-X[l];
}else{
tree[p].len = tree[lch].len+tree[rch].len;
}
}
void update(int p, double L, double R, int c){
int l = tree[p].l, r = tree[p].r;
if(X[r+1]<=L || R<=X[l])return ;
if(L <= X[l] && X[r+1]<=R){
tree[p].sum += c;
push_up(p);
return ;
}
update(lch,L,R,c);
update(rch,L,R,c);
push_up(p);
}
int main(){
LL n, k=0;
while(cin>>n &&n){
for(int i = 1; i <= n; i++){
double x1, y1, x2, y2;
cin>>x1>>y1>>x2>>y2;
X[2*i-1]=x1, X[2*i]=x2;
line[2*i-1] = Scan{x1,x2,y1,1};
line[2*i] = Scan{x1,x2,y2,-1};
}
n <<= 1;
sort(line+1, line+n+1);
sort(X+1, X+n+1);
int tot = unique(X+1,X+n+1)-X-1;
build(1,1,tot-1);
double ans = 0;
for(int i = 1; i < n; i++){
update(1,line[i].l,line[i].r, line[i].mark);
ans += tree[1].len*(line[i+1].h-line[i].h);
}
printf("Test case #%d\\n",++k);
printf("Total explored area: %.2f\\n\\n", ans);
memset(tree,0,sizeof(tree));
memset(X,0,sizeof(X));
memset(line,0,sizeof(line));
}
return 0;
}
以上是关于luogu5490POJ1151模板扫描线 /Atlantis (求矩形面积并)的主要内容,如果未能解决你的问题,请参考以下文章