小Y学算法⚡️每日LeetCode打卡⚡️——5.最长回文子串

Posted 2021-09-01 呆呆敲代码的小Y

• • • • 📢前言
  • 🌲原题样例
  • • • • 回文串含义
      • 🌻C#方法一：暴力法
      • 🌻C#方法二：中心扩展法
      • 🌻Java方法一：动态规划
      • 🌻Java方法一：中心扩展算法
  • 💬总结

---

📢前言

• 🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻
• 🌲 每天打卡一道算法题，既是一个学习过程，又是一个分享的过程😜
• 🌲 提示：本专栏解题 编程语言一律使用 C# 和 Java 两种进行解题
• 🌲 要保持一个每天都在学习的状态，让我们一起努力成为算法大神吧🧐！
• 🌲 今天是力扣算法题持续打卡第5天🎈！
• 🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻

---

🌲原题样例

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

示例 2：

输入：s = “cbbd”
输出：“bb”

示例 3：

输入：s = “a”
输出：“a”

示例 4：

输入：s = “ac”
输出：“a”

提示：

• 1 <= s.length <= 1000
• s 仅由数字和英文字母（大写和/或小写）组成

回文串含义

这里简单解释一下什么是回文串~

"回文串”就是一个正读和反读都一样的字符串，比如“mom”或者“noon”等等就是回文串。

顾名思义，“回文子串”的意思是一个字符串中的回文串，比如字符串“baba”中就包含有“bab”和“aba”这两个回文子串

---

🌻C#方法一：暴力法

解题思路

首先我们会想到使用 暴力法 来解决题目，用3层循环来对每个子串进行检查，最后取最长的子串作为结果，这样时间复杂度为 O(n^3) 。
然后可能会考虑到使用动态规划的方式，以空间来换取时间,可以将时间复杂度优化为 O(n^2)，但相应的空间复杂度会增大

public class Solution {
    public string LongestPalindrome(string s)
    {
        string result = "";
        int n = s.Length;
        for (int i = 0; i < n; i++)
        {
            for (int j = i; j < n; j++)
            {
                // 检查 s[i]到s[j]是否是回文串，如果是，且长度大于result长度，就更新它
                int p = i, q = j;
                bool isPalindromic = true;
                while (p < q)
                {
                    if (s[p++] != s[q--])
                    {
                        isPalindromic = false;
                        break;
                    }
                }
                if (isPalindromic)
                {
                    int len = j - i + 1;
                    if (len > result.Length)
                    {
                        result = s.Substring(i, len);
                    }
                }

            }
        }
        return result;
    }

}
链接：https://leetcode-cn.com/problems/longest-palindromic-substring/solution/leetcode-5-longest-palindromic-substring-zui-chang/

执行结果
执行结果 通过，执行用时 1708ms，内存消耗 26.5 MB

复杂度分析

时间复杂度： O(n^3)
空间复杂度：O(1)

🌻C#方法二：中心扩展法

对于回文串，我们可以找到一个中心，从这个中心向两边扩展的话，两边对应的值是相等的。按照这个逻辑，我们只需要一层主循环 i 将 s 遍历一遍即可,并在循环内部 将s[i]视为中心 使用中心扩展法来求出以s[i]为中心的最长的回文串；当i将s遍历完后，即可得到s的最长回文串。

下面我们以 s=“abcbc”, 且 i==2 为例，讨论一下如何进行中心扩展。

1. i==2指向c，我们初始化两个指针p与q都指向这个c
2. p–，q++，p指向了左边b，q指向了右边b
3. 因为s[p]==s[q], 所以再次执行p–,q++,此时p指向了最左边a，q指向了最右边c
4. 因为s[p]!=s[q],所以结束扩展。

此时，我们得到了当i指向中间c时的最长回文子串为"bcb",长度为 q-p-1,开始位置为p+1. 对应图解图下：

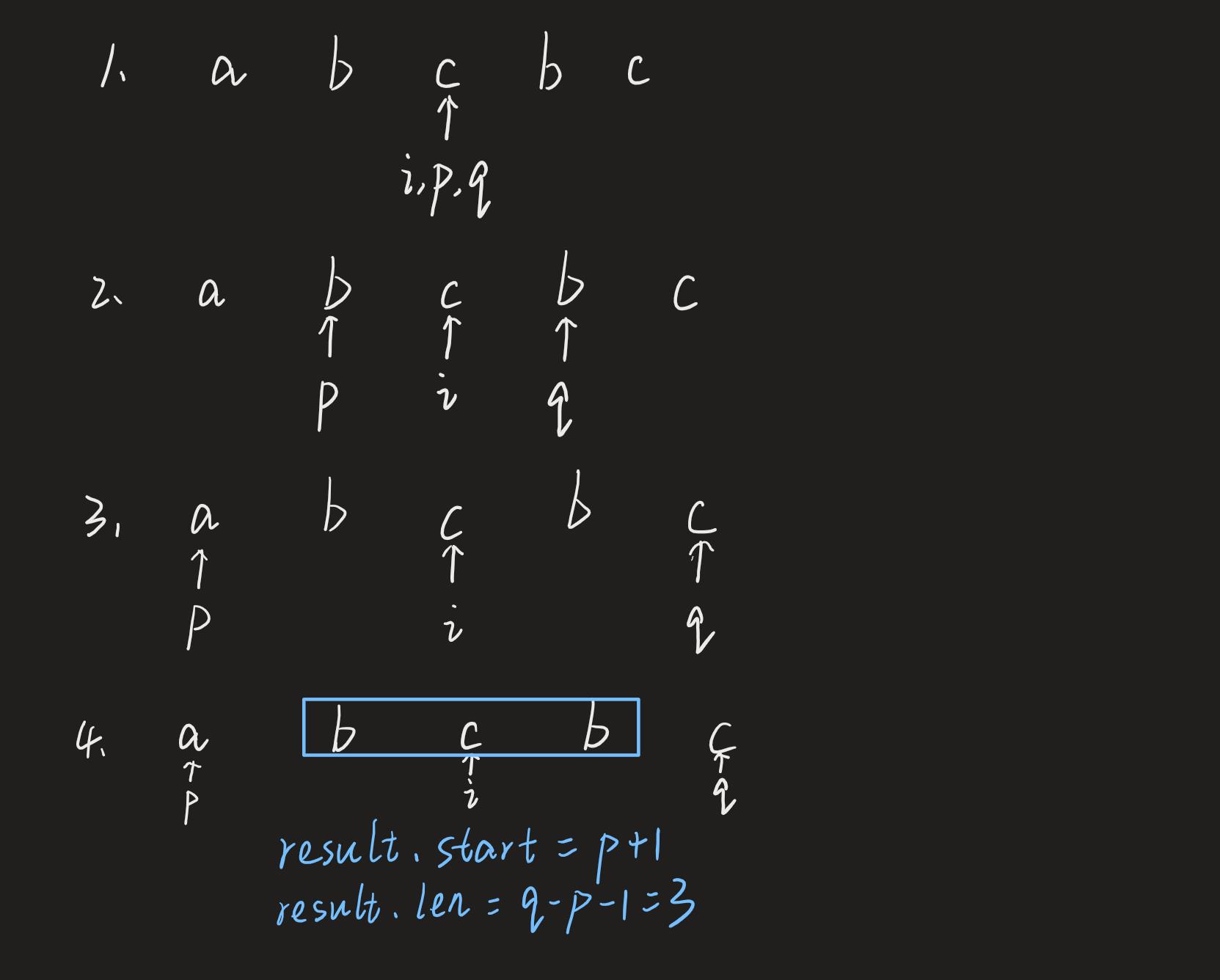
当子串长度为奇数时，这个逻辑很容易理解； 当子串长度为偶数时，比如 “abba”，我们需要把中心理解为中轴线，即中轴线在两个b的中间。

将中心理解为中轴线后，中轴线既可以在整数位上，例如"aba"中的b，也可以在两数之间，例如"abba"中的bb之间。若我们用mid表示中轴线，则mid可以等于0、1、2… 也可以等于0.5、1.5、2.5… 对于长度为n的数组，中轴线的选择有 n 个，i 的取值为0到 2(n-1) .。

代码为：

public class Solution {
    public string LongestPalindrome(string s)
    {
        string result = "";
        int n = s.Length;
        int end = 2 * n - 1;
        for (int i = 0; i < end; i ++)
        {
            double mid = i / 2.0;
            int p = (int)(Math.Floor(mid));
            int q = (int)(Math.Ceiling(mid));
            while (p >= 0 && q < n)
            {
                if (s[p] != s[q]) break;
                p--; q++;
            }
            int len = q - p - 1;
            if (len > result.Length)
                result = s.Substring(p + 1, len);
        }
        return result;
    }
}
链接：https://leetcode-cn.com/problems/longest-palindromic-substring/solution/leetcode-5-longest-palindromic-substring-zui-chang/

执行结果
执行结果 通过，执行用时88ms，内存消耗 26 MB

复杂度分析

时间复杂度： O(n^2)
空间复杂度：O(1)

---

🌻Java方法一：动态规划

Java方法也是力扣官方对此题的解答，可以参考答案

根据这个思路，我们就可以完成动态规划了，最终的答案即为所有 P(i, j) = \\text{true}P(i,j)=true 中 j-i+1j−i+1（即子串长度）的最大值。注意：在状态转移方程中，我们是从长度较短的字符串向长度较长的字符串进行转移的，因此一定要注意动态规划的循环顺序。

public class Solution {

    public String longestPalindrome(String s) {
        int len = s.length();
        if (len < 2) {
            return s;
        }

        int maxLen = 1;
        int begin = 0;
        // dp[i][j] 表示 s[i..j] 是否是回文串
        boolean[][] dp = new boolean[len][len];
        // 初始化：所有长度为 1 的子串都是回文串
        for (int i = 0; i < len; i++) {
            dp[i][i] = true;
        }

        char[] charArray = s.toCharArray();
        // 递推开始
        // 先枚举子串长度
        for (int L = 2; L <= len; L++) {
            // 枚举左边界，左边界的上限设置可以宽松一些
            for (int i = 0; i < len; i++) {
                // 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
                int j = L + i - 1;
                // 如果右边界越界，就可以退出当前循环
                if (j >= len) {
                    break;
                }

                if (charArray[i] != charArray[j]) {
                    dp[i][j] = false;
                } else {
                    if (j - i < 3) {
                        dp[i][j] = true;
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }

                // 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置
                if (dp[i][j] && j - i + 1 > maxLen) {
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }
        return s.substring(begin, begin + maxLen);
    }
}

执行结果
执行结果 通过，执行用时178ms，内存消耗 42.9 MB

复杂度分析

时间复杂度： O(n^2)
空间复杂度：O(n^2)

🌻Java方法一：中心扩展算法

思路与算法

可以发现，所有的状态在转移的时候的可能性都是唯一的。也就是说，我们可以从每一种边界情况开始「扩展」，也可以得出所有的状态对应的答案。

边界情况即为子串长度为 11 或 22 的情况。我们枚举每一种边界情况，并从对应的子串开始不断地向两边扩展。如果两边的字母相同，我们就可以继续扩展，例如从 P(i+1,j-1)P(i+1,j−1) 扩展到 P(i,j)P(i,j)；如果两边的字母不同，我们就可以停止扩展，因为在这之后的子串都不能是回文串了。

聪明的读者此时应该可以发现，「边界情况」对应的子串实际上就是我们「扩展」出的回文串的「回文中心」。方法二的本质即为：我们枚举所有的「回文中心」并尝试「扩展」，直到无法扩展为止，此时的回文串长度即为此「回文中心」下的最长回文串长度。我们对所有的长度求出最大值，即可得到最终的答案。

class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 1) {
            return "";
        }
        int start = 0, end = 0;
        for (int i = 0; i < s.length(); i++) {
            int len1 = expandAroundCenter(s, i, i);
            int len2 = expandAroundCenter(s, i, i + 1);
            int len = Math.max(len1, len2);
            if (len > end - start) {
                start = i - (len - 1) / 2;
                end = i + len / 2;
            }
        }
        return s.substring(start, end + 1);
    }

    public int expandAroundCenter(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            --left;
            ++right;
        }
        return right - left - 1;
    }
}

执行结果
执行结果 通过，执行用时38ms，内存消耗 30.8 MB

复杂度分析

时间复杂度： O(n^2)
空间复杂度：O(1)

---

💬总结

• 今天是力扣算法题打卡的第五天！今天的题有点难，借助力扣大神题解看了半天！
• 文章采用 C# 和 Java 两种编程语言进行解题
• 一些方法也是参考力扣大神写的，也是边学习边分享，再次感谢算法大佬们
• 那今天的算法题分享到此结束啦，明天再见！