MATLAB点云处理（二十一）：点云旋转平移（详细解读！）
Posted 没事就要敲代码
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了MATLAB点云处理（二十一）：点云旋转平移（详细解读！）相关的知识，希望对你有一定的参考价值。
1 刚体运动变换基础知识
刚体运动变换，即刚性变换，是指在三维空间中，把一个物体做旋转、平移，是一种保持物体大小和形状不变的仿射变换，刚体变换又称为欧式变换、齐次变换。
1.1 旋转矩阵
用3×3的旋转矩阵（Rotation Matrix）来描述刚体运动变换中的旋转变换。通常我们说的旋转矩阵均为正方向旋转。
那么旋转方向的正负（逆）是怎样界定的呢？
满足右手准则： 伸出右手，大拇指指向坐标轴正方向，四指握住坐标轴，四指弯曲的方向即为该轴的旋转的正方向。
若未特殊说明，以下旋转均为在右手坐标系下的正旋转。
以绕Z轴旋转为例：
坐标转换公式如下：
{
x
′
=
x
c
o
s
β
−
y
s
i
n
β
y
′
=
x
s
i
n
β
+
y
c
o
s
β
z
′
=
z
\\begin{cases} x'=xcos\\beta-ysin\\beta\\\\ y'=xsin\\beta+ycos\\beta\\\\ z'=z\\\\ \\end{cases}
⎩⎪⎨⎪⎧x′=xcosβ−ysinβy′=xsinβ+ycosβz′=z
旋转矩阵为：
[
c
o
s
β
−
s
i
n
β
0
s
i
n
β
c
o
s
β
0
0
0
1
]
\\begin{bmatrix} cos\\beta&-sin\\beta&0\\\\ sin\\beta&cos\\beta&0\\\\ 0&0&1\\\\ \\end{bmatrix}
⎣⎡cosβsinβ0−sinβcosβ0001⎦⎤
同理，绕X轴旋转的公式为：
{
x
′
=
x
y
′
=
y
c
o
s
β
−
z
s
i
n
β
z
′
=
y
s
i
n
β
+
z
c
o
s
β
\\begin{cases} x'=x\\\\ y'=ycos\\beta-zsin\\beta\\\\ z'=ysin\\beta+zcos\\beta\\\\ \\end{cases}
⎩⎪⎨⎪⎧x′=xy′=ycosβ−zsinβz′=ysinβ+zcosβ
旋转矩阵为：
[
1
0
0
0
c
o
s
β
−
s
i
n
β
0
s
i
n
β
c
o
s
β
]
\\begin{bmatrix} 1&0&0\\\\ 0&cos\\beta&-sin\\beta\\\\ 0&sin\\beta&cos\\beta\\\\ \\end{bmatrix}
⎣⎡1000cosβsinβ0−sinβcosβ⎦⎤
绕Y轴旋转的公式为：
{
x
′
=
x
c
o
s
β
+
z
s
i
n
β
y
′
=
y
z
′
=
−
x
s
i
n
β
+
z
c
o
s
β
\\begin{cases} x'=xcos\\beta+zsin\\beta\\\\ y'=y\\\\ z'=-xsin\\beta+zcos\\beta\\\\ \\end{cases}
⎩⎪⎨⎪⎧x′=xcosβ+zsinβy′=yz′=−xsinβ+zcosβ
旋转矩阵为：
[
c
o
s
β
0
s
i
n
β
0
1
0
−
s
i
n
β
0
c
o
s
β
]
\\begin{bmatrix} cos\\beta&0&sin\\beta\\\\ 0&1&0\\\\ -sin\\beta&0&cos\\beta\\\\ \\end{bmatrix}
⎣⎡cosβ0−sinβ010sinβ0cosβ⎦⎤
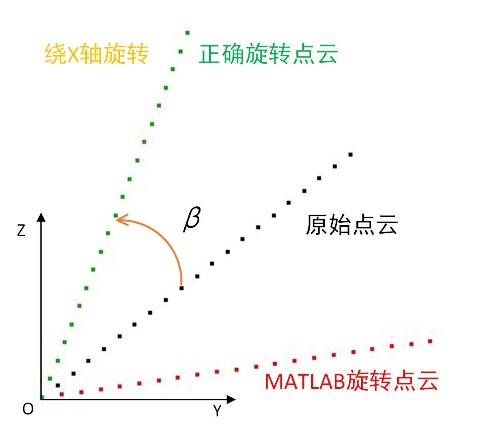
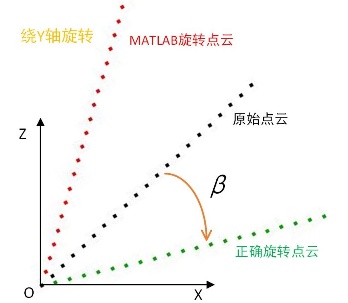
特别注意的是！！！
MATLAB 中的旋转矩阵与实际的旋转矩阵 相差一个负号 ，因此MATLAB应用与以上旋转矩阵时，均为 逆旋转。
绕Z轴旋转
绕X轴旋转
绕Y轴旋转
1.2 平移向量
点云平移较为简单，平移参数为1×3的行向量，分别表示3个轴向的平移量
[
t
x
,
t
y
,
t
z
]
[t_x,t_y,t_z]
[tx,ty,tz]
1.3 坐标转换矩阵（旋转+平移）
绕X轴旋转：
[
1
0
0
0
0
c
o
s
β
−
s
i
n
β
0
0
s
i
n
β
c
o
s
β
0
t
x
t
y
t
z
1
]
\\begin{bmatrix} 1&0&0&0\\\\ 0&cos\\beta&-sin\\beta&0\\\\ 0&sin\\beta&cos\\beta&0\\\\ t_x&t_y&t_z&1\\\\ \\end{bmatrix}
⎣⎢⎢⎡100tx0cosβsinβty0−sinβcosβtz0001⎦⎥⎥⎤
绕Y轴旋转：
[
c
o
s
β
0
s
i
n
β
0
0
1
0
0
−
s
i
n
β
0
c
o
s
β
0
t
x
t
y
t
z
1
]
\\begin{bmatrix} cos\\beta&0&sin\\beta&0\\\\ 0&1&0&0\\\\ -sin\\beta&0&cos\\beta&0\\\\ t_x&t_y&t_z&1\\\\ \\end{bmatrix}
⎣⎢⎢⎡cosβ0−sinβMATLAB点云处理（二十）：三维刚体几何变换矩阵（regid3d）与仿射几何变换矩阵（affine3d）
MATLAB点云处理（二十三）：读写LAS点云（lasFileReader | lasFileWriter）
MATLAB点云处理（二十六）：将无序点云转换为有序点云（pcorganize），删除无效点（removeInvalidPoints）
MATLAB点云处理（二十六）：将无序点云转换为有序点云（pcorganize），删除无效点（removeInvalidPoints）