FIR滤波器设计之窗函数法
Posted Zhi Zhao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了FIR滤波器设计之窗函数法相关的知识,希望对你有一定的参考价值。
前言
FIR滤波器是指有限长冲激响应滤波器。它可以设计成严格线性相位,能避免被处理的信号产生相位失真,因而在数据通信、语音信号处理、图像处理等领域应用广泛。
一、窗函数法的基本原理
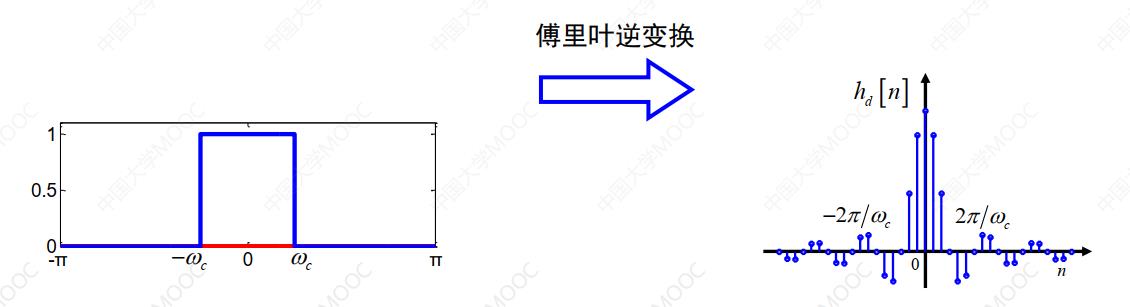
给定一个理想的零相位低通滤波器,其频率特性可表示为:

零相位滤波器的特点为:

对应的单位冲激响应为:

式(1)和式(2)分别对应图1中的频域和时域,上述过程即做了傅里叶逆变换。
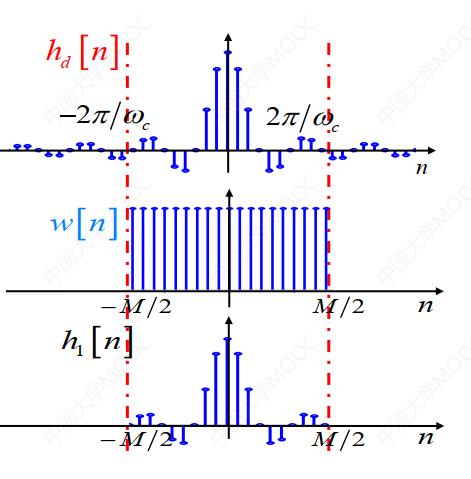
由于 是一个无限长序列,计算机通常是无法处理的,因此用一个函数w(n)对其进行截断,变成一个有限长序列h(n),即:
是一个无限长序列,计算机通常是无法处理的,因此用一个函数w(n)对其进行截断,变成一个有限长序列h(n),即:

w(n)称为窗函数,其表达式如下:

无限长序列截取为有限长序列的过程如图2所示。
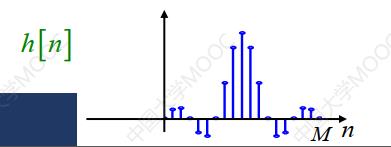
由于此时的h(n)是非因果序列,是不可实现的,对其在时域上进行移位,得到新的h(n)如下式:

式(5)为可实现的低通滤波器的时域表达式,其波形图如图3所示。
另外,也可以对 先做时域上的移位,再利用窗函数进行截取,并且截取过程中序列保持为对称的。此时的序列h(n)为有限长因果序列。
先做时域上的移位,再利用窗函数进行截取,并且截取过程中序列保持为对称的。此时的序列h(n)为有限长因果序列。
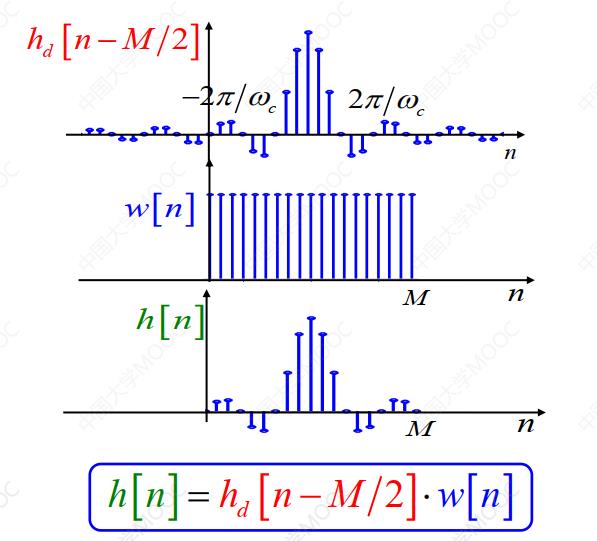
根据时域移位性质:幅频不变,相频线性变化。


窗函数w(n)的频域表达式为:

根据时域相乘等于频域卷积,可实现的滤波器的频域表达式为:

具有理想线性相位的 与窗函数w(n)的频谱如图5所示。
与窗函数w(n)的频谱如图5所示。
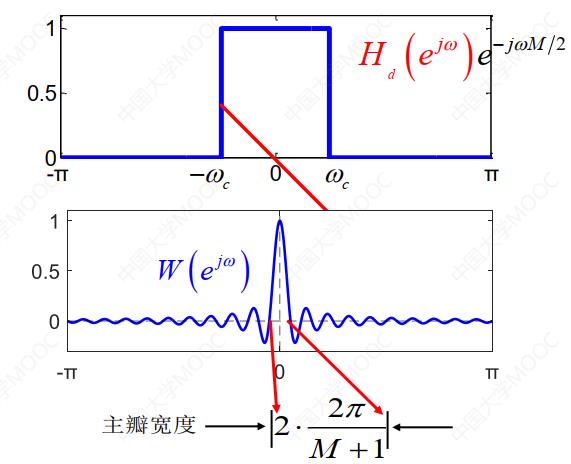
主瓣宽度为4π/N,N为窗函数的长度,N=M+1,M为滤波器的阶数。
最终得到的可实现的滤波器为理想滤波器 与窗函数w(n)的卷积,如图6所示。
与窗函数w(n)的卷积,如图6所示。
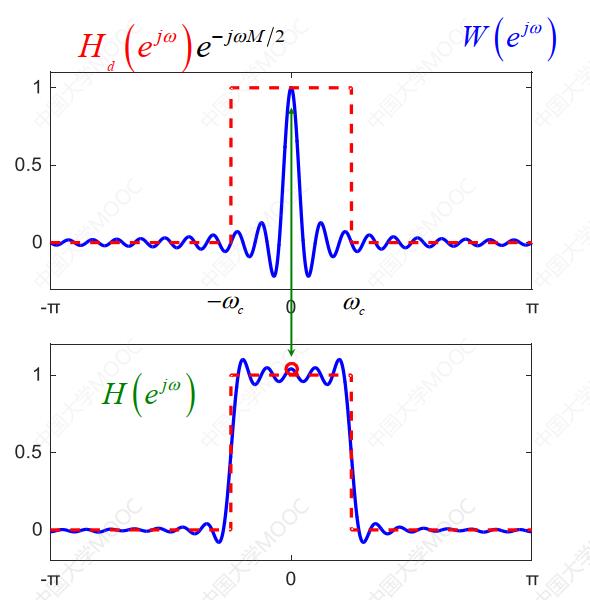
窗函数法设计的滤波器有如下结论:
1)旁瓣积分决定阻带和通带内的纹波;
2)主瓣积分决定过渡带的宽度。
3)通带的幅度取决于主、旁瓣积分。
二、窗函数法设计步骤
由于窗的形状影响主瓣和旁瓣,所以设计滤波器时根据纹波大小确定窗的形状;窗的长度影响主瓣,进而影响过渡带宽度,所以设计滤波器时根据过渡带宽度确定窗的长度。
设计一个FIR滤波器通常按照下面的步骤进行:
1)根据滤波器设计要求指标,确定滤波器的阻带衰减要求和过渡带宽度,进而选择窗函数的类型并估计窗的长度N;
2)根据过渡带宽度确定理想滤波器的截止频率,得到单位脉冲响应 ;
;
3)根据求得的可实现滤波器h(n)的表达式,求出其频率响应:

4)根据频率响应验证是否满足技术指标;
5)若不满足指标要求,则应调整窗函数类型或长度,然后重复以上步骤,直到满足要求为止。
三、案例分析



四、MATLAB代码
function [h] = useFIR(mode,n,fp,fs,window,r,sample)
% mode:模式(1——高通,2——低通,3——带通,4——带阻)
% n:阶数,加窗的点数为阶数加1
% fp:高通和低通时指示截止频率,带通和带阻时指示下限频率
% fs:带通和带阻时指示上限频率
% window:加窗(1——矩形窗,2——三角窗,3——巴特窗,4——海明窗,
% 5——汉宁窗,6——布莱克曼窗,7——凯塞窗,8——切比雪夫窗)
% r:代表加kaiser窗时的beta值和加chebyshev窗的r值
% sample:采样率
% h:返回设计好的FIR滤波器系数
if window == 1
w = boxcar(n+1);
end
if window == 2
w = triang(n+1);
end
if window == 3
w = bartlett(n+1);
end
if window == 4
w = hamming(n+1);
end
if window == 5
w = hanning(n+1);
end
if window == 6
w = blackman(n+1);
end
if window == 7
w = kaiser(n+1,r);
end
if window == 8
w = chebwin(n+1,r);
end
wp = 2*fp/sample;
ws = 2*fs/sample;
if mode == 1
h = fir1(n,wp,'high',w);
end
if mode == 2
h = fir1(n,wp,'low',w);
end
if mode == 3
h = fir1(n,[wp,ws],w);
end
if mode == 4
h = fir1(n,[wp,ws],'stop',w);
end
m = 0:n;
subplot(1,3,1);plot(m,h);
xlabel('n');ylabel('h(n)');title('冲激响应');axis([0 n 1.1*min(h) 1.1*max(h)]);grid on;
freq_response = freqz(h,1);
magnitude = 20*log10(abs(freq_response));
m = 0:511;
f = m * sample/(2*511);
subplot(1,3,2);plot(f,magnitude);
xlabel('频率/Hz');ylabel('f幅值');title('幅频特性');axis([0 sample/2 1.1*min(magnitude) 1.1*max(magnitude)]);grid on;
phase = angle(freq_response);
subplot(1,3,3);plot(f,phase);
xlabel('频率/Hz');ylabel('相位');title('相频特性');axis([0 sample/2 1.1*min(phase) 1.1*max(phase)]);grid on;
end以上是关于FIR滤波器设计之窗函数法的主要内容,如果未能解决你的问题,请参考以下文章