fasttext的原理剖析
Posted ZSYL
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了fasttext的原理剖析相关的知识,希望对你有一定的参考价值。
fastText的原理剖析
1. fastText的模型架构
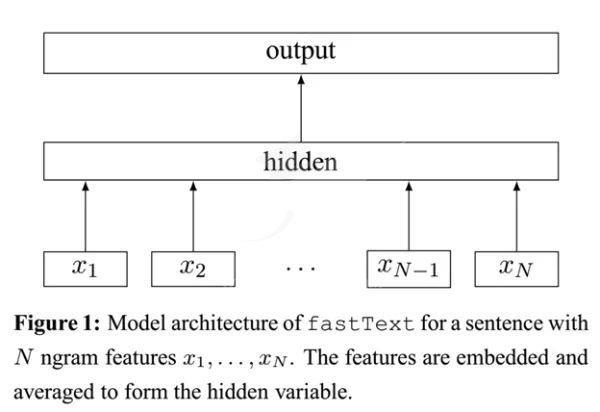
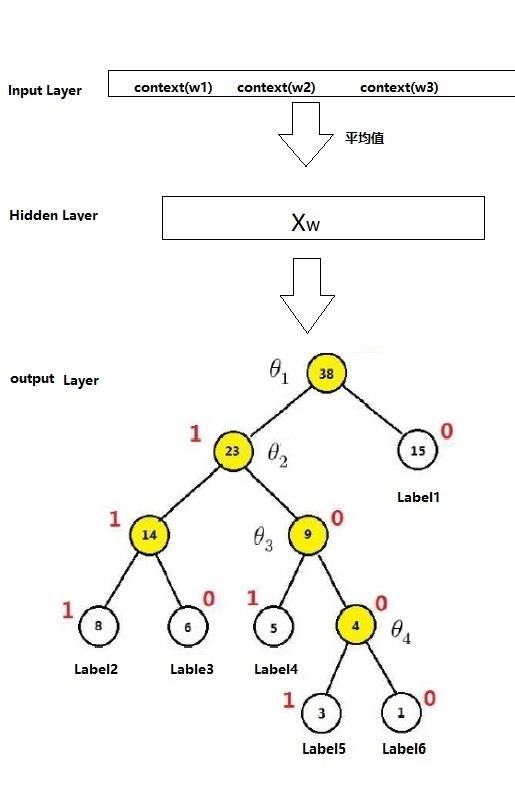
fastText的架构非常简单,有三层:输入层、隐含层、输出层(Hierarchical Softmax)
输入层:是对文档embedding之后的向量,包含有N-garm特征
隐藏层:是对输入数据的求和平均
输出层:是文档对应标签
如下图所示:
1.1 N-garm的理解
1.1.1 bag of word
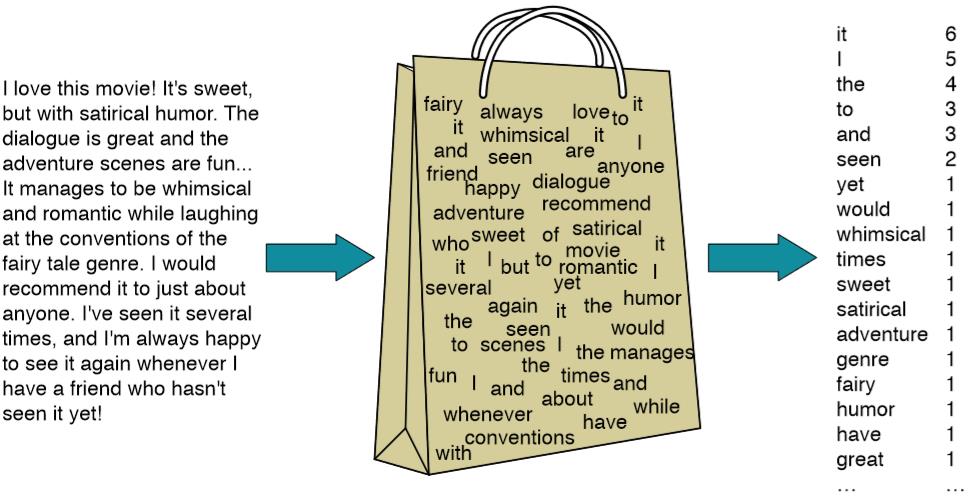
bag of word 又称为bow,称为词袋。是一种只统计词频的手段。
例如:在机器学习的课程中通过朴素贝叶斯来预测文本的类别,我们学习的countVectorizer和TfidfVectorizer都可以理解为一种bow模型。
1.1.2 N-gram模型
但是在很多情况下,词袋模型是不满足我们的需求的。
例如:我爱她 和她爱我在词袋模型下面,概率完全相同,但是其含义确实差别非常大。
为了解决这个问题,就有了N-gram模型,它不仅考虑词频,还会考虑当前词前面的词语,比如我爱,她爱。
N-gram模型的描述是:第n个词出现与前n-1个词相关,而与其他任何词不相关。(当然在很多场景下和前n-1个词也会相关,但是为了简化问题,经常会这样去计算)
例如:I love deep learning这个句子,在n=2的情况下,可以表示为{i love},{love deep},{deep learning},n=3的情况下,可以表示为{I love deep},{love deep learning}。
在n=2的情况下,这个模型被称为Bi-garm(二元n-garm模型)
在n=3 的情况下,这个模型被称为Tri-garm(三元n-garm模型)
具体可以参考 ed3book chapter3
所以在fasttext的输入层,不仅有分词之后的词语,还有包含有N-gram的组合词语一起作为输入
2. fastText中的层次化的softmax-对传统softmax的优化方法1
为了提高效率,在fastText中计算分类标签的概率的时候,不再是使用传统的softmax来进行多分类的计算,而是使用的哈夫曼树(Huffman,也成为霍夫曼树),使用层次化的softmax(Hierarchial softmax)来进行概率的计算。
2.1 哈夫曼树
2.1.1 哈夫曼树的定义
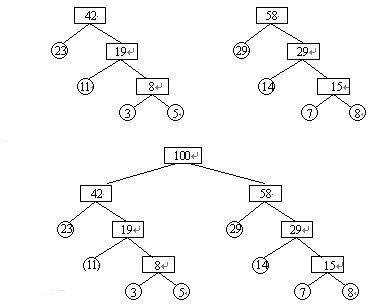
哈夫曼树概念:给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
2.1.2 哈夫曼树的相关概念
二叉树:每个节点最多有2个子树的有序树,两个子树分别称为左子树、右子树。有序的意思是:树有左右之分,不能颠倒
叶子节点:一棵树当中没有子结点的结点称为叶子结点,简称“叶子”
路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和
树的高度:树中结点的最大层次。包含n个结点的二叉树的高度至少为log2 (n+1)。
2.1.3 哈夫曼树的构造算法
- 把 { W 1 , W 2 , W 3 … W n } \\{W_1,W_2,W_3 \\dots W_n\\} {W1,W2,W3…Wn}看成n棵树的森林
- 在森林中选择两个根节点权值最小的树进行合并,作为一颗新树的左右子树,新树的根节点权值为左右子树的和
- 删除之前选择出的子树,把新树加入森林
- 重复2-3步骤,直到森林只有一棵树为止,概树就是所求的哈夫曼树
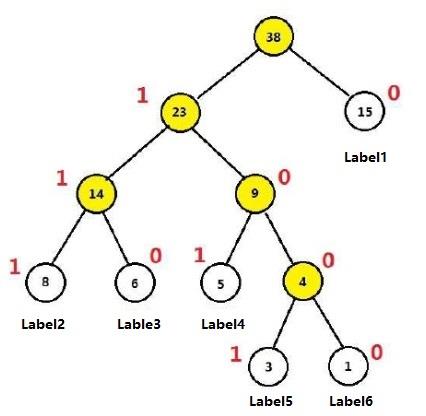
例如:圆圈中的表示每个词语出现的次数,以这些词语为叶子节点构造的哈夫曼树过程如下:
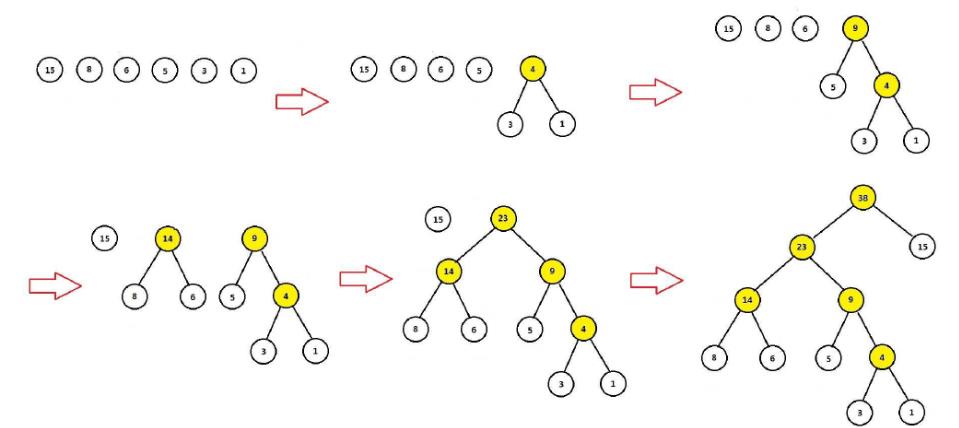
可见:
- 权重越大,距离根节点越近
- 叶子的个数为n,构造哈夫曼树中新增的节点的个数为n-1
2.2 哈夫曼编码
2.2.1 哈夫曼编码
在数据通信中,需要将传送的文字转换成二进制的字符串,用0,1码的不同排列来表示字符。
例如,需传送的报文为AFTER DATA EAR ARE ART AREA,这里用到的字符集为A,E,R,T,F,D,各字母出现的次数为{8,4,5,3,1,1}。现要求为这些字母设计编码。要区别6个字母,最简单的二进制编码方式是等长编码,固定采用3位二进制,可分别用000、001、010、011、100、101对A,E,R,T,F,D进行编码发送
但是很明显,上述的编码的方式并不是最优的,即整理传送的字节数量并不是最少的。
为了提高数据传送的效率,同时为了保证任一字符的编码都不是另一个字符编码的前缀,这种编码称为前缀编码[前缀编码],可以使用哈夫曼树生成哈夫曼编码解决问题
可用字符集中的每个字符作为叶子结点生成一棵编码二叉树,为了获得传送报文的最短长度,可将每个字符的出现频率作为字符结点的权值赋予该结点上,显然字使用频率越小权值越小,权值越小叶子就越靠下,于是频率小编码长,频率高编码短,这样就保证了此树的最小带权路径长度效果上就是传送报文的最短长度
因此,求传送报文的最短长度问题转化为求由字符集中的所有字符作为叶子结点,由字符出现频率作为其权值所产生的哈夫曼树的问题。利用哈夫曼树来设计二进制的前缀编码,既满足前缀编码的条件,又保证报文编码总长最短。
下图中label1 .... label6分别表示A,E,R,T,F,D
2.3 梯度计算
上图中,红色为哈夫曼编码,即label5的哈夫曼编码为1001,那么此时如何定义条件概率 P ( L a b e l 5 ∣ c o n t e x ) P(Label5|contex) P(Label5∣contex)呢?
以Label5为例,从根节点到Label5中间经历了4次分支,每次分支都可以认为是进行了一次2分类,根据哈夫曼编码,可以把路径中的每个非叶子节点0认为是负类,1认为是正类(也可以把0认为是正类)
由机器学习课程中逻辑回归使用sigmoid函数进行2分类的过程中,一个节点被分为正类的概率是 δ ( X T θ ) = 1 1 + e − X T θ \\delta(X^{T}\\theta) = \\frac{1}{1+e^{-X^T\\theta}} δ(XTθ)=1+e−XTθ1,被分类负类的概率是: 1 − δ ( X T θ ) 1-\\delta(X^T\\theta) 1−δ(XTθ),其中 θ \\theta θ就是图中非叶子节点对应的参数 θ \\theta θ。
对于从根节点出发,到达Label5一共经历4次2分类,将每次分类结果的概率写出来就是:
- 第一次: P ( 1 ∣ X , θ 1 ) = δ ( X T θ 1 ) P(1|X,\\theta_1) = \\delta(X^T\\theta_1) P(1∣X,θ1)=δ(XTθ1) ,即从根节点到23节点的概率是在知道X和 θ 1 \\theta_1 θ1的情况下取值为1的概率
- 第二次: P ( 0 ∣ X , θ 2 ) = 1 − δ ( X T θ 2 ) P(0|X,\\theta_2) =1- \\delta(X^T\\theta_2) P(0∣X,θ2)=1−δ(XTθ2)
- 第三次: P ( 0 ∣ X , θ 3 ) = 1 − δ ( X T θ 4 ) P(0 |X,\\theta_3) =1- \\delta(X^T\\theta_4) P(0∣X,θ3)=1−δ(XTθ4)
- 第四次: P ( 1 ∣ X , θ 4 ) = δ ( X T θ 4 ) P(1|X,\\theta_4) = \\delta(X^T\\theta_4) P(1∣X,θ4)=δ(XTθ4)
但是我们需要求的是
P
(
L
a
b
e
l
∣
c
o
n
t
e
x
)
P(Label|contex)
P(Label∣contex), 他等于前4词的概率的乘积,公式如下(
d
j
w
d_j^w
djw是第j个节点的哈夫曼编码)
P
(
L
a
b
e
l
∣
c
o
n
t
e
x
t
)
=
∏
j
=
2
5
P
(
d
j
∣
X
,
θ
j
−
1
)
P(Label|context) = \\prod_{j=2}^5P(d_j|X,\\theta_{j-1})
P(Label∣context)=j=2∏5P(dj∣X,θj−1)
其中:
P
(
d
j
∣
X
,
θ
j
−
1
)
=
{
δ
(
X
T
θ
j
−
1
)
,
d
j
=
1
;
1
−
δ
(
X
T
θ
j
−
1
)
d
j
=
0
;
P(d_j|X,\\theta_{j-1}) = \\left\\{ \\begin{aligned} &\\delta(X^T\\theta_{j-1}), & d_j=1;\\\\ &1-\\delta(X^T\\theta_{j-1}) & d_j=0; \\end{aligned} \\right.
P(dj∣X,θj−1)={δ(XTθj−1),1−δ(XTθj−1)dj=1;dj=0;
或者也可以写成一个整体,把目标值作为指数,之后取log之后会前置:
P
(
d
j
∣
X
,
θ
j
−
1
)
=
[
δ
(
X
T
θ
j
−
1
)
]
d
j
⋅
[
1
−
δ
(
X
T
θ
j
−
1
)
]
1
−
d
j
P(d_j|X,\\theta_{j-1}) = [\\delta(X^T\\theta_{j-1})]^{d_j} \\cdot [1-\\delta(X^T\\theta_{j-1})]^{1-d_j}
P(dj∣X,θj−1)=[δ(XTθj−1)]dj⋅[1−δ(X