排序4：堆排序HeapSort

Posted 2021-08-31 纵横千里，捭阖四方

堆结构就是将一颗完全二叉树映射到数组中的一种存储方式

heapInsert和heapify 大根堆最重要的两个操作就是heapInsert和heapify，前者是当一个元素加入到大根堆时应该自底向上与其父结点比较，若大于父结点则交换；后者是当堆中某个结点的数值发生变化时，应不断向下与其孩子结点中的最大值比较，若小于则交换。下面是对应的代码：

//判断该结点与父结点的大小，大结点一直往，建立大根堆
   public static void heapInsert(int[] arr,int index){
       while(arr[index]>arr[(index-1)/2]){
           swap(arr,index,(index-1)/2);
           index=(index-1)/2;
       }
   }    
   //一个值变小往下沉的过程
   public static void heapify(int[] arr,int index,int size){
       int left=index*2+1;
       while(left<size){
           int largest = left + 1 < size && arr[left+1] > arr[left] ? left+1 : left;
           largest = arr[largest] > arr[index] ? largest :index;
           if(largest==index){
               break;
           }
           swap(arr,largest,index);
           index=largest;
           left=index*2 +1;

       }
   }

 利用heapify排序：

 这个确实复杂一些：

public int[] MySort (int[] arr) {
       heapSort(arr);
       return arr;
   }

   public static void heapSort(int[] arr){
       if(arr == null || arr.length<2){
           return;
       }
       for(int i=0;i<arr.length;i++){
           heapInsert(arr,i); //构造完全二叉树
       }
       int size = arr.length;
       swap(arr,0,--size);
       while(size>0){
           heapify(arr,0,size);// 最后一个数与根交换
           swap(arr,0,--size);
       }

   }
   //判断该结点与父结点的大小，大结点一直往，建立大根堆
   public static void heapInsert(int[] arr,int index){
       while(arr[index]>arr[(index-1)/2]){
           swap(arr,index,(index-1)/2);
           index=(index-1)/2;
       }
   }

   //一个值变小往下沉的过程
   public static void heapify(int[] arr,int index,int size){
       int left=index*2+1;
       while(left<size){
           int largest = left + 1 < size && arr[left+1] > arr[left] ? left+1 : left;
           largest = arr[largest] > arr[index] ? largest :index;
           if(largest==index){
               break;
           }
           swap(arr,largest,index);
           index=largest;
           left=index*2 +1;

       }
   }

   //交换函数
   public static void swap(int[] arr, int i, int j){
       int tmp;
       tmp=arr[i];
       arr[i]=arr[j];
       arr[j]=tmp;
   }

2.优先级队列PriorityQueue

我们前一个专题专门分析了优先级队列的问题，这里再来看一下

优先队列不再遵循先入先出的原则，而是分为两种情况：

最大优先队列，无论入队顺序，当前最大的元素优先出队；

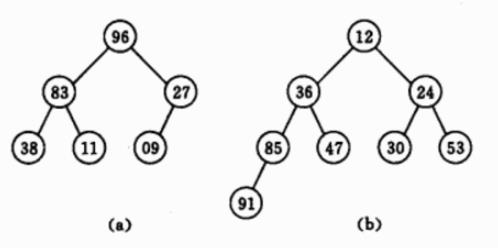
最小优先队列，无论入队顺序，当前最小的元素优先出队； 比如有一个最大优先队列，它的最大元素是8，那么虽然元素8并不是队首元素，但出队的时候仍然让元素8首先出队。 优先级队列，也叫二叉堆、堆（不要和内存中的堆区搞混了，一个是内存区域，一个是数据结构）。 ​堆的本质上是一种完全二叉树，分为： 小根堆：树中每个非叶子结点都不大于其左右孩子结点的值，也就是根节点最小的堆，图a 大根堆：树中每个非叶子结点都不小于其左右孩子结点的值，也就是根节点最大的堆，图b

  public int[] MySort (int[] arr) {
//         PriorityQueue<Integer> queue=new PriorityQueue<Integer>();
       PriorityQueue<Integer> queue=new PriorityQueue<>(new Comparator<Integer>(){
           public int compare(Integer a,Integer b){
               return a.compareTo(b);
           }
       });
       for(int i=0;i<arr.length;i++){
           queue.add(arr[i]);
       }
       int[] newarr=new int[arr.length];
       for(int i=0;i<arr.length;i++){
           newarr[i]=queue.poll();
       }
       return newarr;
   }