最短路算法（网络延迟时间）

Posted 2021-08-31 秦枫-_-

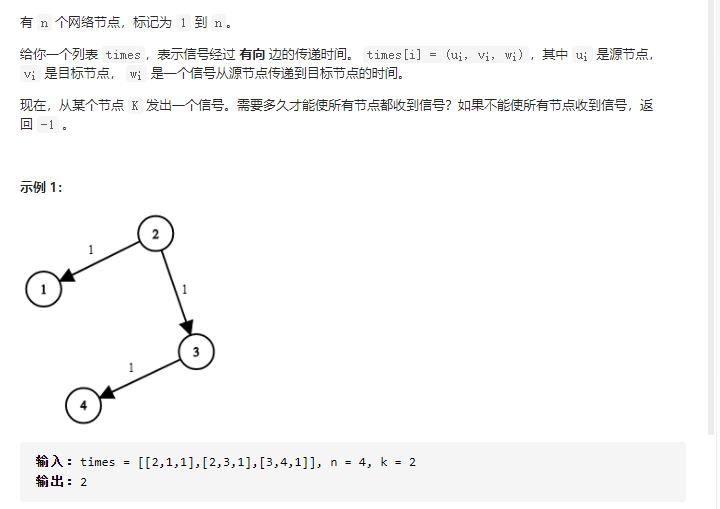
Dijkstra算法功能：给出加权连通图中一个顶点，称之为起点，找出起点到其它所有顶点之间的最短距离。


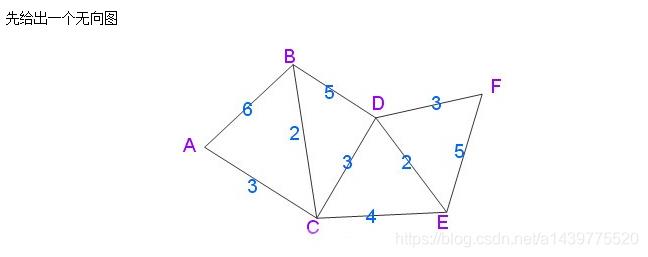
将所有节点分成两类：已确定从起点到当前点的最短路长度的节点，以及未确定从起点到当前点的最短路长度的节点（下面简称「未确定节点」和「已确定节点」）。

每次从「未确定节点」中取一个与起点距离最短的点，将它归类为「已确定节点」，并用它「更新」从起点到其他所有「未确定节点」的距离。直到所有点都被归类为「已确定节点」。

用节点 AA「更新」节点 BB 的意思是，用起点到节点 AA 的最短路长度加上从节点 AA 到节点 BB 的边的长度，去比较起点到节点 BB 的最短路长度，如果前者小于后者，就用前者更新后者。这种操作也被叫做「松弛」。

这里暗含的信息是：每次选择「未确定节点」时，起点到它的最短路径的长度可以被确定。

可以这样理解，因为我们已经用了每一个「已确定节点」更新过了当前节点，无需再次更新（因为一个点不能多次到达）。而当前节点已经是所有「未确定节点」中与起点距离最短的点，不可能被其它「未确定节点」更新。所以当前节点可以被归类为「已确定节点」。

class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
    int inf=Integer.MAX_VALUE/2;
    int [][]pic=new int[n][n];
    int []distance=new int[n];
    boolean []pass=new boolean[n];
    Arrays.fill(distance,inf);
    for(int i=0;i<n;i++){
        Arrays.fill(pic[i],inf);
    }
     for(int i=0;i<times.length;i++){
         pic[times[i][0]-1][times[i][1]-1]=times[i][2];
     }
     distance[k-1]=0;
     for(int i=0;i<n;i++){
         int idx=-1;
        for(int j=0;j<n;j++){
            if(!pass[j]&&(idx==-1||distance[j]<distance[idx]))
            idx=j;
        }
        pass[idx]=true;
        for(int j=0;j<n;j++){
            distance[j]=Math.min(distance[j],distance[idx]+pic[idx][j]);
        }
     }
     int ans=Arrays.stream(distance).max().getAsInt();
    return ans==inf?-1:ans;
    }
}