(计算机组成原理)第二章数据的表示和运算-第二节6:定点数除法运算(原码/补码一位除法)
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了(计算机组成原理)第二章数据的表示和运算-第二节6:定点数除法运算(原码/补码一位除法)相关的知识,希望对你有一定的参考价值。
一:除法运算基本思想
关于顶点数的除法,我们在小学其实就已经学习过了,就是列竖式除法,比如
0.211
÷
0.985
0.211÷0.985
0.211÷0.985,我们首先习惯同时扩大
n
n
n倍

在上面的例子中,
0.211
÷
0.985
=
0.214
0.211÷0.985=0.214
0.211÷0.985=0.214余210,它就等价于
0.211
=
0.985
×
0.214
+
0.000210
0.211=0.985×0.214+0.000210
0.211=0.985×0.214+0.000210,也就是说这可以转为成乘法的,也即
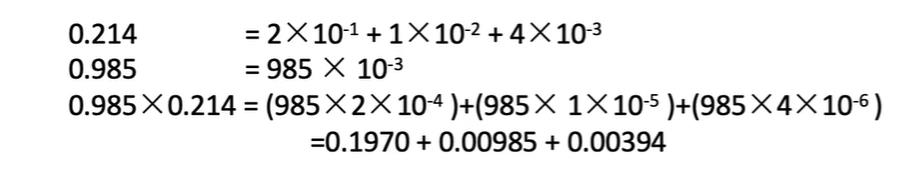
在计算机中,运算时使用的是二进制,比如
x
=
0.1011
x=0.1011
x=0.1011(被除数),
y
=
0.1101
y=0.1101
y=0.1101(除数),
x
÷
y
x÷y
x÷y如下
运算时忽略小数点,每确定一位商就进行一次减法,得到4位余数,在余数末尾补0,再确定下一位商,确定5位商即可停止(这里机器字长是5位)
- 如果补位后所得余数部分大于除数,那么就商1
- 如果补位后所得余数部分小于余数,那么就商0

和乘法一样,补全位数后就是下面这样

因此
x
÷
y
x÷y
x÷y结果为0.1101,余数为
0.00000111
0.00000111
0.00000111
二:原码一位除法:恢复余数法
(1)实现原理
逻辑看似很简单,但是如何让机器实现这是一个问题。其中符号位的处理就不用再强调了,和乘法一样,仍然使用异或完成,于是实际运算时采用两个数的绝对值完成。
c a s e : case : case:设机器字长为5位( n = 4 n=4 n=4,一位符号位), x = 0.1011 x=0.1011 x=0.1011, y = 0.1101 y=0.1101 y=0.1101,采用恢复余数法求 x ÷ y x÷y x÷y
- ∣ x ∣ = 0.1011 |x|=0.1011 ∣x∣=0.1011
- ∣ y ∣ = 0.1101 |y|=0.1101 ∣y∣=0.1101
- [ ∣ y ∣ ] 补 = 0.1101 [|y|]_{补}=0.1101 [∣y∣]补=0.1101
- [ − ∣ y ∣ ] 补 = 1.0011 [-|y|]_{补}=1.0011 [−∣y∣]补=1.0011
还记得(计算机组成原理)第一章计算机系统概述-第二节:计算机硬件组成(存储器、运算器和控制器概述及计算机工作过程详解)这一节我们讲到过的运算器的组成吗,其中涉及除法时会用到
A
C
C
ACC
ACC,
M
Q
MQ
MQ,
X
X
X这三个寄存器
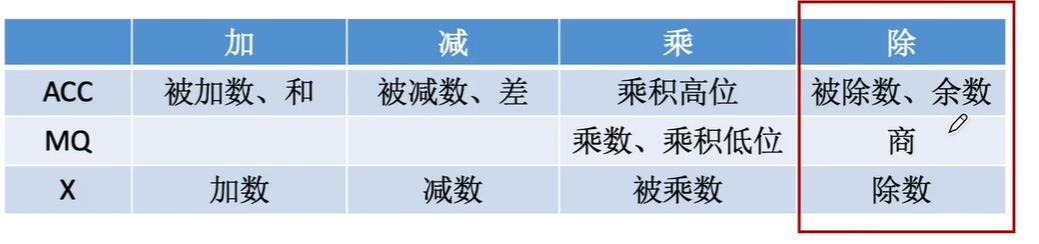
开始的时候,
y
y
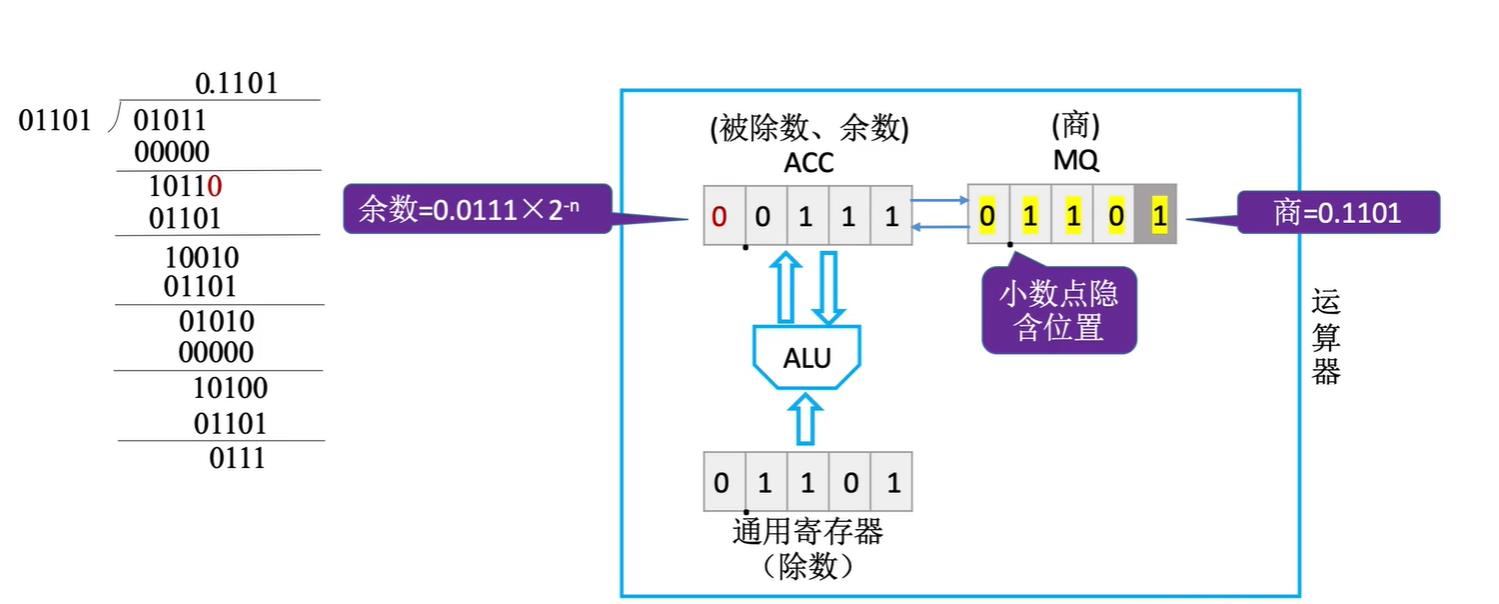
y是除数,位于X寄存器内,ACC寄存器存放的是被除数(x)或余数,MQ中存放商,MQ中灰色加重的方格表示当前要确定的一位商
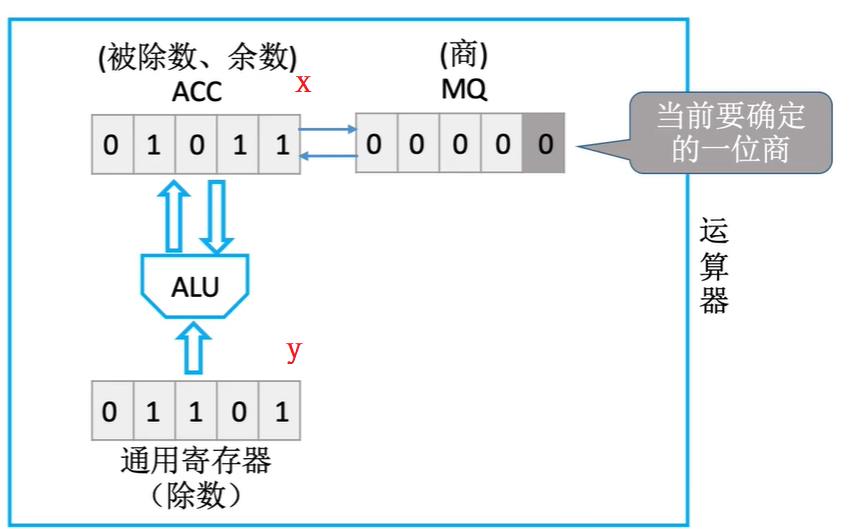
前面手算时,每一位商到底取0还是1,是通过判断当前余数和除数的大小确定的,因此很显然,我们的ACC寄存区和X寄存区天然就存储了余数和除数。但实际情况是,计算机并不会进行比较,它会不管三七二十一直接商1,如果出错再改为商0,并恢复余数
- 商1时,其实就是余数减去除数,也即是
(ACC)-(X)->ACC
于是,这里首先计算机先商1(但是本应该先商0),因此此时就会求余数:(ACC)-(X)->ACC,也即(ACC)+
[
−
∣
y
∣
]
补
[-|y|]_{补}
[−∣y∣]补(计算机依靠加法实现减法),也即
01011
+
10011
=
11110
01011+10011=11110
01011+10011=11110
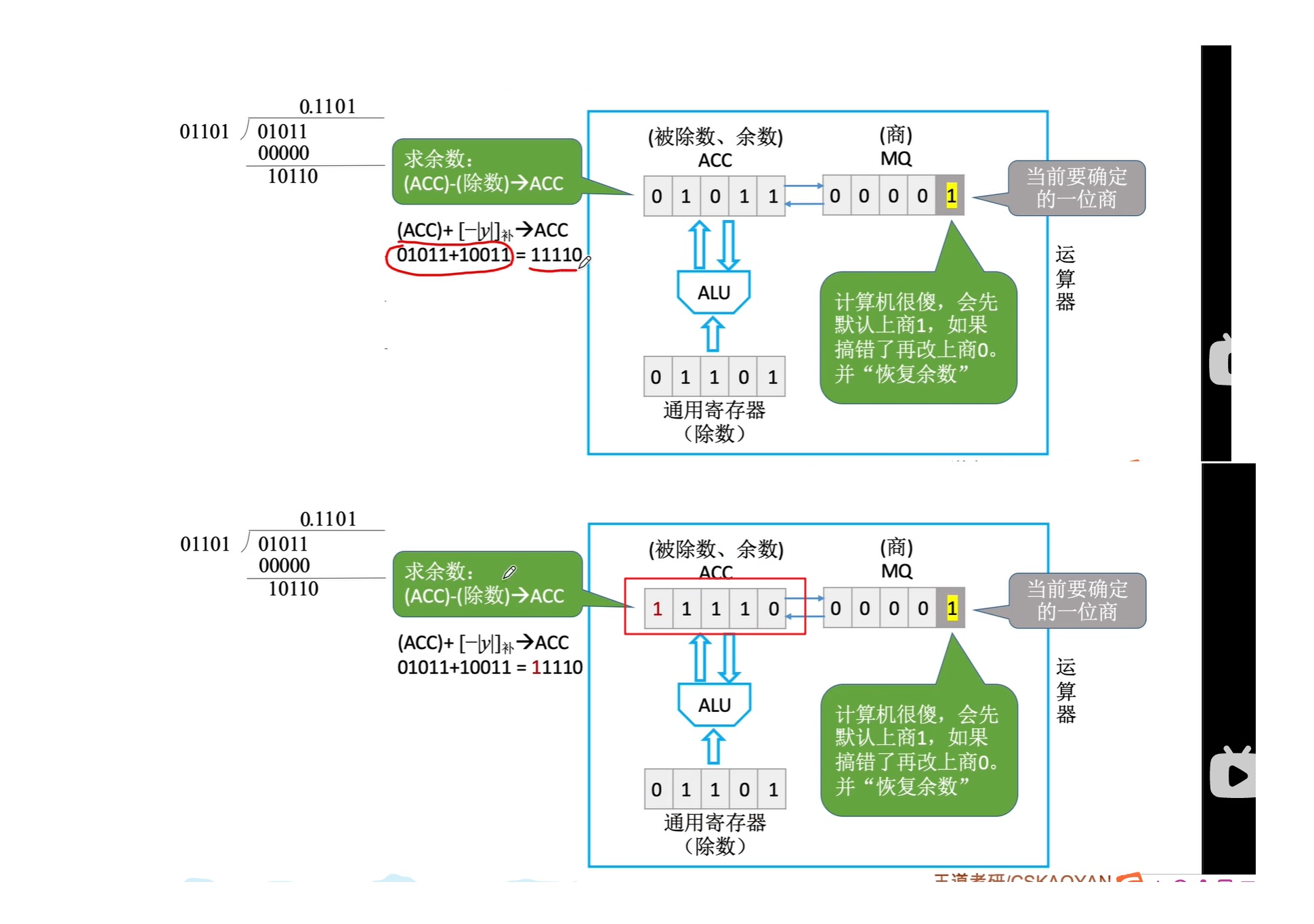
此时符号位1,计算机察觉错误,于是改为商0,同时既然是商0,那么就不应该减去除数,而应该减去0(什么也不做),所以这里直接采取逆过程,加上除数即可
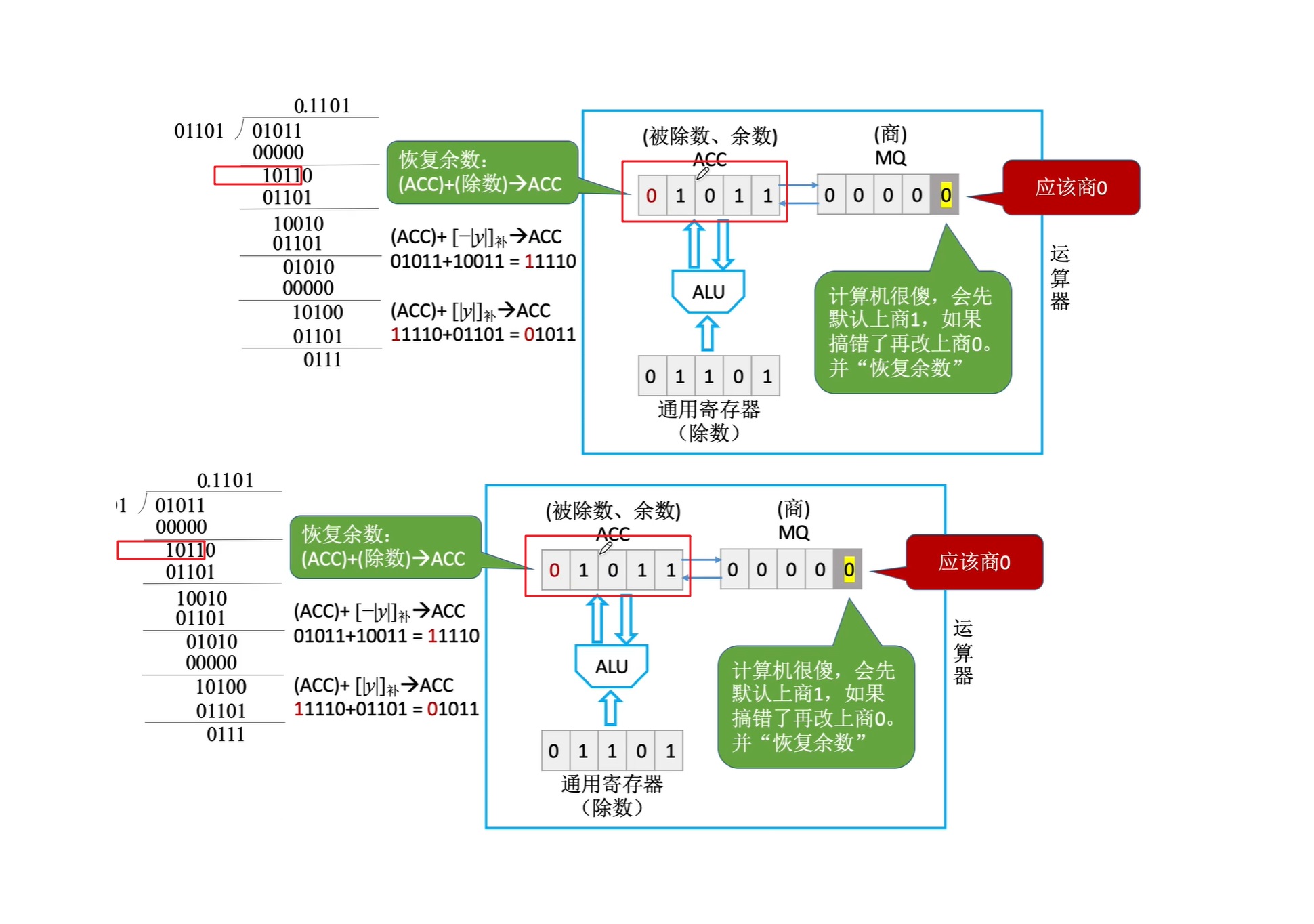
所以现在我们就完成了一位的商,在手算中,我们商完一位后会错位一位补位,然后再商下一位,而在这里对应的就是将ACC和MQ中的内容逻辑左移即可
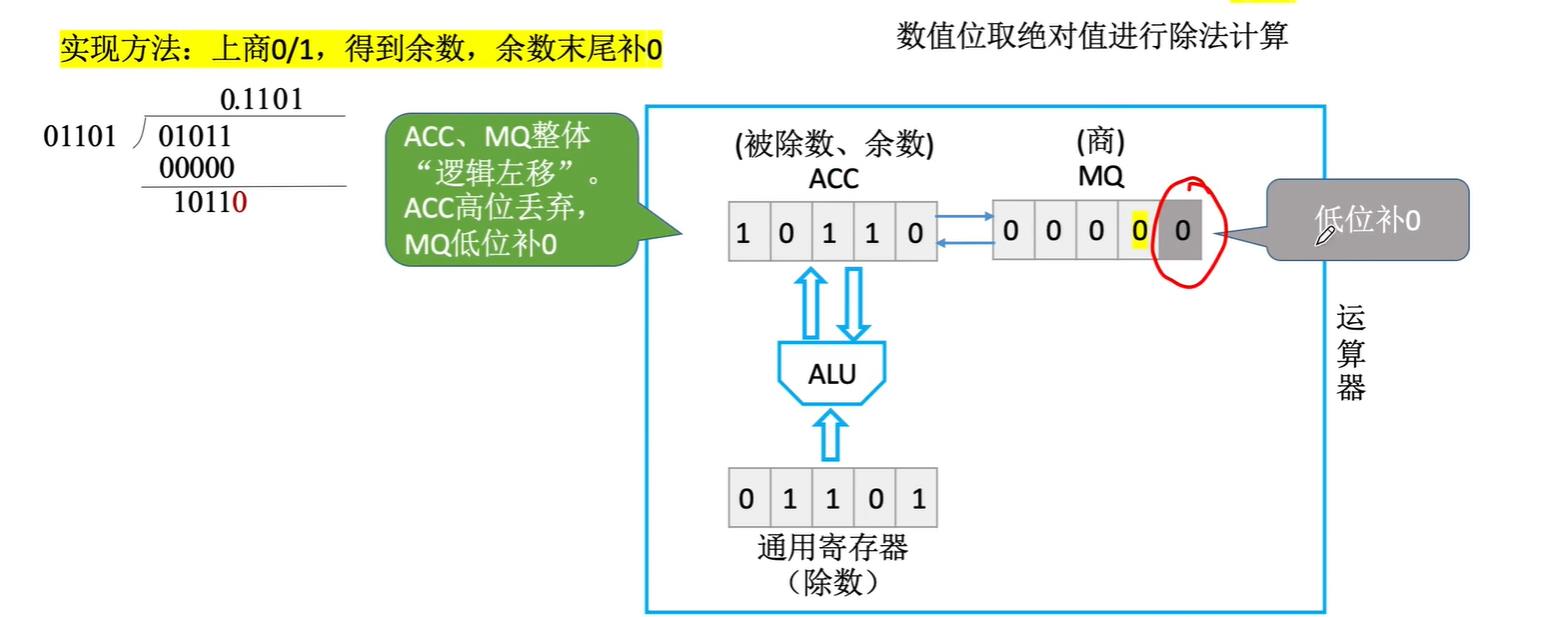
接着计算机再次商1,此时检查符号位为0,说明是正的,说明计算机没有商错误,那么不需要恢复余数
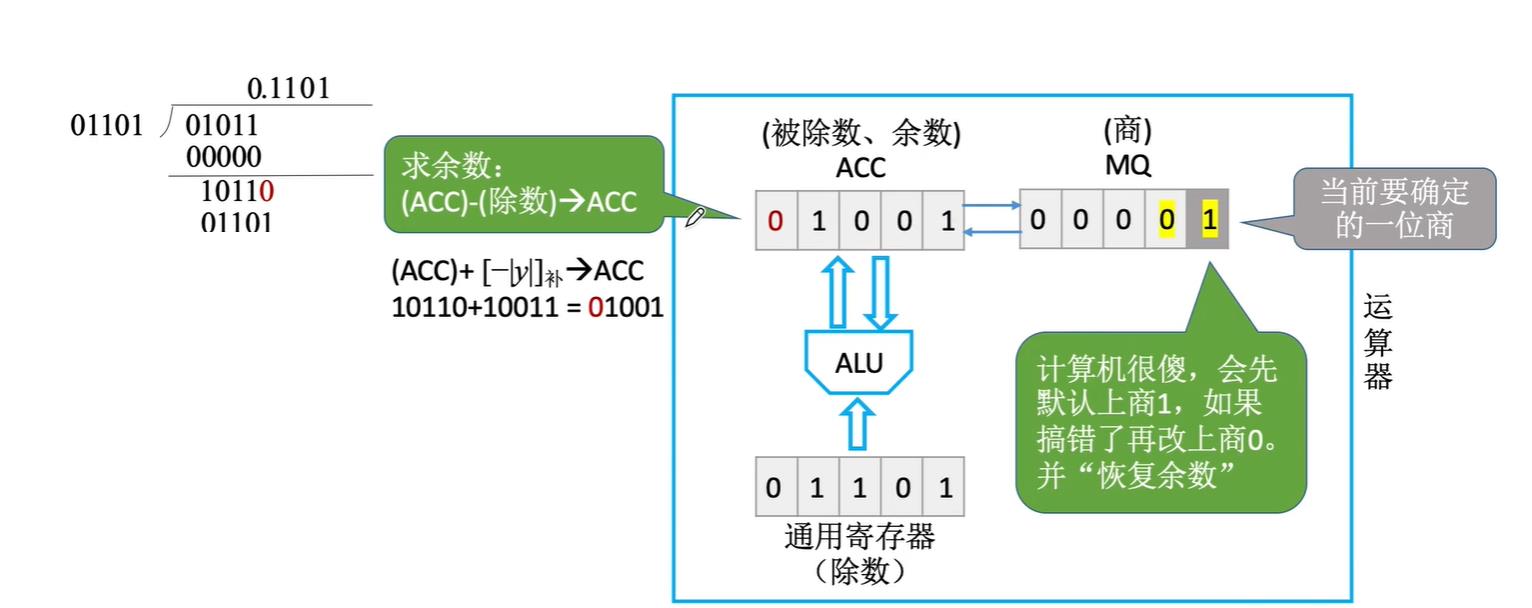
剩下的就是不断左移,运算的过程了。
最后我们假定的机器字长为5位,因此只能求5位的商。不过需要注意的是,如果最后一位商1后,导致了ACC出现负数,那么仍然需要改为0,并恢复余数
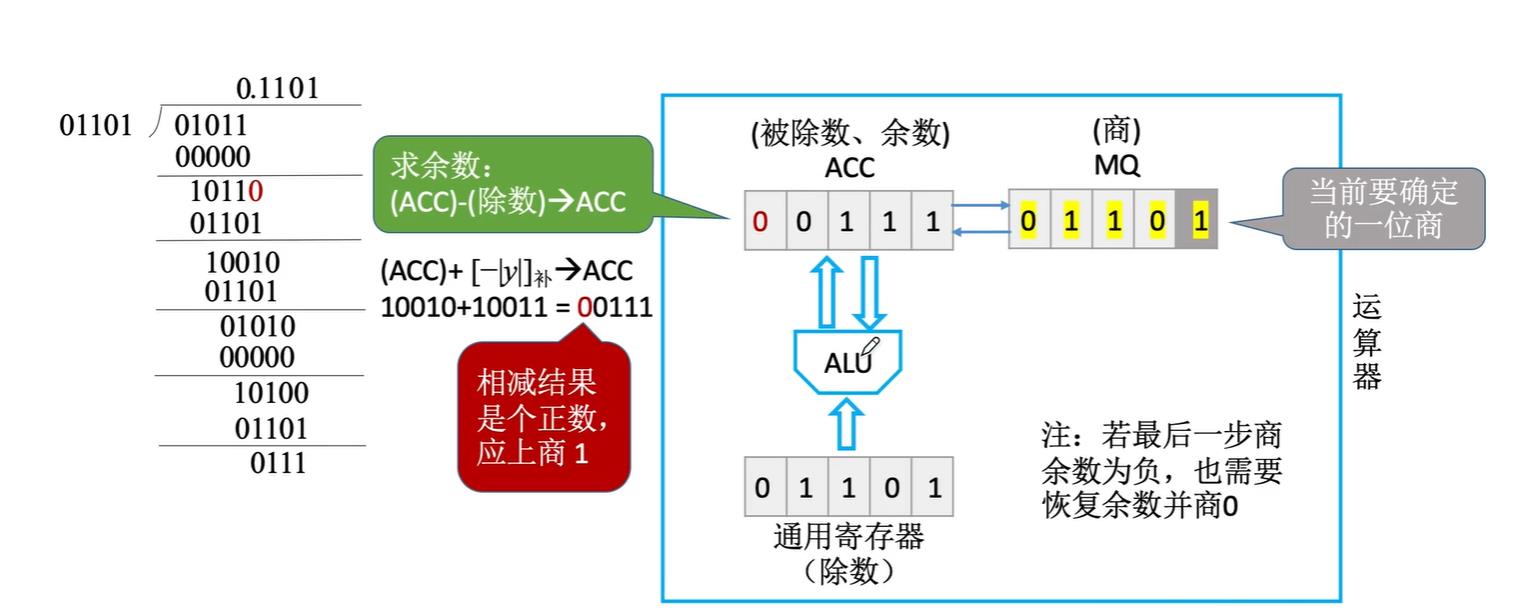
最后,我们这里举的例子是小数,所以其小数点的位置隐含在符号位后面。最后实际的余数是(ACC)×
2
−
n
2^{-n}
2−n(
n
n
n为机器字长)
(2)手算模拟
考试的时候,如果出到这样的题目,具体步骤如下
c
a
s
e
:
case :
case:设机器字长为5位(
n
=
4
n=4
n=4,一位符号位),
x
=
0.1011
x=0.1011
x=0.1011,
y
=
0.1101
y=0.1101
y=0.1101,采用恢复余数法求
x
÷
y
x÷y
x÷y
- ∣ x ∣ = 0.1011 |x|=0.1011 ∣x∣=0.1011
- ∣ y ∣ = 0.1101 |y|=0.1101 ∣y∣=0.1101
- [ ∣ y ∣ ] 补 = 0.1101 [|y|]_{补}=0.1101 [∣y∣]补=0.1101
- [ − ∣ y ∣ ] 补 = 1.0011 [-|y|]_{补}=1.0011 [−∣y∣]补=1.0011

三:原码一位除法:加减交替法(不恢复余数法)
可以看出恢复余数法实际还是挺繁琐的,主要是当余数为负时,它还要加上除数,恢复到上一状态再左移。
而加减交替法是恢复余数的优化,具体规则为:若余数为负,直接商0,并让余数左移1位再加上除数
case : 设 机 器 字 长 为 5 位 ( 设机器字长为5位( 设机器字长为5位(n=4 , 一 位 符 号 位 ) , ,一位符号位), ,一位符号位),x=0.1011 , , ,y=0.1101 , 采 用 恢 复 余 数 法 求 ,采用恢复余数法求 ,采用恢复余数法求x÷y$
- ∣ x ∣ = 0.1011 |x|=0.1011 ∣x∣=0.1011
- ∣ y ∣ = 0.1101 |y|=0.1101 ∣y∣=0.1101
- [ ∣ y ∣ ] 补 = 0.1101 [|y|]_{补}=0.1101 [∣y∣]补=0.1101
- [ − ∣ y ∣ ] 补 = 1.0011 [-|y|]_{补}=1.0011 [−∣y∣]补=1.0011
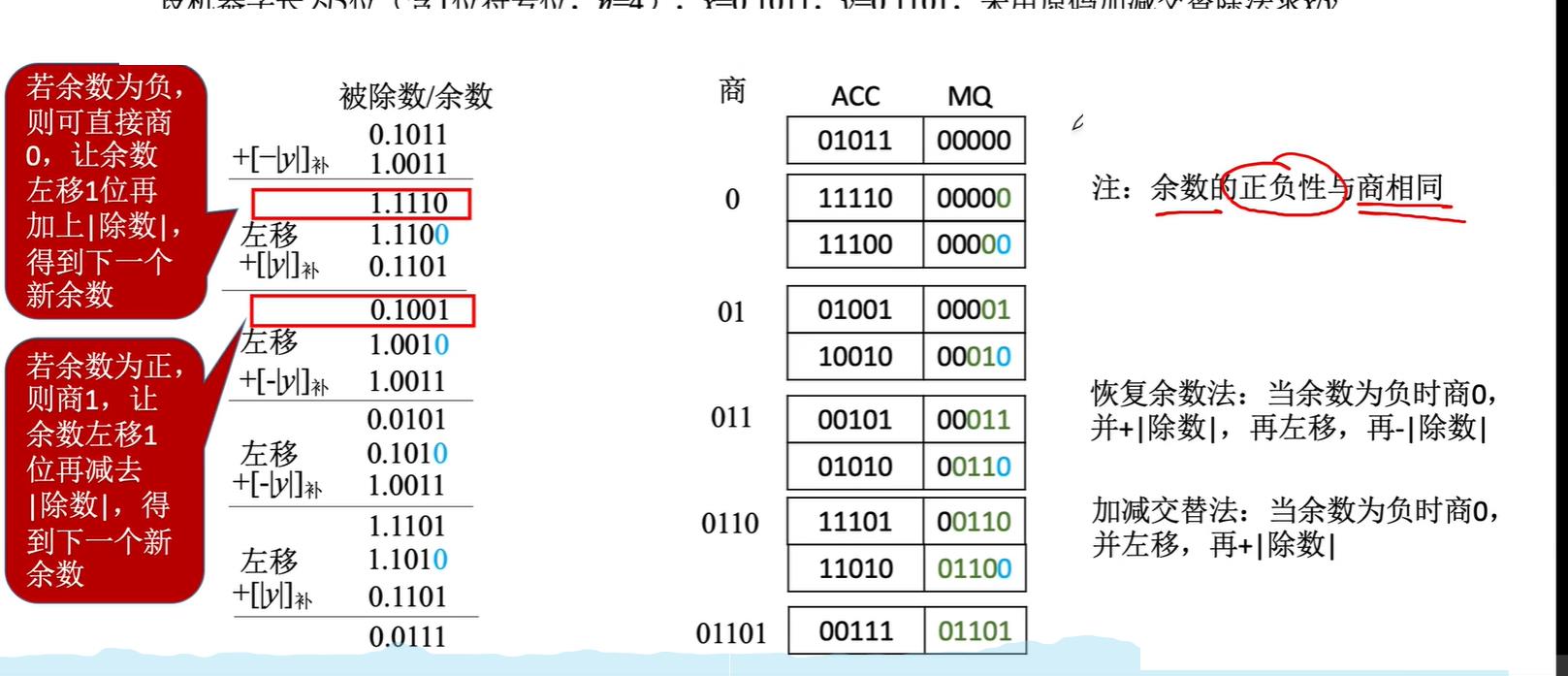
注意:最后一步如果出现负数,仍然需要恢复余数!!!
四:补码一位除法
补码除法采用加减交替法完成,与原码除法的有所区别的是
- 符号位参与运算
- 被除数(余数)、除数采用双符号位
运算的具体细节区别如下
- 原码除法,首先一上来就会让被除数减去除数的绝对值的补码;在补码除法中,若被除数和除数同号,则被除数减去除数,如果异号,则被除数加上除数
- 得到新的余数后判断:若余数和除数同号,则商1,余数左移一位减去除数;若余数和除数异号,则商0,余数左移一位加上除数。
- 在原码除法中如果最后一步余数出现负值,那么需要进行恢复余数;在补码除法中,我们直接把最后一位商置为1即可,这样做很省事,其精度也不会超过 2 − n 2^{-n} 2−n
c a s e : case : case:设机器字长为5位( n = 4 n=4 n=4,一位符号位), + x = 0.1000 +x=0.1000 +x=0.1000, y = − 0.1101 y=-0.1101 y=−0.1101,采用补码加减交替法求 x ÷ y x÷y x÷y
- [ x ] 补 = 00.1000 [x]_{补}=00.1000 [x]补=00.1000
- [ y ] 补 = 11.0101 [y]_{补}=11.0101 [y]补=11.0101
- [ − y ] 补 = 00.1011 [-y]_{补}=00.1011 [−y]补=00.1011
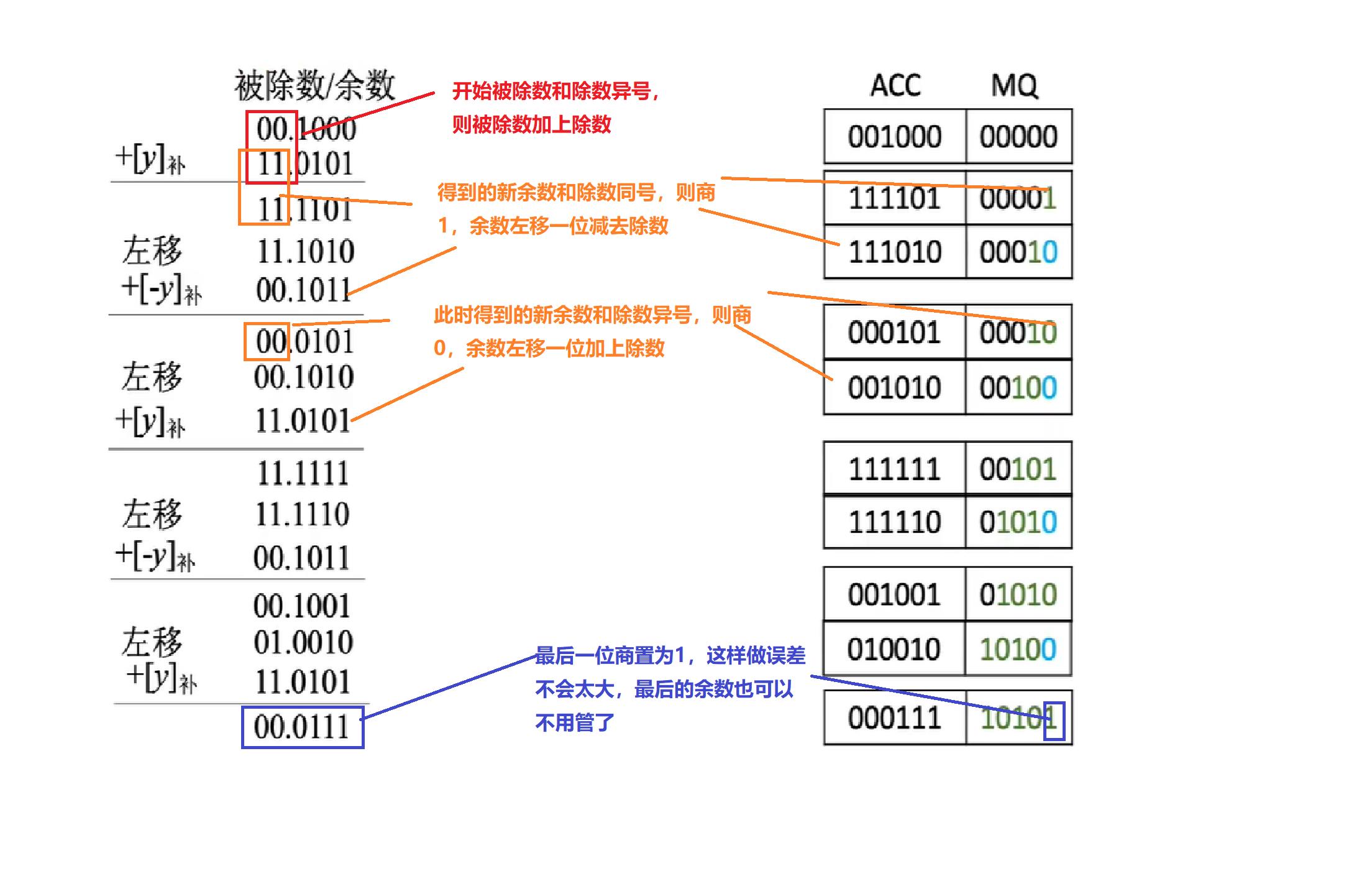
因此最后的结果 [ x / y ] 补 = 1.0101 [x/y]_{补}=1.0101 [x/y]补=1.0101,余数为 0.0111 × 2 − 4 0.0111×2^{-4} 0.0111×2−