Python程序设计 实验2：Python基础练习

Posted 2021-08-31 上山打老虎D

实验2：Python基础练习

• 1. 质数
• • (1)大致思路
  • (2)代码实现
  • (3)运行并测试
• 2. emirp数（prime的反向拼写）
• • (1)大致思路
  • (2)代码实现
  • (3)运行并测试
• 3. 近似平方根
• • (1)大致思路
  • (2)代码实现
  • (3)运行并测试
• 4. 自定义 Triangle 模块
• • (1)大致思路
  • (2)代码实现
  • (3)运行并测试
• 5. 海龟绘图

1. 质数

编写以下两个函数：
1)检查一个整数是否是一个质数：isPrime(number)
2)输出前N个质数：printPrimeNumbers(N)，将输出结果写入文件，命名为 FirstN_Prime_Numbers.txt，N应为相应的数字。

(1)大致思路

①质数判断：
首先判断是否是小于等于1的数字，如果是，则不为质数。其次，使用从2到该数减一的数字依次对这个数字取余，如果余数为零，即这个数存在非1与自己本身的因子。该数字即不为质数。否则即为质数。
②输出并读写文件：
使用文件流创建对应名字的文件，并清零计数器。每生成一个质数，通过输出流写入文件中并计数器加一，直至计数器达到n并跳出循环。

(2)代码实现

# 定义判断质数函数  
def isPrime(number):  
    if number <= 1:  
        return False  
    for i in range(2, number - 1):  
        if number % i == 0:  
            return False  
    return True  
  
  
# 获取n的输入  
n = eval(input("Please input a number:"))  
# 通过输出流创建对应文件  
myFile = open("First"+str(n)+"_Prime_Numbers.txt", "w")  
count = 0  
num = 0  
  
# 循环获取质数，并存入文件中  
while count < n:  
    num += 1  
    if isPrime(num):  
        count += 1  
        myFile.write(str(num)+"\\n")  

首先，定义判断质数函数，先判断是否是小于等于1的数字，如果是，则不为质数。其次，使用从2到该数减一的数字依次对这个数字取余，如果余数为零，即这个数存在非1与自己本身的因子。该数字即不为质数。否则即为质数。
获取了n的输入之后，使用文件流创建对应名字的文件，并清零计数器。每生成一个质数，通过输出流写入文件中并计数器加一，直至计数器达到n并跳出循环。

(3)运行并测试

①开始运行，程序将提示输入一个数字n

②我们输入20，并敲击回车之后程序将开始执行。

我们可以看到，已经生成了对应的结果文件。
打开文件后可以发现，结果被正确的写入到文件中。

2. emirp数（prime的反向拼写）

emirp数是一种特殊的质数，它反向书写时也是一个质数。例如，17和71都是质数，所以17和71都是emirp数。编写一个函数emirp(N)，输出前N个emirp数到文件中，每行最多显示10个数字，如下所示。文件命名为FirstN_Emirp_Numbers.txt，N应为相应的数字。

13 17 31 37 71 73 79 97 107 113
149 157 167 179 199 311 337 347 359 389
…

(1)大致思路

①质数判断：
首先判断是否是小于等于1的数字，如果是，则不为质数。其次，使用从2到该数减一的数字依次对这个数字取余，如果余数为零，即这个数存在非1与自己本身的因子。该数字即不为质数。否则即为质数。
②数字翻转：
可以先将数字转为字符串，并将字符串翻转之后再转为int型
③输出并读写文件：
使用文件流创建对应名字的文件，并清零计数器。每生成一个质数，通过输出流写入文件中并计数器加一，直至计数器达到n并跳出循环。
④换行处理：
可以通过每次输出时对计数器进行对10的取余，即完成每10个数一换行。

(2)代码实现

# 定义判断质数函数  
def isPrime(number):  
    if number <= 1:  
        return False  
    for i in range(2, number - 1):  
        if number % i == 0:  
            return False  
    return True  
  
  
# 定义数字翻转函数  
def reverse(n):  
    s = str(n)  # 转为字符串  
    s = s[-1::-1]  # 字符串反转  
    n = int(s)  # 转为数字  
    return n  
  
  
# 定义emirp函数  
def emirp(n):  
    # 通过输出流创建文件  
    myFile = open("First" + str(n) + "_Emirp_Numbers", "w")  
    count = 0  
    num = 0  
    # 循环获取质数，并存入文件中  
    while count < n:  
        num += 1  
        if isPrime(num) and isPrime(reverse(num)) and num != reverse(num):  
            count += 1  
            myFile.write(str(num) + " ")  
            # 如果已经十个数字则换行  
            if count % 10 == 0:  
                myFile.write("\\n")  
  
  
# 获取n的输入  
n = eval(input("Please input a number:"))  
emirp(n) 

首先，定义emirp判断函数，分别对数字进行判断，只有原数字与转置数字不相等也都为质数的情况下才满足条件并将数字输出到文件中。
获取了n的输入之后，使用文件流创建对应名字的文件，并清零计数器。每生成一个质数，通过输出流写入文件中并计数器加一，直至计数器达到n并跳出循环。
每次输出的时候将计数器对10进行取余完成每10个数字换一次行。

(3)运行并测试

①开始运行，程序将提示输入一个数字：

②输入结束之后程序完成运行，可以看到对应文件已经被创建了。



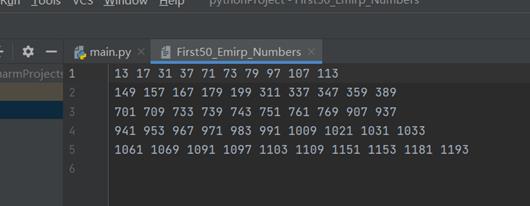
而且也实现了每十个数字换行一次。

3. 近似平方根

有几种方法可以实现 Python math 模块中的 sqrt 函数，其中一种方法被称为巴比伦函数法。它使用以下公式，不断逼近一个数 n 的平方根
$$nextGuess=\frac{lastGuess+\frac{n}{lastGuess}}{2}$$
当 nextGuess 和 lastGuess 几乎相同时，nextGuess 就是近似平方根。初始猜测，即 lastGuess 的起始值，可以是任何正值（例如 1）。如果 nextGuess 和 lastGuess的差小于一个非常小的数字，例如 0.0001，那么可以说 nextGuess 是 n 的近似平方根，如果不是，则 nextGuess 变为 lastGuess，近似过程继续。根据以上方法，实现返回 n 的平方根的函数 my_sqrt(n)。

(1)大致思路

通过while循环，进行每次计算，并对每次循环结果与上次循环做差进行判断，如果在阈值以内则跳出循环并返回，否则更新当前结果，并继续循环。

(2)代码实现

# 定义开方函数  
def mySqrt(num):  
    # 赋初值  
    lastGuess = 1  
    # 利用循环进行判断  
    while True:  
        nextGuess = (lastGuess + (num / lastGuess)) / 2  
        # 如果小于阈值则返回  
        if abs(nextGuess - lastGuess) < 1e-5:  
            return nextGuess  
        # 继续运算  
        lastGuess = nextGuess  
  
  
# 获取输入  
num = eval(input("Please in put a number:"))  
print(mySqrt(num))  

首先定义初始值，并通过while循环进行每次运算，通过if对每次循环的结果进行判断，如果两次运行的差的绝对值小于阈值，则将结果返回，否则继续进行循环运算直至两次运行的差的绝对值小于阈值。
接受输入后调用函数并将结果输出。

(3)运行并测试

①运行程序，将提示输入一个数字：

②输入完成后即可看到计算出的平方根结果

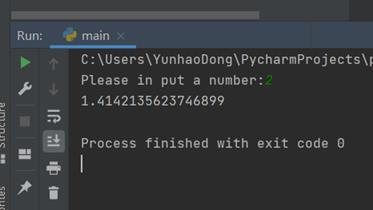
4. 自定义 Triangle 模块

编写一个模块 Triangle，包含以下三个函数：

1. isValid(side1, side2, side3): 输入三条边长度，判断是否组成三角形；
2. perimeter(side1, side2, side3): 输入三条边长度，求三角形周长；
3. area(side1, side2, side3): 输入三条边长度，求三角形面积。
   自行设计主程序验证模块是否编写正确。

(1)大致思路

①isValid(side1, side2, side3)
先判断三边长度是否为大于零的数值，如果假则返回false。再通过对三条边进行两边之和是否大于第三边。如都满足则返回true，否则返回false。
②perimeter(side1, side2, side3)
直接返回三边长度之和即可
③area(side1, side2, side3)
可以通过海伦公式计算面积并返回：
$$S=\sqrt{(p\ast (p-a)\ast (p-b))\ast (p-c)}$$
其中，p为半周长，a,b,c分别为三边长度。

(2)代码实现

Triangle.py：
在模块文件中定义三角形的各个函数。

# 判断能否构成三角形  
def isValid(a, b, c):  
    if a <= 0 or b <= 0 or c <= 0:  
        return False  
    if a+b <= c:  
        return False  
    if a+c <= b:  
        return False  
    if c+b <= a:  
        return False  
    return True  
  
  
# 获取周长函数  
def perimeter(a, b, c):  
    return a+b+c  
  
  
# 获取面积函数  
def area(a, b, c):  
    # 海伦公式  
    p = (a+b+c)/2  
    return (p*(p-a)*(p-b)*(p-c))**0.5  

主函数：

# 引入自定义三角形模块  
import Triangle  
  
# 获取输入  
a = eval(input("Please input the first number: "))  
b = eval(input("Please input the second number: "))  
c = eval(input("Please input the third number: "))  
if Triangle.isValid(a, b, c):  
    # 如果是三角形则计算周长和面积  
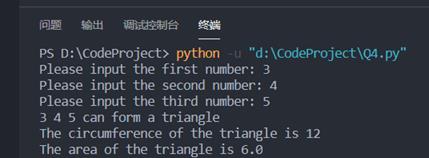
    print(a, b, c, "can form a triangle")  
    print("The circumference of the triangle is", Triangle.perimeter(a, b, c))  
    print("The area of the triangle is", Triangle.area(a, b, c))  
else:  
    # 输出不能组成三角形的信息  
    print(a, b, c, "cannot form a triangle")  

首先引入三角形模块，获取了三边长度的输入之后对三边长度进行判断，如果不能构成三角形，则给出提示信息。如果能构成三角形则给出提示信息的同时输出三角形的周长和面积。

(3)运行并测试

①如果输入的数据不能构成三角形，则给出提示：

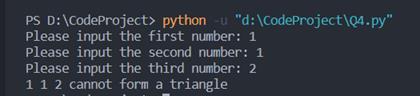
5. 海龟绘图

自学 Python 自带的 turtle 模块，完成以下两个任务：
1)仔细阅读代码 exp2.5_example.py 并运行，回答以下问题：
A. 运行代码后，你看到了什么？
运行代码后可以看到一个小人发射出爱心的图形：

B. 解释以下函数的含义：
up(), down(), goto(), circle(), forward(), right(), left(), speed()
①up()
将画笔抬起，移动时不画线

②down()
将画笔落下，移动时画线

③goto()
goto(x, y=None)
其中，x为一个数值或数值对/向量，y为可缺省的一个数值。
如果 y 缺省，x 应为一个表示坐标的数值对或 Vec2D 类对象 (例如 pos() 返回的对象).
此函数将海龟移动到一个绝对坐标。如果画笔已落下将会画线。不改变海龟的朝向。
例如：

tp = turtle.pos()
tp
(0.00,0.00)
turtle. goto (60,30)
turtle.pos()
(60.00,30.00)

④circle()
turtle.circle(radius, extent=None, steps=None)
参数
radius：一个数值，表示半径
extent – 一个可缺省数值表示作图角度
steps – 一个可缺省整型数，表示做多边形边数
绘制一个 radius 指定半径的圆。圆心在海龟左边 radius 个单位；extent 为一个夹角，用来决定绘制圆的一部分。如未指定 extent则绘制整个圆。如果 radius 为正值则朝逆时针方向绘制圆弧，否则朝顺时针方向。最终海龟的朝向会依据 extent 的值而改变。
圆实际是以其内切正多边形来近似表示的，其边的数量由 steps 指定。如果未指定边数则会自动确定。此方法也可用来绘制正多边形。
a. 若extent和steps都缺省则直接做完整的圆：

import turtle  
turtle.circle(100)  
turtle.done() 

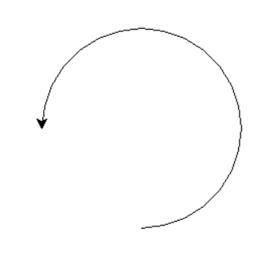
b.若steps缺省则做不完整的圆，extend值表示做圆的所对圆心角：

import turtle  
turtle.circle(100,270)  
turtle.done()  

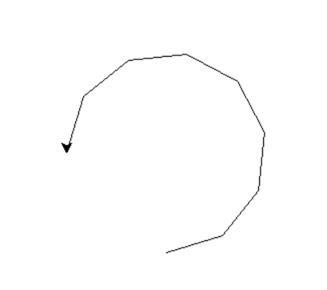
c. 若都不缺省，则做以steps为边数的，以extend为角度的多边形

⑤forward()
forward(distance)
distanc为一个数值 (整型或浮点型)。表示海龟前进 distance 指定的距离，方向为海龟的朝向。
例如：

turtle.position()
(0.00,0.00)
turtle.forward(25)
turtle.position()
(25.00,0.00)

⑥right()
right(angle) angle为一个数值 (整型或浮点型)
海龟右转angle个单位。
例如：

turtle.heading()
22.0
turtle.right(45)
turtle.heading()
337.0

⑦left()
turtle.left(angle) angle为一个数值 (整型或浮点型)

turtle.heading()
22.0
turtle.left(45)
turtle.heading()
67.0

⑧speed()
speed(speed=None)
参数：speed为一个 0~10 范围内的整型数或速度字符串
如果设置海龟移动的速度为 0~10 表示的整型数值。如未指定参数则返回当前速度。
如果输入数值大于 10 或小于 0.5 则速度设为 0。速度字符串与速度值的对应关系如下:
“fastest”: 0 最快
“fast”: 10 快
“normal”: 6 正常
“slow”: 3 慢
“slowest”: 1 最慢
速度值从 1 到 10，画线和海龟转向的动画效果逐级加快。
例如：

turtle.speed()
3
turtle.speed(‘normal’)
turtle.speed()
6
turtle.speed(9)
turtle.speed()
9

2)用 turtle 模块作出一幅你满意的画。
我们要通过Python自带的turtle包画一个八卦的样子：
①首先定义画笔，并进行填充

import turtle  
turtle.speed(10)  
turtle.pensize(4)  
  
turtle.color('black', 'black')  
turtle.begin_fill()  

②画出右侧中间的圆

# 右侧中圆  
turtle.circle(50, 180)  

③画出左侧大圆

# 左侧大圆  
turtle.circle(100, 180)

④画出左侧中圆

# 左侧中圆  
turtle.left(180)  
turtle.circle(-50, 180)  
turtle.end_fill()  
  
turtle.color('white', 'white')  
turtle.begin_fill()  

⑤画出上面的小圆

# 上小圆  
turtle.left(90)  
turtle.penup()  
turtle.forward(35)  
turtle.right(90)  
turtle.pendown()  
turtle.circle(15)  
turtle.end_fill()  
turtle.color('black', 'black')  
turtle.begin_fill() 

⑥画出下面的小圆

# 下小圆  
turtle.left(90)  
turtle.penup()  
turtle.backward(70)  
turtle.pendown()  
turtle.left(90)  
turtle.circle(15)  
turtle.end_fill() 

⑦画出右侧大圆

# 右大圆  
turtle.right(90)  
turtle.up()  
turtle.backward(65)  
turtle.right(90)  
turtle.down()  
turtle.circle(100, 180)  
  
turtle.done()  

运行并展示最终效果如下