[人工智能-深度学习-3]:张量tensor是数组Aarry和矩阵Matrix的泛化
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[人工智能-深度学习-3]:张量tensor是数组Aarry和矩阵Matrix的泛化相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119358616
目录
第1章 张量的定义
1.1 张量在深度学习中的定义
张量(tensor)是多维数组,是向量、矩阵推向更高的维度的一种统一的、抽象的概念。
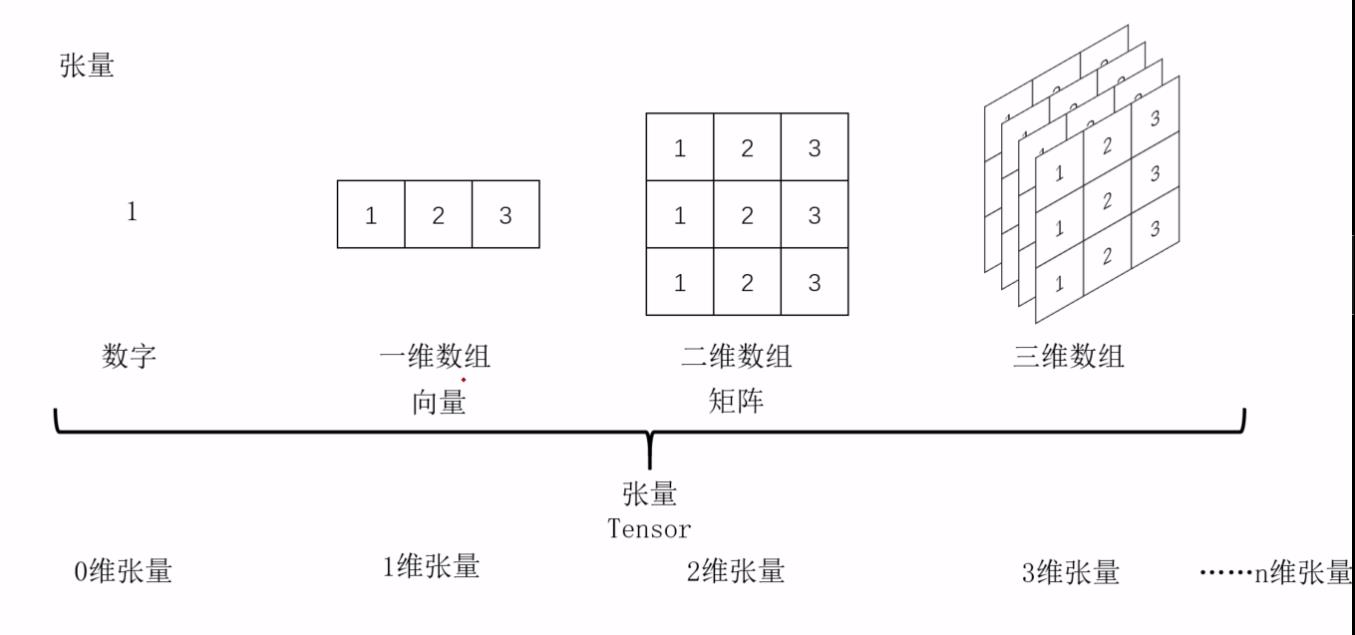
n维向量:1维张量,在该维度包含n个分量,这就是n维向量,n为向量是1维的张量。
1维张量:有L个元素组成。
2维张量:有n*m个元素组成。
3维张量:有x*y*z个元素组成。每个维度方向,都是一个完整的数据集。
因此,在Python中,张量就是Python Numpy中的多维数组。
1.2 张量的应用
在深度学习领域,用张量这样一个新的概念,替代Python Numpy中的0维张量(标量)、一维的向量,二维的矩阵,高维的数组。
在深度学习框架中,所有待进行数学运算的数据,都是以张量的形态存储、存在。
任何维度的数据,如果不是张量形态的数据,需要首先转换成张量的形态。
1.3 为什么需要张量呢?
这是因为,在深度学习领域,输入的数据、深度学习处理的数据、输出数据,它们的维度为弹性的,并非确切的,因此需要一种弹性的数据来描述各种类型的数据,张量应运而生。
1.4 张量的本质
如果说向量是一种有m个特征的一维的数据结构,如身高、体重、地区、性别,
那么张量把这些特征,进行分组,每一个组称为一个维度,构成了一个多维特征的数据结构,这个数据结构就称为张量,因此张量是组织众多特征的一种数据结构!!!
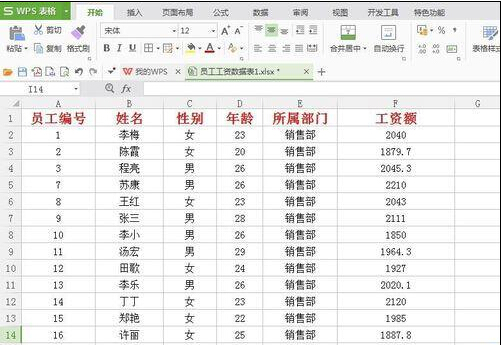
上述定义的excel表格与张量有这本质的区别:
excel表格的“列”是特征,上述表格中,特征是以一维向量的形式组织的。
excel表格的行是数据,每一行就是一个满足上述特征的数据实例,一个实例就是一个数据样本,行数可以无限多,样本可以无限多。
如果把上述表格中的特征,进行分组,便可构成二维、三维、高维的特征值,这便是张量!
张量是管理任意维度“特征”的一种数据结构。
第2章 张量的算数运算
张量的算术运算,就是多维数组的数学运算。
[Python系列-12]:人工智能 - 数学基础 -2- 数组元素的算术运算
https://blog.csdn.net/HiWangWenBing/article/details/119298635
第3章 张量的形状运算
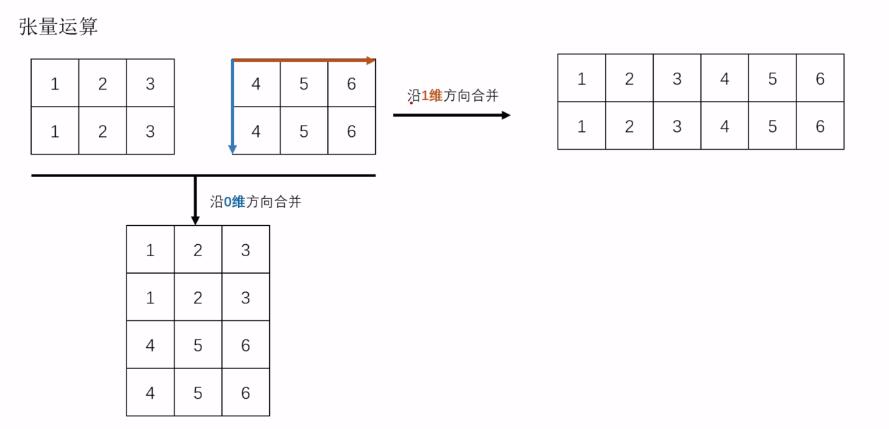
3.1 合并
备注:
0维度方向:是指沿着行扩展的方向,增加或扩展行数的方式来合并。
1维度方向:是指沿着列扩展的方向,增加或扩展列数的方式来合并。
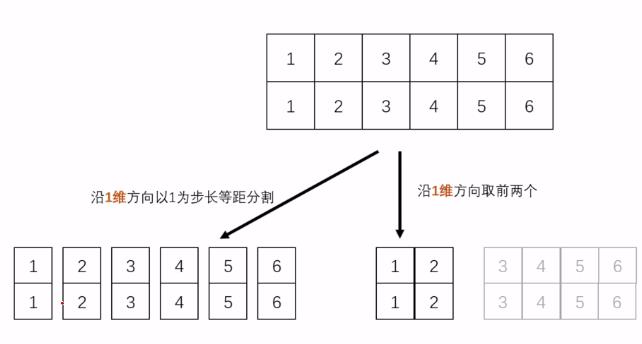
3.2 张量的分解
第4章 点积与乘积
4.1 张量的点积/内积
张量的点积就是多维数组的点积:
[Python系列-15]:人工智能 - 数学基础 -5- 向量内积(点乘)和外积(叉乘)概念及几何意义
https://blog.csdn.net/HiWangWenBing/article/details/119322764
4.2 张量的乘积/外积 (深度学习用不到)
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119358616
以上是关于[人工智能-深度学习-3]:张量tensor是数组Aarry和矩阵Matrix的泛化的主要内容,如果未能解决你的问题,请参考以下文章