并查集的学习和模拟实现

Posted 2021-08-30 zhaocx111222333

并查集

将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集。

采用了类似于森林的数据形式。

特点：
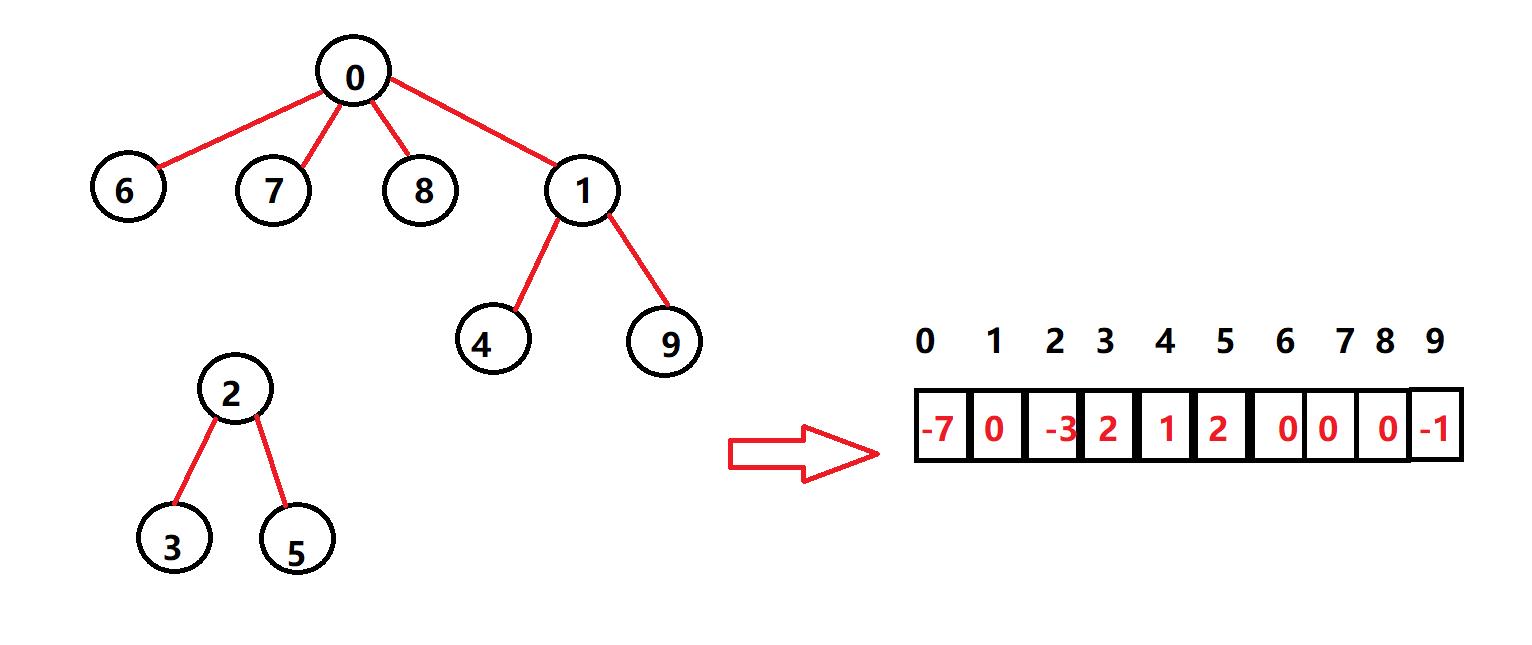
1.初始化为-1；
2.在一组的数据选出一个代表当根节点，根节点用负数存储该集合的元素个数
3.集合的其他节点存根节点的索引。
4.将两个数据加入到一个结合，要先判断它们的顶级跟集合是否在一起，在一起则结束，若不在一起需要将两个根节点再次构造为一个集合（被选为子节点的根节点的子节点不变）
图示：

#include<vector>
using namespace std;
class UnionFindSet
{
public:										// 初始时，将数组中元素全部设置为-1
	UnionFindSet(size_t size)
		: _ufs(size, -1)
	{}
											
	int FindRoot(int index){				// 给一个元素的编号，找到该元素所在集合的名称											
		while (_ufs[index] >= 0){			// 根据下标拿到内容	
			index = _ufs[index];
		}
		return index;						//得到根集合的索引
	}

											
	bool Union(int x1, int x2){				//将两个内容插入一个集合
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);			
		if (root1 == root2)					// x1已经与x2在同一个集合
			return false;					// 将两个集合中元素合并（两个负数相加）
		_ufs[root1] += _ufs[root2];			//只有根节点变了，这个变化的根节点的字节的跟还是他
		_ufs[root2] = root1;				// 将其中一个集合名称改变成另外一个（随便指定一个根集合	
		return true;
	}
											// 数组中负数的个数，即为集合的个数
	size_t Count()const{
		size_t count = 0;
		for (auto e : _ufs){
			if (e < 0)
				++count;
		}
		return count;
	}
private:
	vector<int> _ufs;
};

并查集-等式方程可满足性

    class BCJ{
    public:
    BCJ(int size):v(size,-1){}
    int getroot(int point){
        while(v[point]>=0){
            point=v[point];
        }
        return point;
    }

    bool Union(int a,int b){
        int roota=getroot(a);
        int rootb=getroot(b);
        if(roota==rootb){return false;}
        v[roota]+=v[rootb];
        v[rootb]=roota;
        return true;
    }

    private:vector<int> v;
};
class Solution {
public:
    
    bool equationsPossible(vector<string>& equations) {
        if(equations.size()==0){return false;}
        BCJ b(26);
        for(auto &i:equations){
            if(i[1]=='='){
                b.Union(i[0]-'a',i[3]-'a');
            }
        }
        for(auto &i:equations){
            if(i[1]=='!'){
                int roota=b.getroot(i[0]-'a');
                int rootb=b.getroot(i[3]-'a');
                if(roota==rootb){return false;}
                
            }
        }
        return true;
    }
    
};