Splay树（21.8.1）

Posted 2021-08-30 未定_

一、Splay树
1.Splay树是一种BST树，允许查找、插入、删除、分割、合并等操作。
2 Splay树的原理: 为了使整个查找时间更少，被查频率高的那些结点应当经常处于靠近树根的位置。Splay树可以通过旋转的方式把被访问结点旋转到树根的位置以减少查找时间。
3.与Treap树的不同:
•Splay树允许把任意结点旋转到树根，Treap树形态固定所以不能。
•Splay树分裂、合并更简便。

二、Splay树的操作
1.提根(把结点x旋转到根)
•x的父结点是根，只需旋转一次。x是左儿子则右旋，反之左旋，且前后中序顺序不变。
•x的父结点不是根，但x、x的父结点、x的父结点的父结点三点共线，则先旋转x的父结点，再旋转x。

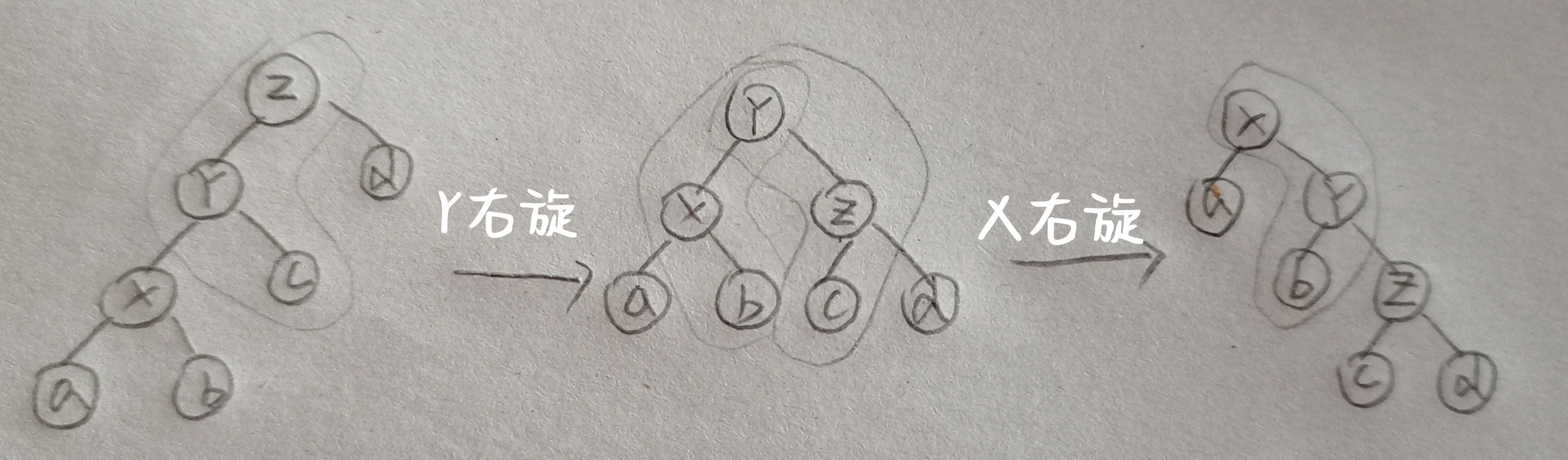
•x、x的父结点、x的父结点的父结点三点不共线，把x按不同方向旋转两次。

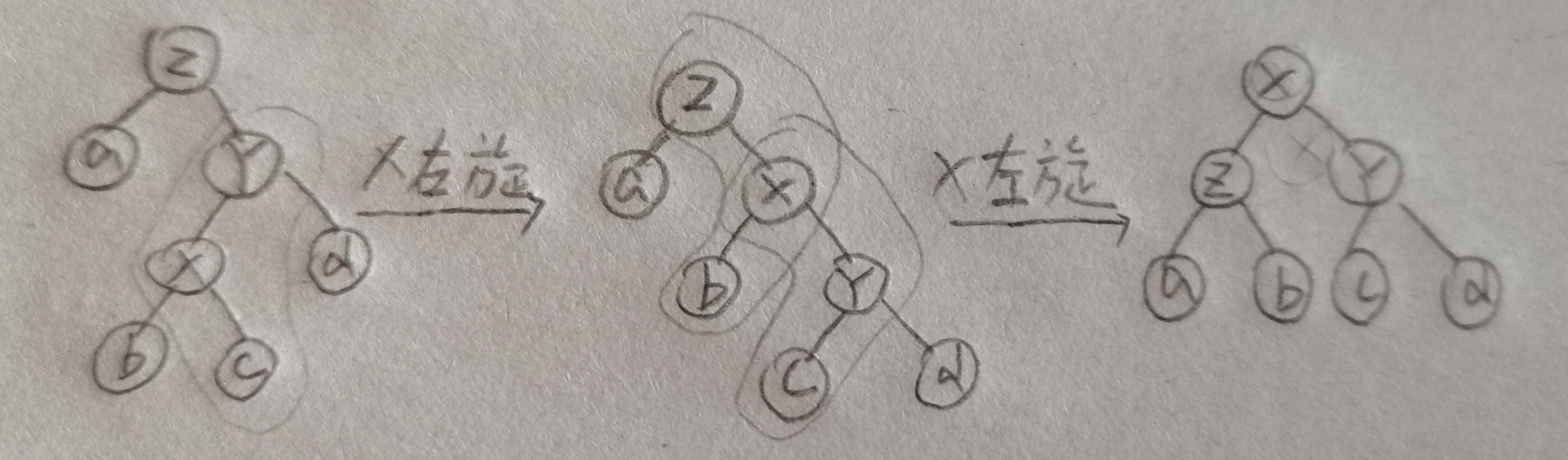
2.插入: 同BST树的插入
3.删除: 待删结点旋转到根，删除，合并左右子树。
4.合并: 只有left树的所有元素都小于right树的所有元素从可以合并。先把left最大元素x旋转到树根，再把x的右子树接到right上。
5.分裂: 把第k小的元素旋转到树根，然后把它与右子树断开即可。
6.查找x: 把x旋转到根结点
•查找最大、最小、第k大的数。用中序遍历查找，查找后把它旋转到根。

模板题：Robotic Sort
题意：给物品排序，按照以下方式翻转： 先找到编号最小的物品的位置P1，将区间[1,P1]反转，再找到编号第二小的物品的位置P2，将区间[2,P2]反转……
已知个数n和编号，求出所有的Pi。
一下代码包含：提根、插入、删除、得最大值等操作。

#include<bits/stdc++.h>
using namespace std;
const int maxn=100010;
int root;//根
int rev[maxn],pre[maxn],size[maxn];//rev[i]标记i被翻转；pre[i]i的父结点；size[i]i的子树上结点的个数
int tree[maxn][2];//记录树：tree[i][0],i的左儿子，tree[i][1],i的右儿子
struct node
{
    int val,id;//val是编号，id是编号的位置
    bool operator <(const node &A)const//用于sort排序，先按编号从小到大排，再按编号的位置从小到大排
    {
        if(val==A.val)
            return id<A.id;
        return val<A.val;
    }
} nodes[maxn];//有多个结点
void pushup(int x)//计算以x为根的子树包含多少个子结点
{
    size[x]=size[tree[x][0]]+size[tree[x][1]]+1;//左子树+右子树+1(本身)
}
void update_rev(int x)//标记翻转的结点x，x表示id也就是编号val所在的位置
{
    if(!x)//x为0就退出
        return;
    swap(tree[x][0],tree[x][1]);//翻转x:交换x的左右儿子
    rev[x]^=1;//标记x被翻转，这里相当于rev[x]=rev[x]^1，0^1=1，1^1=0
}
void pushdown(int x)//根据本题需要，处理机械臂翻转(题)
{
    if(rev[x])//如果翻转过
    {
        update_rev(tree[x][0]);//标记翻转的x的左儿子
        update_rev(tree[x][1]);//标记翻转的x的右儿子
        rev[x]=0;//x本身的左右儿子没有被交换，x没翻转再变成0
    }
}
void Rotate(int x,int c)//旋转x，c=0为左旋，c=1为右旋
{
    int y=pre[x];//y=x的父结点
    pushdown(y);//机械臂翻转父结点
    pushdown(x);//机械臂翻转x自己
    tree[y][!c]=tree[x][c];//左旋时，x的左儿子变成父结点y的右儿子；右旋时，x的右儿子变成父结点y的左儿子
    pre[tree[x][c]]=y;//左旋时，x的父结点y变成x的左儿子的父结点，即左儿子父结点变成y;右旋时，x的父结点y变成x的右儿子的父结点，即右儿子父结点变成y
    if(pre[y])//如果y的父结点存在，要让x取代y，建立y的父结点与x的联系，目的是让y的父结点的儿子变成x
        tree[pre[y]][tree[pre[y]][1]==y]=x;//第一个[]里pre[y]表示y的父结点，第二个[]里tree[pre[y]][1]==y用来判断y是否为y的父结点的右儿子，这里tree[][]总得意义就是让y的父结点的儿子变成x，即用x取代y的位置
    pre[x]=pre[y];//建立x与y的父结点的联系，目的是让x的父结点变成y的父结点(无论有没有)
    tree[x][c]=y;//左旋时，y变成x的左儿子；右旋时，y变成x的右儿子
    pre[y]=x;//x变成y的父结点
    pushup(y);//计算以y为根的子树包含多少个子结点
}
void splay(int x,int goal)//把结点x旋转为goal的儿子，如果goal是0，则旋转到根
{
    pushdown(x);//对x做机械臂翻转
    while(pre[x]!=goal)//如果x没旋转到goal的儿子就一直旋转
    {
        if(pre[pre[x]]==goal)//如果x的父结点的父结点是goal，旋转一次即可
        {
            pushdown(pre[x]);//机械臂翻转x的父结点
            pushdown(x);//机械臂翻转x自己
            Rotate(x,tree[pre[x]][0]==x);//旋转x
        }
        else
        {
            pushdown(pre[pre[x]]);//机械臂翻转x的父结点的父结点
            pushdown(pre[x]);//机械臂翻转x的父结点
            pushdown(x);//机械臂翻转x自己
            int y=pre[x];//y表示x的父结点
            int c=(tree[pre[y]][0]==y);//y是左儿子，c=1;y是右儿子，c=0
            if(tree[y][c]==x)//如果y是左儿子，y的右儿子是x;或者y是右儿子，y的左儿子是x（三点不共线）
            {
                Rotate(x,!c);//x是左儿子右旋（或x是右儿子左旋）
                Rotate(x,c);//然后再左旋（右旋）
            }
            else//如果y是左儿子，x是y的左儿子或者y是右儿子，x是y的右儿子（三点共线）
            {
                Rotate(y,c);//y旋转
                Rotate(x,c);//x旋转
            }
        }
    }
    pushup(x);//就是以x为根的子树包含多少个子结点
    if(goal==0)
        root=x;//goal为0，x旋转到根
}
int get_max(int x)//获得最大值
{
    pushdown(x);//机械臂翻转x
    while(tree[x][1])//x的右儿子存在
    {
        x=tree[x][1];//x变成x的右儿子
        pushdown(x);//继续机械臂翻转x
    }
    return x;
}
void del_root()//删除根结点（待删结点已经被旋转到根了）
{
    if(tree[root][0]==0)//如果根结点的左儿子不存在
    {
        root=tree[root][1];//直接删除根结点，右儿子变成新的根
        pre[root]=0;//右儿子的父结点变成0
    }
    else {//如果根结点的左儿子存在
        int m=get_max(tree[root][0]);//m为根结点的左子树的最大值
        splay(m,root);//把m旋转到根，左子树的最大值代替根
        tree[m][1]=tree[root][1];//m变成根结点，所以m的右儿子等于原根结点的右儿子
        pre[tree[root][1]]=m;//原根结点的右儿子的父结点变成m
        root=m;//根变成m
        pre[root]=0;//根m的父结点变成0
        pushup(root);//计算新根m的子树包含多少个子结点
    }
}
void newnode(int &x,int fa,int val)//增加一个新结点，已知新结点x，父结点fa，val为x所表示的编号的位置
{
    x=val;//给新结点x赋值
    pre[x]=fa;//建立x的父结点
    size[x]=1;//初始size值
    rev[x]=0;//x未被旋转
    tree[x][0]=tree[x][1]=0;//左右儿子不存在
}
void buildtree(int &x,int l,int r,int fa)//建树，知道新结点x，左儿子，右儿子，父结点
{
    if(l>r)//如果左儿子大于右儿子就退出
        return;
    int mid=(l+r)>>1;//求左右儿子的中间值mid
    newnode(x,fa,mid);//给树增加一个新结点x，知道父结点和自己的值
    buildtree(tree[x][0],l,mid-1,x);//建新结点x的左儿子
    buildtree(tree[x][1],mid+1,r,x);//建新结点的右儿子
    pushup(x);//计算以x为根的子树包含多少个子结点
}
void init(int n)//给1～n的序列建树
{
    root=0;//根等于0
    tree[root][0]=tree[root][1]=pre[root]=size[root]=0;//根的左右儿子及父结点、子结点个数都等于0
    buildtree(root,1,n,0);//从根开始建树
}
int main()
{
    int n;//个数
    while(~scanf("%d",&n)&&n)
    {
        init(n);//给n个数建树（建位置）
        for(int i=1; i<=n; i++)
        {
            scanf("%d",&nodes[i].val);//每个位置(结点）的val对应数(编号)
            nodes[i].id=i;//每个位置(结点)的id就是位置本身
        }
        sort(nodes+1,nodes+n+1);//给结点按照编号和编号对应的位置从小到大排序
        for(int i=1; i<n; i++)
        {
            splay(nodes[i].id,0);//第i次翻转，把第i大的数旋转到根
            update_rev(tree[root][0]);//根的左子树需要翻转
            printf("%d ",i+size[tree[root][0]]);//输出第i次翻转+第i个被翻转数的左边的个数，就是他左子树的个数
            del_root();//删除第i次翻转的数，准备下一次翻转
        }
        printf("%d\\n",n);
    }
    return 0;
}

---

好难，还没明白，明天画个图再继续_(:з」∠)_