二叉排序树的定义及基本操作（构造查找插入删除）递归及非递归算法

Posted 2021-08-30 薛定谔的猫ovo

文章目录

• • 二叉排序树的定义
  • 二叉排序树的查找
  • 二叉排序树的插入
  • 二叉排序树的构造
  • 二叉排序树的删除
  • 完整代码及实例
  • 二叉排序树的查找效率

二叉排序树的定义

二叉排序树（Binary Sort Tree， BST），也称二叉查找树。
二叉排序树或者是一棵空树，或者是一棵具有下列特性的非空二叉树：
1） 若左子树非空，则左子树上所有结点关键字均小于根结点的关键字值；
2） 若右子树非空，则右子树上所有结点关键字均大于根结点的关键字值；
3） 左、右子树本身也分别是一棵二叉排序树。

由定义可知，二叉排序树是一个递归的数据结构，可以方便的使用递归算法对二叉排序树进行各种运算。
根据二叉树的定义，可得左子树结点值 ＜ 根结点值 ＜ 右子树结点值。
所以，对二叉排序树进行中序遍历，可以得到一个递增的有序序列。

二叉排序树的结点定义：

typedef struct BSTNode{
    int data;
    struct BSTNode *left;
    struct BSTNode *right;
}BSTNode;

二叉树结点的创建：

//二叉树结点创建
BSTNode *CreateTreeNode(int x){
    BSTNode *p = (BSTNode *)malloc(sizeof(BSTNode));
    p->data = x;
    p->left = NULL;
    p->right = NULL;
    return p;
}

二叉排序树的查找

 二叉排序树的查找是从根结点开始的，沿某个分支逐层向下进行比较的过程。
 其查找过程描述如下：若二叉排序树非空，则将给定值与根结点的关键字比较，若相等，则查找成功；若不等，则当根结点的关键字值大于给定关键字值时，在根结点的左子树中查找；否则在根结点的右子树中查找。

实现代码：

//查找的递归算法
BSTNode *Search(BSTNode *root, int x){
    if(root->data == x){
        return root;
    }else if(x < root->data){
        return Search(root->left, x);
    }else{
        return Search(root->right, x);
    }
}

//查找的非递归算法
BSTNode *Search(BSTNode *root, int x){
    BSTNode *p = root;
    while(p!=NULL && p->data!=x){
        if(x < p->data)
            p = p->left;
        else
            p = p->right;
    }
    return p;
}

二叉排序树的插入

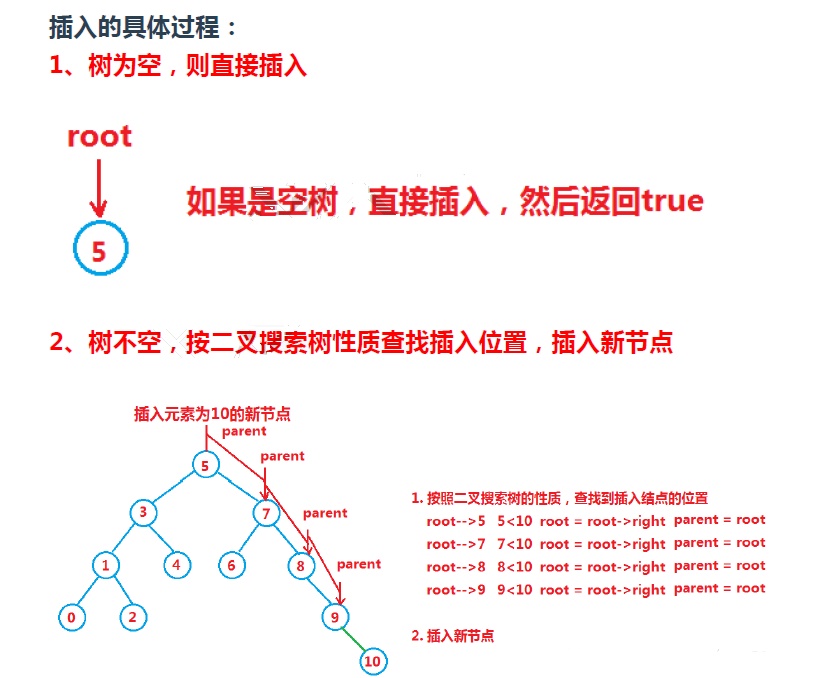
 二叉排序树作为一种动态集合，其特点是树的结构通常不是一次生成的，而是在查找过程中，当树中不存在关键字等于给定值的结点时再进行插入的。
 由于二叉排序树是递归定义的，因此插入结点的过程如下：若原二叉排序树为空，则直接插入结点；否则，若关键字＜根结点关键字，则插入左子树，若关键字＞根结点关键字，则插入右子树。

实现代码：

//插入的递归算法
BSTNode *Insert(BSTNode *root, int x){
    if(root == NULL){
        root = CreateTreeNode(x);
        return root;
    }
    if(x < root->data){
        root->left = Insert(root->left, x);
    }
    if(x > root->data){
        root->right = Insert(root->right, x);
    }
    return root;
}

//插入的非递归算法
BSTNode *Insert1(BSTNode *root, int x){
    BSTNode *parent = NULL;
    BSTNode *p = root;
    if(root == NULL){
        root = CreateTreeNode(x);
        return root;
    }
    while(p != NULL){
        parent = p;
        if(x < p->data){
            p = p->left;
        }else{
            p = p->right;
        }
    }
    if(parent->data >x){
        parent->left = CreateTreeNode(x);
    }else{
        parent->right = CreateTreeNode(x);
    }
    return root;
}

二叉排序树的构造

 构造一棵二叉排序树就是依次输入数据元素，并将它们插入二叉排序树中适当位置上的过程。
 构造二叉排序树的过程：每读入一个元素，就建立一个新结点，若二叉排序树为空，则将新结点作为二叉排序树的根结点；若二叉排序树非空，则将新结点的值与根结点的值比较，若小于根结点的值，则插入左子树，否则插入右子树。

实现代码：

void Create(BSTNode *&root, int str[], int n){
    root = NULL;
    for(int i=0; i<n; i++){
        Insert(root, str[i]);
    }
}

二叉排序树的删除

 在二叉排序树中删除一个结点时，不能把以该结点为根的子树上的结点都删除，必须先把被删除结点从存储二叉排序树的链表上摘下来，将因删除结点而断开的二叉链表重新链接起来，同时**确保二叉排序树的性质（左子树结点值＜根结点值＜右子树结点值）**不会丢失。

 删除操作一般会出现三种情况：
1） 若被删除结点z是叶结点，则直接删除，不会破坏二叉排序树的性质。
2） 若结点z只有一棵左子树或右子树，则让z的子树成为z父结点的子树，替代z的位置。
3） 若结点z有左、右两棵子树，则令z的直接后继（或直接前驱）替代z，然后从二叉排序树中删除这个直接后继（或直接前驱），这样就转换成了第一或第二种情况。

 注：已知二叉排序树经过中序遍历可以得到一个递增的有序序列，这里的直接后继（或直接前驱）应该是指被删除结点在这个中序遍历序列中的直接后继（或直接前驱）。
 
 体现在二叉排序树的图中:
 某个结点的直接后继为以该结点为根的右子树中最左下位置的结点，即右子树的最小值；
 某个结点的直接前驱为以该结点为根的左子树中最右下位置的结点，即左子树的最大值。

下面依次给出以上三种情况的实例及删除操作：
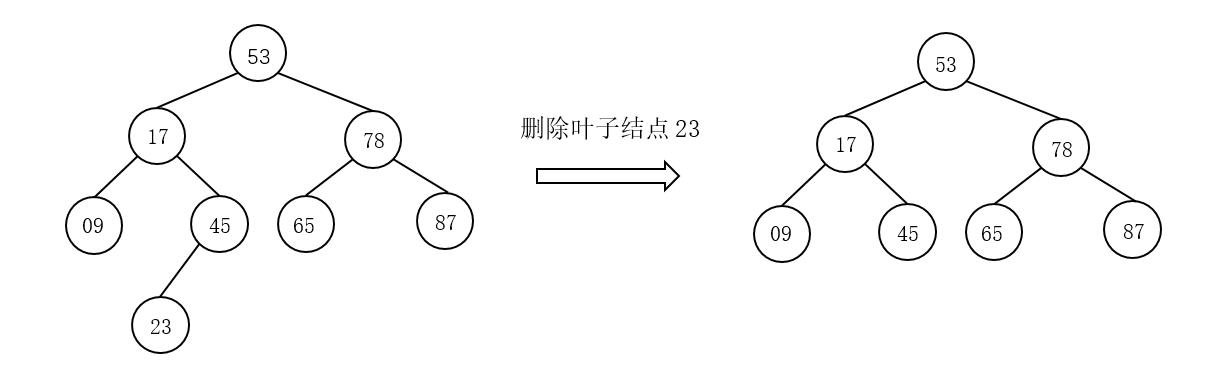
<1> 被删除结点是叶结点，如删除关键字为23的叶子结点。

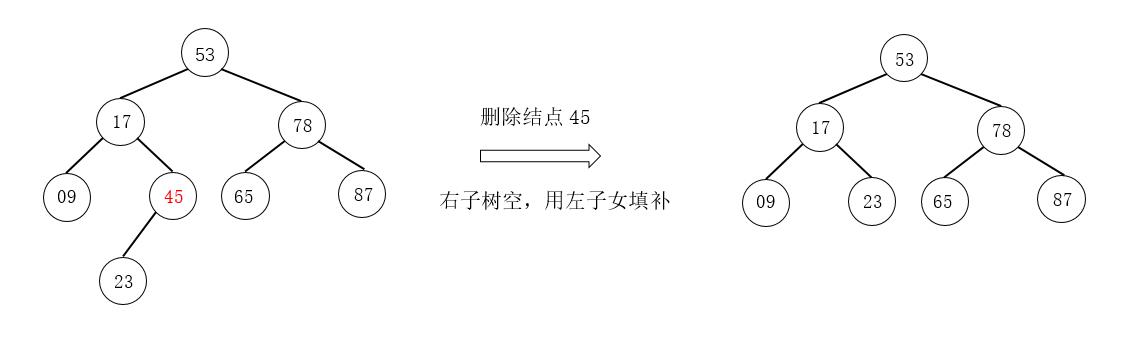
<2.1>被删除结点z只有一棵左子树，删除关键字为45的结点。

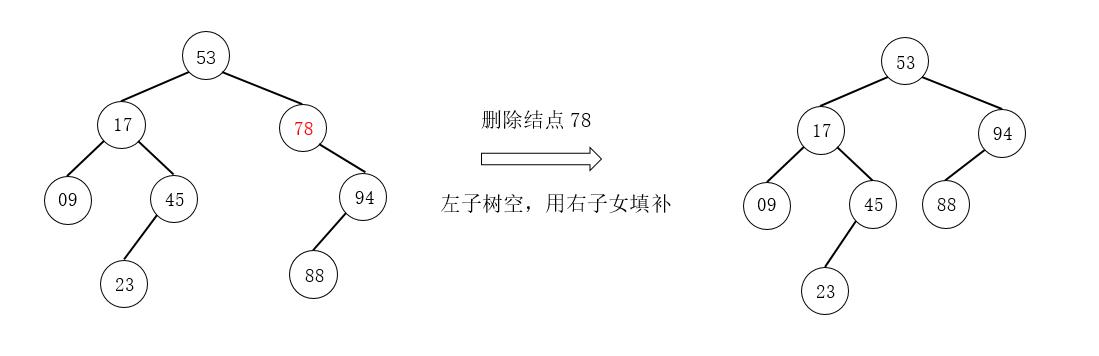
<2.2>被删除结点z只有一棵右子树，如删除关键字为78的结点。

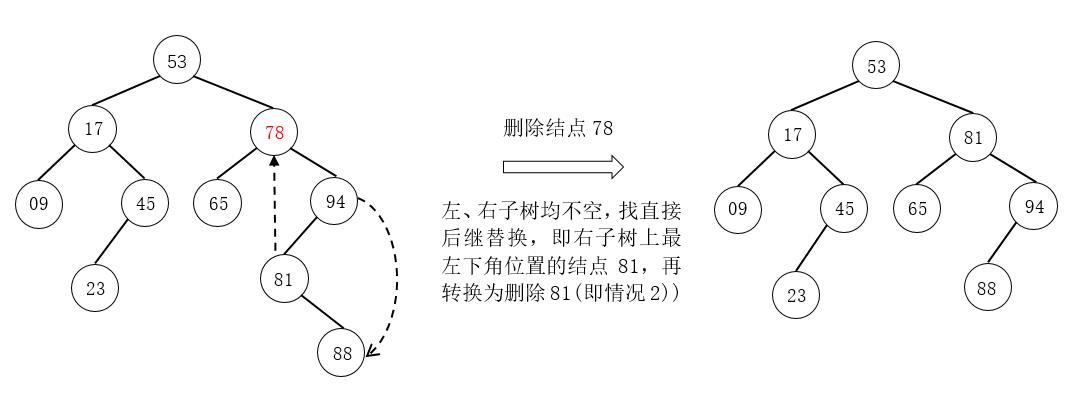
<3>被删除结点z有左、右两棵子树，如删除结点78。
 再强调一下寻找替代被删除结点的结点的原则以供结合下图思考：

 已知二叉排序树经过中序遍历可以得到一个递增的有序序列，这里的直接后继（或直接前驱）应该是指被删除结点在这个中序遍历序列中的直接后继（或直接前驱）。
 
 体现在二叉排序树的图中:
 某个结点的直接后继为以该结点为根的右子树中最左下位置的结点，即右子树的最小值；
 某个结点的直接前驱为以该结点为根的左子树中最右下位置的结点，即左子树的最大值。

实现代码：

//删除
bool Delete(BSTNode *p){
    //在二叉排序树中删除结点p, 并重新连接它的左右子树
    BSTNode *q, *s;
    //1.p为叶子结点
    if(p->left==NULL && p->right==NULL){
        p = NULL;
    }
    //2.1 p左子树为空, 重接右子树
    else if(p->left == NULL){
        q = p;
        p = p->right;
        free(q);
    }
    //2.2 p右子树为空, 重接左子树
    else if(p->right == NULL){
        q = p;
        p = p->left;
        free(q);
    }
    //3. p左右子树均不为空
    else{
        q = p;
        s = p->right; //找到p的右子树的最左端（中序直接后继）
        while(s->left != NULL){
            q = s;
            s = s->left;
        }
        p->data = s->data;
        
        if(q != p) //判断是否执行上述while循环
            q->left = s->right; //执行上述while循环，重接*q的左子树
        else
            q->right = s->right; //未执行上述while循环，重接*q的右子树
        free(s);
    }
    return true;
}
bool DeleteBST(BSTNode *root, int x){
    if(root == NULL){
        return false;
    }else{
        if(x == root->data)
            return Delete(root); 
        else if(x < root->data)
            return DeleteBST(root->left, x);
        else
            return DeleteBST(root->right, x);
    }
}

上面的代码中，在情况3中选择的是用被删除结点z的直接后继替代z，当然也可以用被删除结点z的直接前驱来替代，那么则需要修改为如下的代码即可。

//3. p左右子树均不为空
    else{
        q = p;
        s = p->left; //找到p的左子树的最右端（中序直接前驱）
        while(s->right != NULL){
            q = s;
            s = s->right;
        }
        p->data = s->data;
        
        if(q != p) //判断是否执行上述while循环
            q->right = s->left; //执行上述while循环，重接*q的右子树
        else
            q->left = s->left; //未执行上述while循环，重接*q的左子树
        free(s);
    }

完整代码及实例

#include<bits/stdc++.h>
using namespace std;

typedef struct BSTNode{
    int data;
    struct BSTNode *left;
    struct BSTNode *right;
}BSTNode;

#define N 100 

//查找的递归算法
BSTNode *Search(BSTNode *root, int x){
    if(root->data == x){
        return root;
    }else if(x < root->data){
        return Search(root->left, x);
    }else{
        return Search(root->right, x);
    }
}
//查找的非递归算法
BSTNode *Search1(BSTNode *root, int x){
    BSTNode *p = root;
    while(p!=NULL && p->data!=x){
        if(x < p->data)
            p = p->left;
        else
            p = p->right;
    }
    return p;
}

//二叉树结点创建
BSTNode *CreateTreeNode(int x){
    BSTNode *p = (BSTNode *)malloc(sizeof(BSTNode));
    p->data = x;
    p->left = NULL;
    p->right = NULL;
    return p;
}

//插入的递归算法
BSTNode *Insert(BSTNode *root, int x){
    if(root == NULL){
        root = CreateTreeNode(x);
        return root;
    }
    if(x < root->data){
        root->left = Insert(root->left, x);
    }
    if(x > root->data){
        root->right = Insert(root->right, x);
    }
    return root;
}
//插入的非递归算法
BSTNode *Insert1(BSTNode *root, int x){
    BSTNode *parent = NULL; //记录当前结点的父结点
    BSTNode *p = root;
    if(root == NULL){
        root = CreateTreeNode(x);
        return root;
    }
    while(p != NULL){
        parent = p;
        if(x < p->data){
            p = p->left;
        }else{
            p = p->right;
        }
    }
    if(parent->data >x){
        parent->left = CreateTreeNode(x);
    }else if(parent->data < x){
        parent->right = CreateTreeNode(x);
    }
    return root;
}


//构建
void Create(BSTNode *&root, int str[], int n){
    root = NULL;
    for(int i=0; i<n; i++){
        root = Insert(root, str[i]);
    }
}

//删除
bool Delete(BSTNode *p){
    //在二叉排序树中删除结点p, 并重新连接它的左右子树
    BSTNode *q, *s;
    //1.p为叶子结点
    if(p->left==NULL && p->right==NULL){
        p = NULL;
    }
    //2.1 p左子树为空, 重接右子树
    else if(p->left == NULL){
        q = p;
        p = p->right;
        free(q);
    }
    //2.2 p右子树为空, 重接左子树
    else if(p->right == NULL){
        q = p;
        p = p->left;
        free(q);
    }
    //3. p左右子树均不为空
    else{
        q = p;
        s = p->right; //找到p的右子树的最左端（中序直接后继）
        while(s->left != NULL){
            q = s;
            s = s->left;
        }
        p->data = s->data;
        
        if(q != p) //判断是否执行上述while循环
            q->left = s->right; //执行上述while循环，重接*q的左子树
        else
            q->right = s->right; //未执行上述while循环，重接*q的右子树
        free(s);
    }
    return true;
}
bool DeleteBST(BSTNode *root, int x){
    if(root == NULL){
        return false;
    }else{
        if(x == root->data)
            return Delete(root); 
        else if(x < root->data)
            return DeleteBST(root->left, x);
        else
            return DeleteBST(root->right, x);
    }
}


void LevelOrder(BSTNode *root){
    queue<BSTNode *> treenode; //队列存储结点
    if(root != NULL)
        treenode.push(root); //根结点入队
    while(!treenode.empty()){
        BSTNode *p = treenode.front(); 
        treenode.pop(); //根结点出队
        cout<<p->data<<" "; //输出队首元素，即当前访问的结点值
        if(p->left != NULL){
            treenode.push(p->left);//如果有左子树，则将左子树的根结点入队
        }
        if(p->right != NULL){
            treenode.push(p->right);//如果有右子树，则将右子树的根结点入队
        }
    }
}

int main(){
    BSTNode *root;
    int n;
    cin>>n;
    int str[n];
    for(int i=0; i<n; i++){
        cin>>str[i];
    }
    Create(root,str,n); 
    cout<<"当前二叉排序树的层序遍历序列为：";
    LevelOrder(root);
    cout<<endl;
    BSTNode *p = Search(root, 17);
    cout<<"结点17的右孩子结点值为："<<p->right->data<<endl;
    DeleteBST(root, 78);
    cout<<"删除结点78后的二叉排序树的层序遍历序列为：";
    LevelOrder(root);
    return 0;
}

构建的二叉排序树如下图所示，删除时为删除结点78.

运行结果为：

二叉排序树的查找效率

二叉排序树查找算法的平均查找长度，主要取决于树的高度，即与二叉树的形态有关。

---

查找成功的平均查找长度为：  Σ(本层高度*本层结点个数) / 结点总数
查找不成功的平均查找长度为：   Σ(本层高度*本层补上的叶子结点个数) / 补上的叶子总数

---

如图所示的二叉排序树：

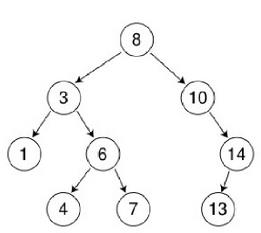
查找成功的平均查找长度为：（11 + 22 + 33 + 43）/ 9

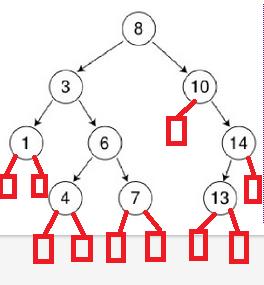
查找不成功的平均查找长度：（21 + 33 + 4*6）/ 10