Codeforces1555 E. Boring Segments（尺取+线段树）

Posted 2021-08-30 live4m

题意：

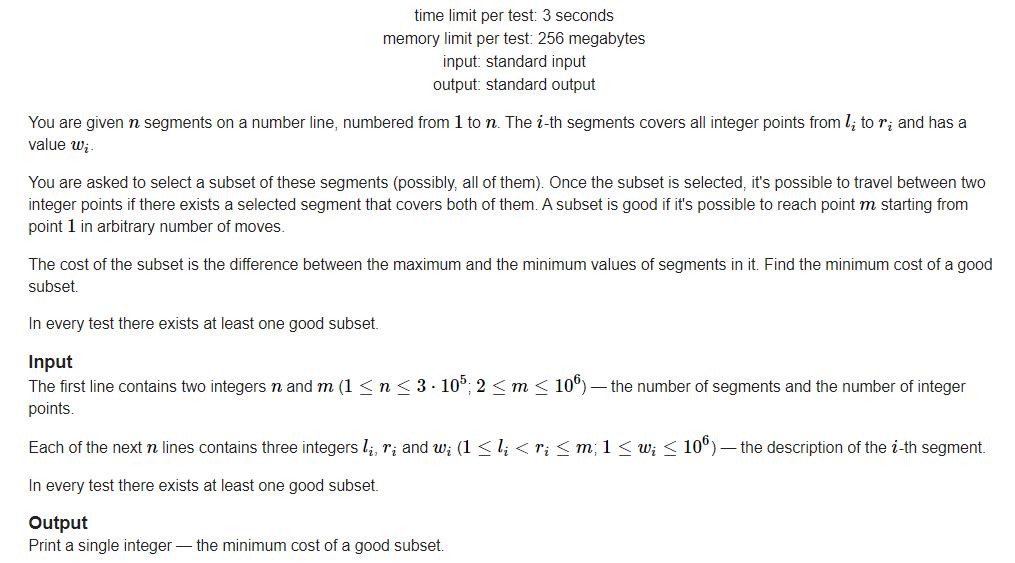
解法：

将线段按照w从小到大排序.

然后从左到右枚举线段r,
尺取维护一个最大的l,满足[l,r]能够覆盖[1,m],
判断[l,r]中的线段能否覆盖[1,m],可以用线段树区间加法,
维护每个点被覆盖的次数,同时维护区间最小值,
如果最小值>0,说明全覆盖了.

对于满足条件的区间,用w的差值更新答案即可.

算法总复杂度O(n*log)

ps:
这题其实说的不是区间覆盖,而是能够连通,
例如[1,3]和[4,5]是不连通的,因为线段之间没有相交
而[1,3]和[3,5]是连通的.
处理方法是将m--,每条线段的右端点r--,
这样的话就不需要判相交,只需要判断是否覆盖了[1,m]就行了.

code：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxm=2e6+5;
struct Node{
    int l,r,w;
}e[maxm];
bool cmp(Node a,Node b){
    return a.w<b.w;
}
struct Tree{
    int mi[maxm<<2];
    int laz[maxm<<2];
    void pp(int node){
        mi[node]=min(mi[node*2],mi[node*2+1]);
    }
    void pd(int node){
        if(laz[node]){
            mi[node*2]+=laz[node];
            mi[node*2+1]+=laz[node];
            laz[node*2]+=laz[node];
            laz[node*2+1]+=laz[node];
            laz[node]=0;
        }
    }
    void update(int st,int ed,int val,int l,int r,int node){
        if(st<=l&&ed>=r){
            laz[node]+=val;
            mi[node]+=val;
            return ;
        }
        pd(node);
        int mid=(l+r)/2;
        if(st<=mid)update(st,ed,val,l,mid,node*2);
        if(ed>mid)update(st,ed,val,mid+1,r,node*2+1);
        pp(node);
    }
}T;
int n,m;
void solve(){
    cin>>n>>m;
    m--;
    for(int i=1;i<=n;i++){
        int l,r,w;cin>>l>>r>>w;
        r--;
        e[i]={l,r,w};
    }
    sort(e+1,e+1+n,cmp);
    int ans=1e18;
    int l=1;
    for(int i=1;i<=n;i++){
        T.update(e[i].l,e[i].r,1,1,m,1);
        while(T.mi[1]>0){
            ans=min(ans,e[i].w-e[l].w);
            T.update(e[l].l,e[l].r,-1,1,m,1);
            l++;
        }
    }
    cout<<ans<<endl;
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);
    solve();
    return 0;
}

---