收藏第一课第二周作业-学会计算分类各种指标-超详细教程

Posted 2021-08-30 Tina姐

本次作业文件：
在第一课/第一课大作业/week2metric

这节课不需要对模型进行预测，所有的预测结果已经在csv文件中给出。

作为提醒，我们的数据集包含14种不同情况的X射线，可通过X射线诊断。我们将使用我们在这一周中学习的分类指标来评估我们模型的表现。

作业目录

1. Packages
2. Overview
3. Metrics
   3.1 True Positives, False Positives, True Negatives, and False Negatives
   3.2 Accuracy
   3.3 Prevalence
   3.4 Sensitivity and Specificity
   3.5 PPV and NPV
   3.6 ROC Curve
4. Confidence Intervals 置信区间
5. Precision-Recall Curve
6. F1 Score
7. Calibration(校准)

注意： 在作业文件中，可以直接跳转到你感兴趣的章节。

你将学会一下内容：

1. Accuracy
2. Prevalence
3. Specificity & Sensitivity
4. PPV and NPV
5. ROC curve and AUCROC (c-statistic)
6. Confidence Intervals

1.3 从csv获得预测结果和真实标签

预测结果和真实标签存储在两个名为train_preds.CSV和valid_preds.CSV的CSV文件中。

train_results = pd.read_csv("train_preds.csv")
valid_results = pd.read_csv("valid_preds.csv")

可以查看一下csv文件的信息，使用 valid_results.info()

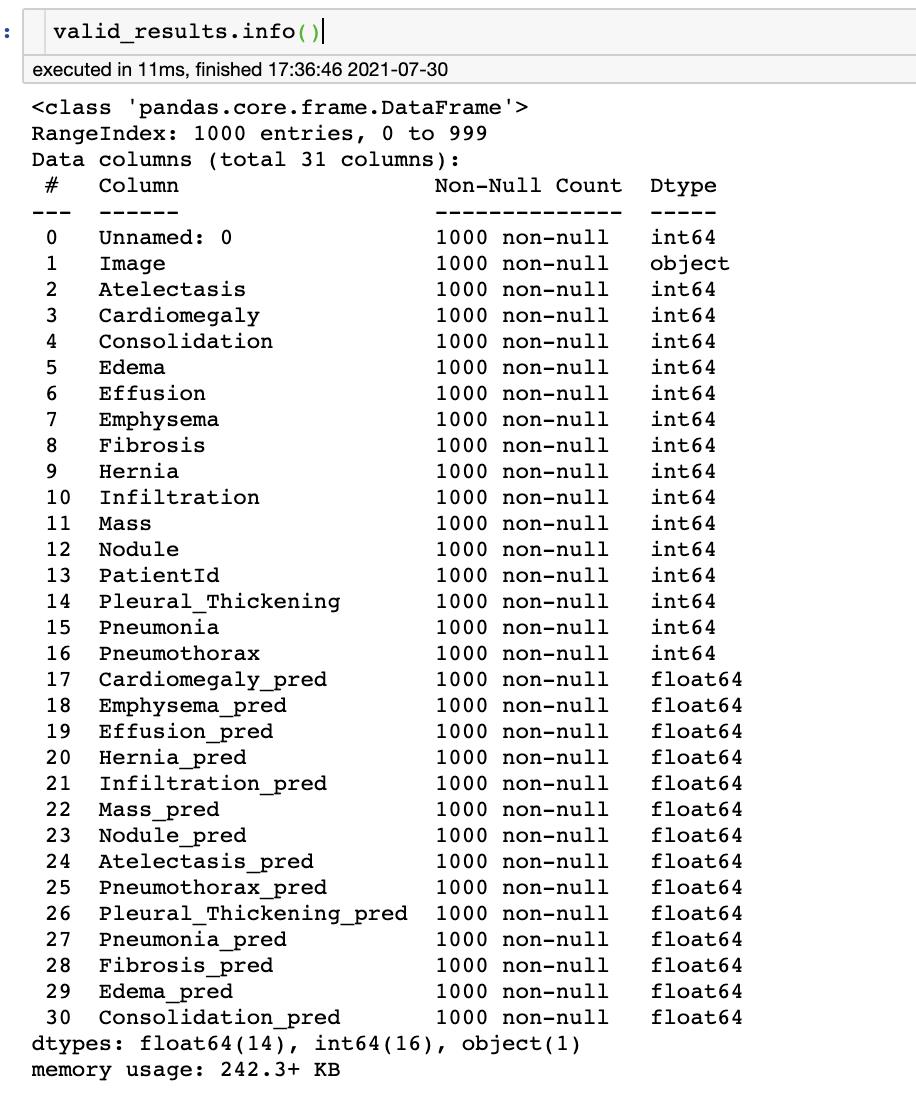
可以看到 该 csv 有 1000 行 31 列，以及每一列的名字和数据类型。

如 2-16列一共是14种疾病的真实标签值，17-30列是对应的预测值

因此，我们就可以获得这些示例的 标签 y 和 预测值 pred

y = valid_results[class_labels].values
pred = valid_results[pred_labels].values

1.4.1 真阳性、假阳性、真阴性和假阴性

从模型预测计算的最基本的统计数据是真阳性、真阴性、假阳性和假阴性。

顾名思义

真阳性（TP）：模型将示例分类为阳性，实际标签也为阳性。
假阳性 (FP)：模型将示例分类为正例，但实际标签为负例。
真阴性（TN）：模型将示例分类为负，实际标签也为负。
假阴性（FN）：模型将示例分类为阴性，但标签实际上是阳性。

我们将计算给定数据中 TP、FP、TN 和 FN 的数量。我们所有的指标都可以建立在这四个统计数据之上。

回想一下，该模型输出 0-1 之间的实数。我们需要将它们转换为 0 或 1。我们将使用阈值 $th$ 来做到这一点.

• 模型的输出结果 > $th$， 则 预测结果 pred = 1
• 模型的输出结果 < $th$， 则 预测结果 pred = 0

我们所有的指标（最后的 AUC 除外）都将取决于此阈值的选择，阈值默认为0.5。

使用下面的函数分别计算 TP、FP、TN 和 FN

def true_positives(y, pred, th=0.5):
    TP = 0   
    # get thresholded predictions
    thresholded_preds = pred >= th
    # compute TP
    TP = np.sum((y == 1) & (thresholded_preds == 1))
    return TP
def true_negatives(y, pred, th=0.5):
    TN = 0  
    # get thresholded predictions
    thresholded_preds = pred >= th
    # compute TN
    TN = np.sum((y == 0) & (thresholded_preds == 0)) 
    return TN
def false_positives(y, pred, th=0.5):
    FP = 0    
    # get thresholded predictions
    thresholded_preds = pred >= th
    # compute FP
    FP = np.sum((y == 0) & (thresholded_preds == 1))   
    return FP
def false_negatives(y, pred, th=0.5):
    FN = 0
    # get thresholded predictions
    thresholded_preds = pred >= th  
    # compute FN
    FN = np.sum((y == 1) & (thresholded_preds == 0))
    return FN

通过如下图可直观理解 TP、FP、TN 和 FN

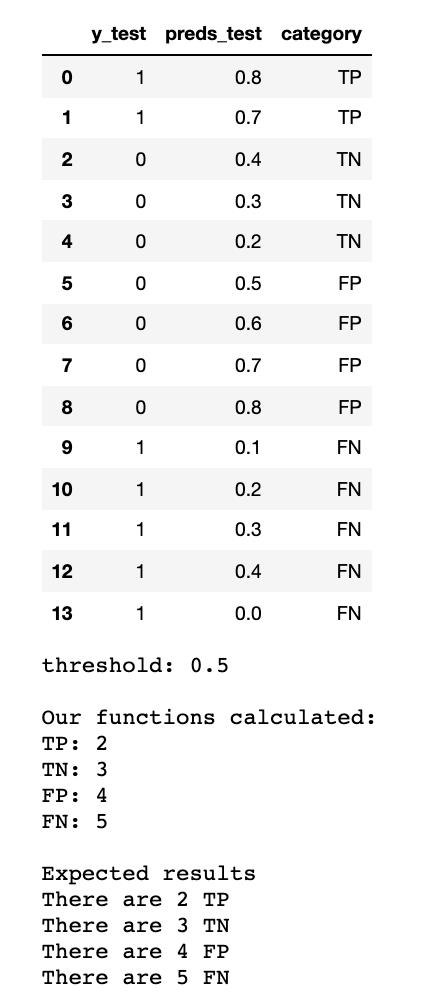
比如图上第一个值，preds_test=0.8 > 阈值0.5,则预测值为1。y_test=1，说明为TP。

接下来为每个类计算 TP、FP、TN 和 FN。在 utils.py 中已经给出功能函数。直接调用即可

util.get_performance_metrics(y, pred, class_labels)

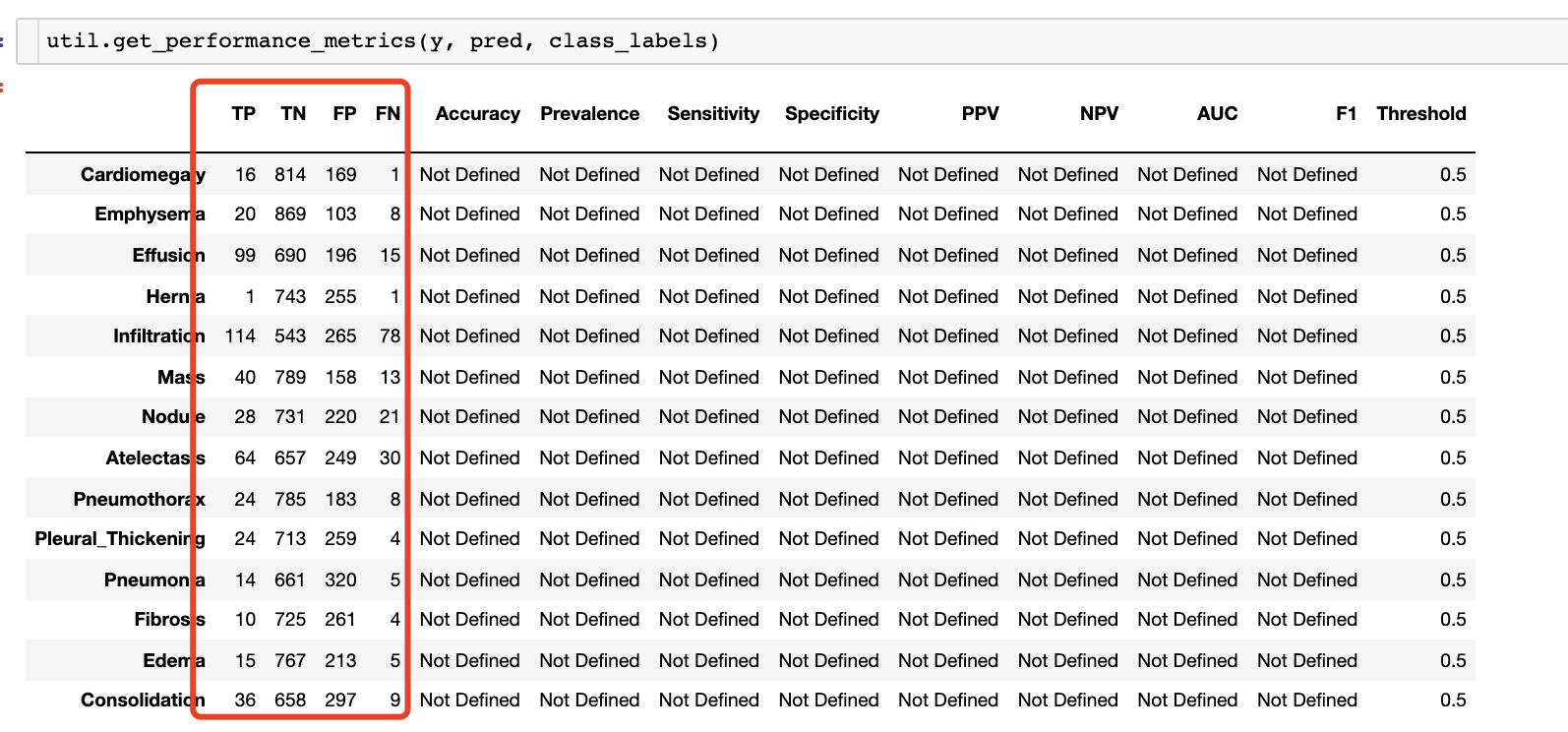
1.4.2 计算 Accuracy

使用 TP、FP、TN 和 FN来表示 accuracy
$$accuracy=\frac{\text{true positives}+\text{true negatives}}{\text{true positives}+\text{true negatives}+\text{false positives}+\text{false negatives}}$$
用代码表示为

def get_accuracy(y, pred, th=0.5):
    TP = true_positives(y,pred,th)
    FP = false_positives(y,pred,th)
    TN = true_negatives(y,pred,th)
    FN = false_negatives(y,pred,th)
    # Compute accuracy using TP, FP, TN, FN
    accuracy = (TP + TN) / (TP + TN + FP + FN)  
    return accuracy

1.4.3 Prevalence 患病率

另一个重要的概念是患病率（流行度）

1. 在医学背景下，患病率是人口中患有疾病（或病症等）的人的比例。
2. 在机器学习术语中，这是阳性的比例。流行度的表达式为：
   $$prevalence=\frac{1}{N}\sum _i{y}_i$$
   N：样本总数

def get_prevalence(y):
    prevalence = 0.0
    prevalence = np.mean(y)
    return prevalence

举例测试一下

# Test
y_test = np.array([1, 0, 0, 1, 1, 0, 0, 0, 0, 1])
print(f"computed prevalence: {get_prevalence(y_test)}")

computed prevalence: $4/10=0.4$

1.4.4 Sensitivity and Specificity

敏感性和特异性是用于衡量分类的两个最重要的指标。

• 敏感性是判断如果案例实际是阳性，我们预测为阳性的概率。
• 特异性是给定病例实际上是阴性的情况下模型输出阴性的概率。
  $$sensitivity=\frac{\text{true positives}}{\text{true positives}+\text{false negatives}}$$

$$specificity=\frac{\text{true negatives}}{\text{true negatives}+\text{false positives}}$$

def get_sensitivity(y, pred, th=0.5):
    TP = true_positives(y,pred,th)
    FN = false_negatives(y,pred,th)
    # use TP and FN to compute sensitivity
    sensitivity = TP/(TP+FN)
    return sensitivity

def get_specificity(y, pred, th=0.5):
    TN = true_negatives(y,pred,th)
    FP = false_positives(y,pred,th) 
    # use TN and FP to compute specificity 
    specificity = TN/(TN+FP)
 return specificity

1.4.5 PPV and NPV

然而在诊断上，敏感性和特异性没有帮助。

例如，敏感性告诉我们，假设该人已经患有这种疾病，我们的测试输出阳性的概率。但是，我们实际中，事先并不知道患者是否是阳性。

如果我们的测试结果为阳性，那有多大的概率这个病人确实是阳性呢。这就要用阳性预测值 (PPV) 和阴性预测值 (NPV)。

• 阳性预测值 (PPV) 是筛查试验阳性的受试者确实患有该疾病的概率。
• 阴性预测值 (NPV) 是筛查试验阴性的受试者确实没有患病的概率。

$$PPV=\frac{\text{true positives}}{\text{true positives}+\text{false positives}}$$

$$NPV=\frac{\text{true negatives}}{\text{true negatives}+\text{false negatives}}$$

def get_ppv(y, pred, th=0.5):
    TP = true_positives(y,pred,th)
    FP = false_positives(y,pred,th)
    # use TP and FP to compute PPV
    PPV =  TP/(TP+FP) 
    return PPV

def get_npv(y, pred, th=0.5):
    TN = true_negatives(y,pred,th)
    FN = false_negatives(y,pred,th)
    # use TN and FN to compute NPV
    NPV = TN/(TN+FN)
    return NPV

1.4.6 ROC Curve and AUC

到目前为止，我们一直在假设我们的模型对0.5及以上的预测应该被视为阳性，否则应该被视为阴性。

然而，这是一个相当随意的选择。

接收者操作特征 (ROC) 曲线是通过在各种阈值设置下绘制真阳性率 (TPR) 与假阳性率 (FPR) 来创建的。

理想点在左上角，真阳性率为1，假阳性率为0。曲线上的各个点都是通过逐渐改变阈值产生的。

通过代码调用

util.get_curve(y, pred, class_labels)

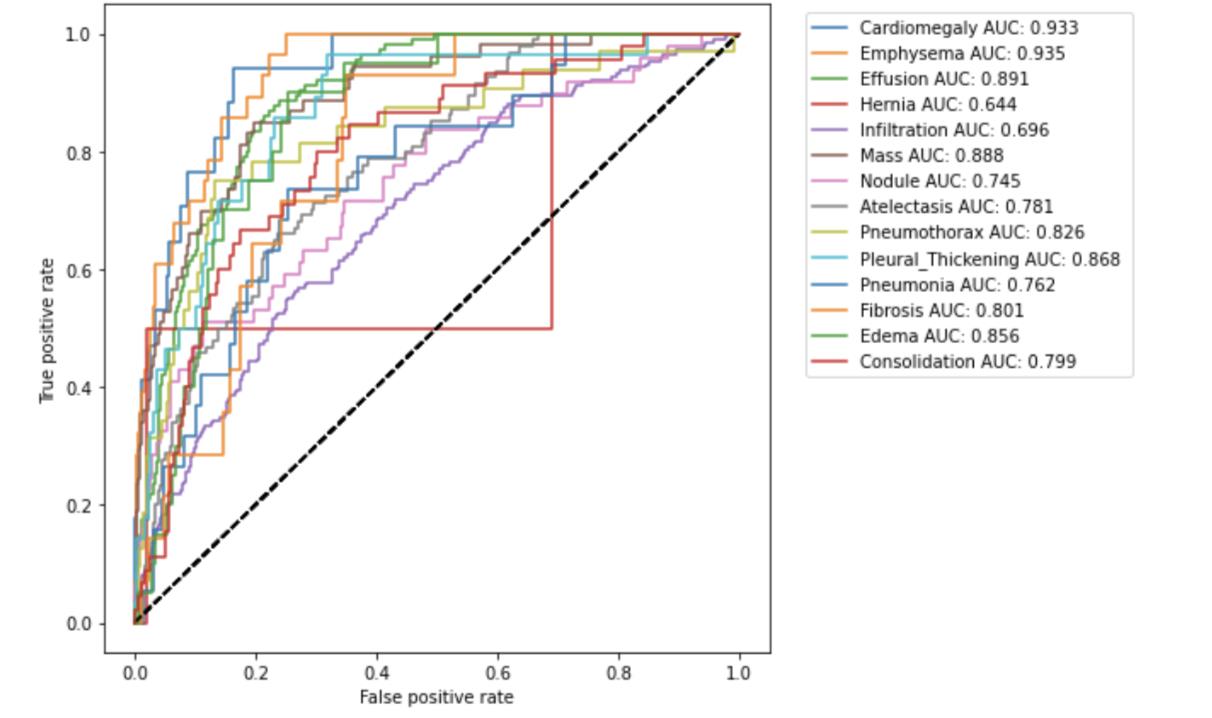
ROC 曲线下的面积也称为 AUROC 或 C 统计量，是拟合优度的度量。

让我们使用sklearn度量函数roc_auc_score计算AUC。

from sklearn.metrics import roc_auc_score
auc = roc_auc_score(y[:, 0], pred[:, 0])

计算第一个疾病的 $AUC=0.933$

如果作业代码以上都顺利跑通的话，可以得到如下列表

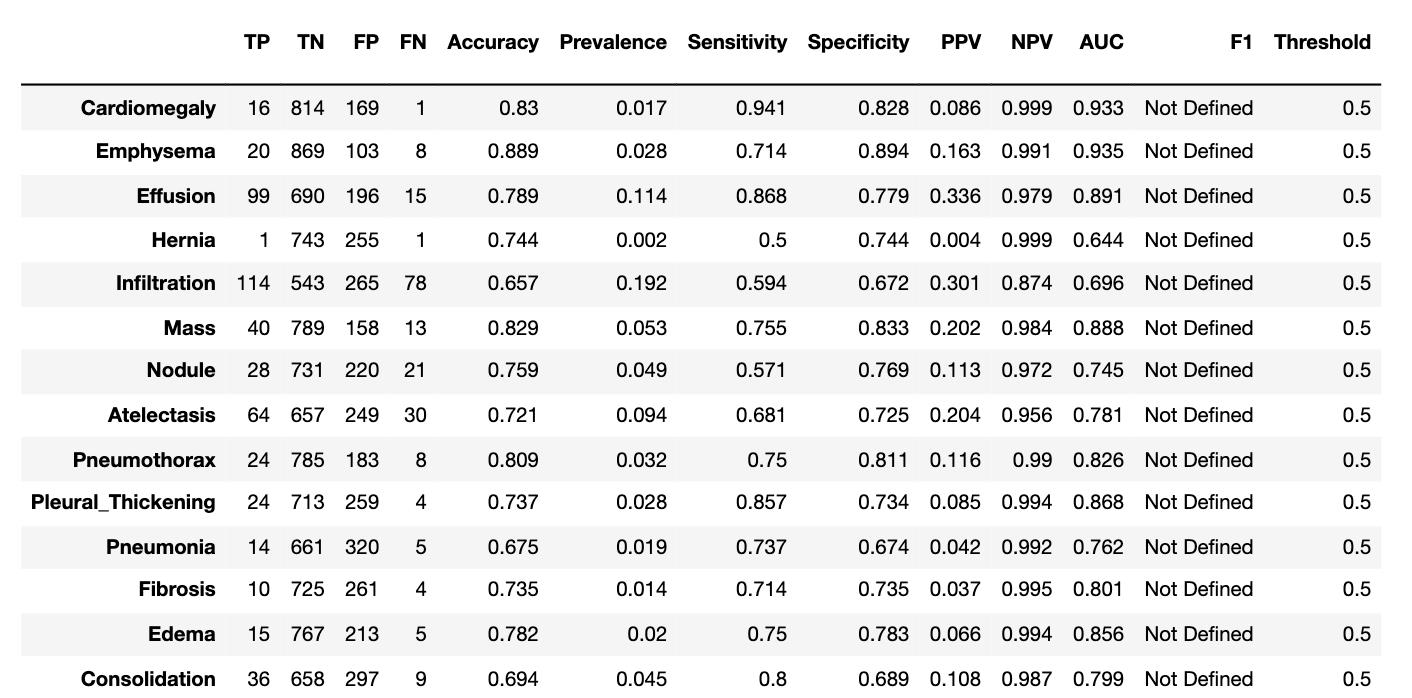
1.5 置信区间

置信区间在之前的解说中，已经讲过它的含义，可以翻看之前的文章。

吴恩达-第一课第二周8-10节-什么是置信区间，有什么作用

代码文件中也给出了相对正规的定义。这里，我使用大白话来做一个说明。

假设我们要求每个疾病的平均AUC, 以及估计它的总体样本的AUC 置信区间范围。用式子表述疾病 心脏增大（Cardiomegaly） 的均值和置信区间(CI 5%-95%) = $0.93(0.90-0.96)$

我们需要做如下几步

1. 做分层采样 n 次：

我们从数据集中（这里我们一直使用的是验证集）采样 1000 个样本，根据流行率来采样正负样本。一共采样 100次。

并且计算每次采样的样本的 mean auc, 存储在 statistics变量里， 因此，statistics的大小为 [classes, 100].

def bootstrap_auc(y, pred, classes, bootstraps = 100, fold_size = 1000):
    statistics = np.zeros((len(classes), bootstraps))

    for c in range(len(classes)):
        df = pd.DataFrame(columns=['y', 'pred'])
        df.loc[:, 'y'] = y[:, c]
        df.loc[:, 'pred'] = pred[:, c]
        # get positive examples for stratified sampling
        df_pos = df[df.y == 1]
        df_neg = df[df.y == 0]
        prevalence = len(df_pos) / len(df)
        for i in range(bootstraps):
            # stratified sampling of positive and negative examples
            pos_sample = df_pos.sample(n = int(fold_size * prevalence), replace=True)
            neg_sample = df_neg.sample(n = int(fold_size * (1-prevalence)), replace=True)

            y_sample = np.concatenate([pos_sample.y.values, neg_sample.y.values])
            pred_sample = np.concatenate([pos_sample.pred.values, neg_sample.pred.values])
            score = roc_auc_score(y_sample, pred_sample)
            statistics[c][i] = score
    return statistics

statistics = bootstrap_auc(y, pred, class_labels)

比如，第一个疾病的100次 AUC 为

2. 根据 statistics 计算每个类别的均值和置信区间

• 均值：就是求这100次的平均值
• 置信区间 假设我们要求的置信区间范围是 5%-95%
  可以使用函数 np.quantile()

def print_confidence_intervals(class_labels, statistics):
    df = pd.DataFrame(columns=["Mean AUC (CI 5%-95%)"])
    for i in range(len(class_labels)):
        mean = statistics.mean(axis=1)[i]
        max_ = np.quantile(statistics, .95, axis=1)[i]
        min_ = np.quantile(statistics, .05, axis=1)[i]
        df.loc[class_labels[i]] = ["%.2f (%.2f-%.2f)" % (mean, min_, max_)]
    return df

print_confidence_intervals这个函数在 utils.py里

所有疾病的 AUC 结果如下

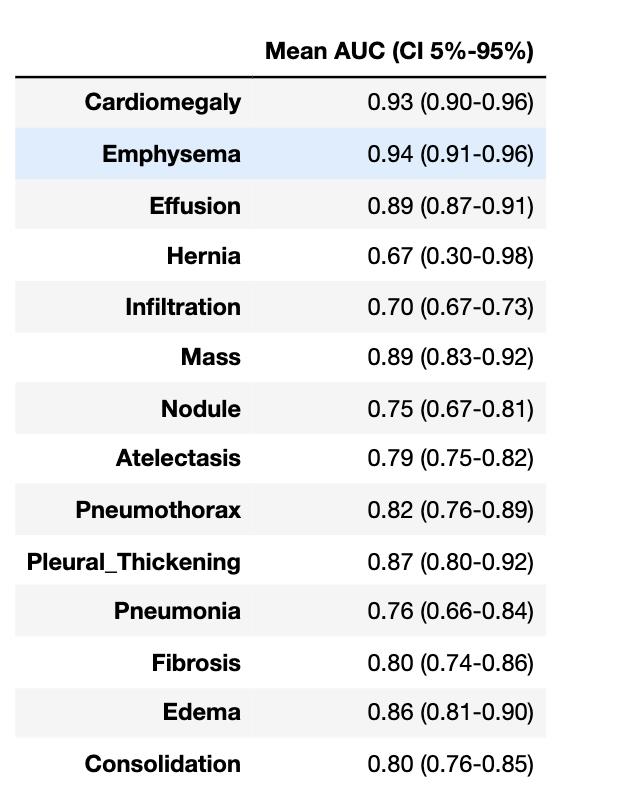
从表中可以看到，有些类别的置信区间很宽。

例如，疝气（Hernia)区间为 0.30-0.98，这表明我们不能确定它比偶然（0.5）好。

置信区间越大，越代表模型对其预测的不确定性

1.6 Precision-Recall Curve

当类别非常不平衡时，Precision-Recall（精确度-召回率） 是衡量预测成功与否的有用指标。

在信息检索中

• 精度是衡量结果相关性的指标，相当于我们之前定义的 PPV。
• 召回率衡量返回了多少真正相关的结果，这相当于我们之前定义的敏感度。

精确率-召回率曲线 (PRC) 显示了不同阈值下精确率和召回率之间的权衡。

曲线下方的高面积代表高召回率和高精度，其中高精度与低假阳性率相关，高召回率与低假阴性率相关。

两者的高分表明分类器正在返回准确的结果（高精度），以及返回大部分阳性结果（高召回率）。

PRC 可用 sklearn.metrics.precision_recall_curve 求得

def get_curve(gt, pred, target_names, curve='roc'):
    for i in range(len(target_names)):
        if curve == 'roc':
            curve_function = roc_curve
            auc_roc = roc_auc_score(gt[:, i], pred[:, i])
            label = target_names[i] + " AUC: %.3f " % auc_roc
            xlabel = "False positive rate"
            ylabel = "True positive rate"
            a, b, _ = curve_function(gt[:, i], pred[:, i])
            plt.figure(1, figsize=(7, 7))
            plt.plot([0, 1], [0, 1], 'k--')
            plt.plot(a, b, label=label)
            plt.xlabel(xlabel)
            plt.ylabel(ylabel)

            plt.legend(loc='upper center', bbox_to_anchor=(1.3, 1),
                       fancybox=True, ncol=1)
        elif curve == 'prc':
            precision, recall, _ = precision_recall_curve(gt[:, i], pred[:, i])
            average_precision = average_precision_score(gt[:, i]第一课第一周大作业-胸部14种疾病分类-代码详解

 吴恩达-医学图像人工智能专项课程-第一课第一周6-10节总结+作业解读
 吴恩达-第一课第二周8-10节-什么是置信区间，有什么作用
 第一课第三周大作业-- MRI 脑肿瘤自动分割教程
 2021.06.06 幸福公开课第一课随笔
 第二课第一周大作业--构建和评估一个线性风险模型