多任务学习——ICLR 2020PCGrad

Posted 2021-08-30 卓寿杰SoulJoy

论文：https://arxiv.org/pdf/2001.06782.pdf

在多任务学习中，由于不同任务梯度之间的更新方向不同，两个梯度在方向上存在冲突，从而导致一个不同任务之间的更新梯度存在冲突。

作者提出了PCGrad （projecting conflicting gradients），即将任务的梯度投影到具有冲突梯度的任何其他任务的梯度的法线平面上。 在一系列具有挑战性的多任务监督和多任务 RL 问题上，这种方法在效率和性能方面取得了实质性的进展。

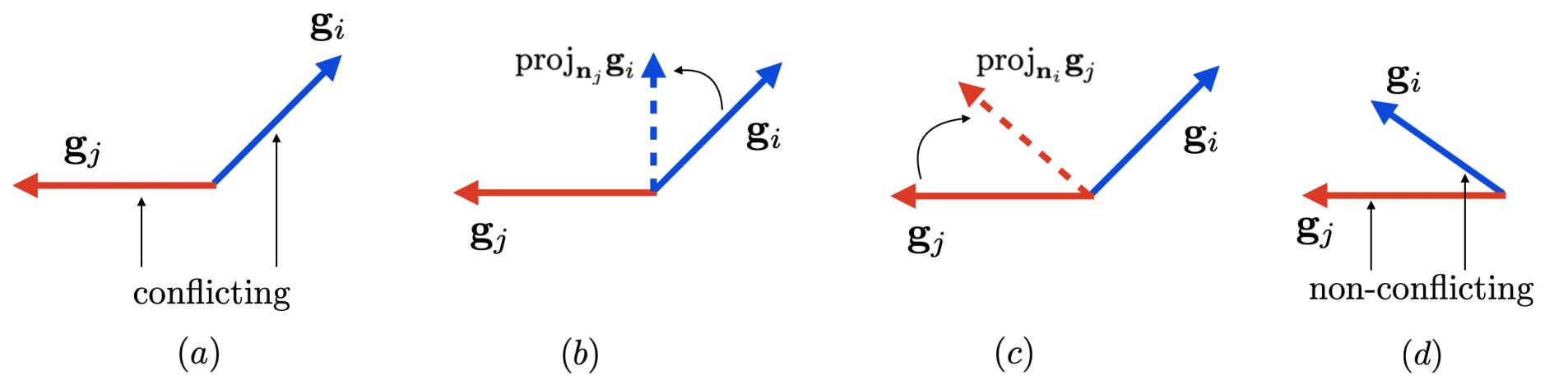
算法思想也比较简单：

• 首先，计算任务i梯度和随机一个其他任务j梯度之间的余弦相似度，如果为负值表示是相互冲突的梯度，如上图（a）
• 如果余弦相似度为负值，则通过下式计算任务i梯度在任务j梯度的法线平面上的投影（如上图（b））：
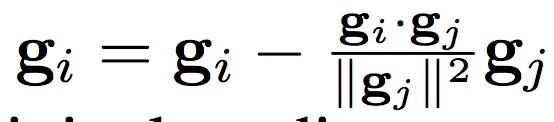
• 如果梯度没有冲突，即余弦相似度为非负，则直接使用原始梯度即可，如上图d。
• 选择另外一个任务，作为任务i，重复上述流程，直到所有任务的梯度都修正过一遍。
• 将各任务修正后的梯度相加，得到最终的梯度。
  
  这边我们来推导一下法平面的投影是如何计算的：
  

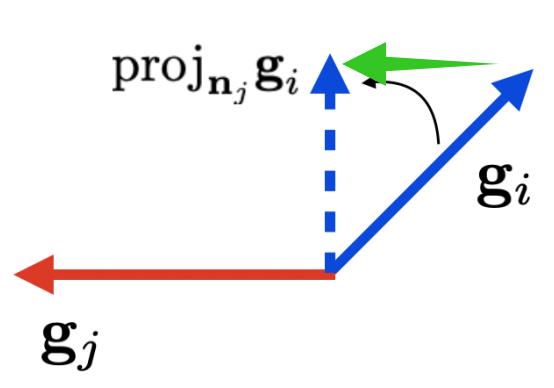
如上图， 我们设要求的投影向量（蓝色虚线）为$x$。绿色的向量和$g_j$同向，我们可以视它为$a{g}_j$。那么就有：
$x=g_i+a{g}_j$
$x{g}_j=(g_i+a{g}_j)g_j=g_i{g}_j+a||g_j|{|}^2=0$
即$a=-g_i{g}_j/||g_j||$
即$x=g_i-(g_i{g}_j/||g_j|{|}^2)g_j$

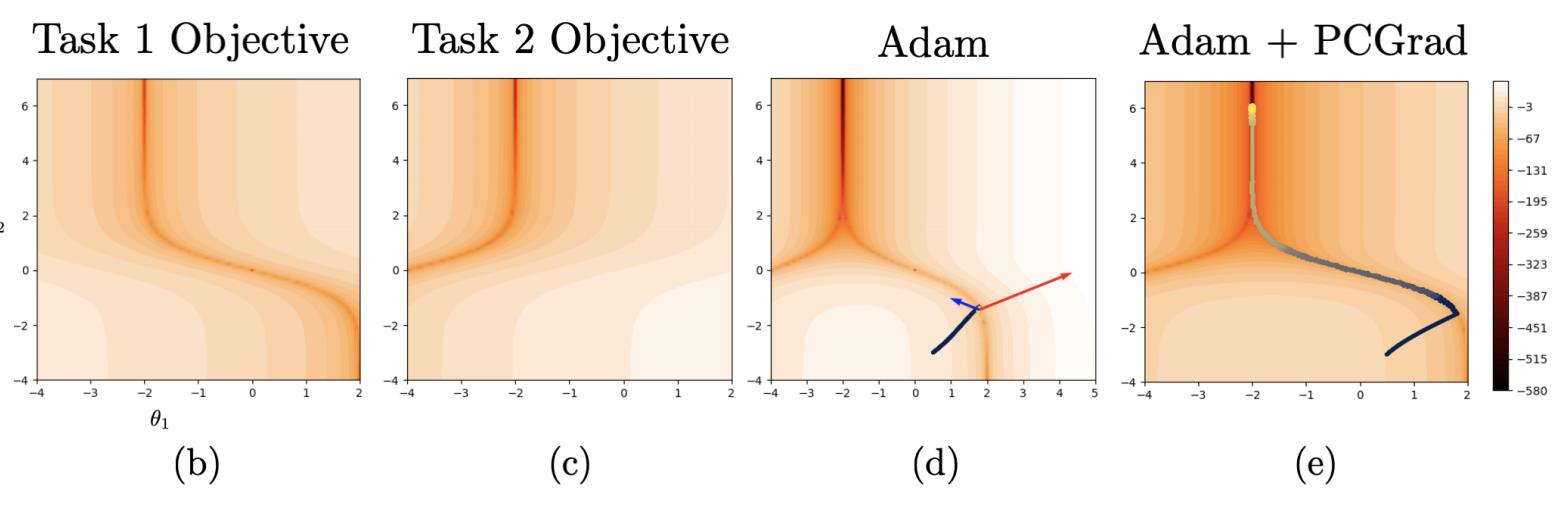
最后来看看效果吧~如下图所示，图b是任务1的目标的等高线图，图c是任务2的目标等高线图。图C是使用Adam优化目标梯度更新轨迹，可以看到当下时刻两个任务梯度方向是存在冲突的。而图e使用Adam+PCGrad，可以看到目标梯度更新轨迹穿越等高线就非常顺滑了。

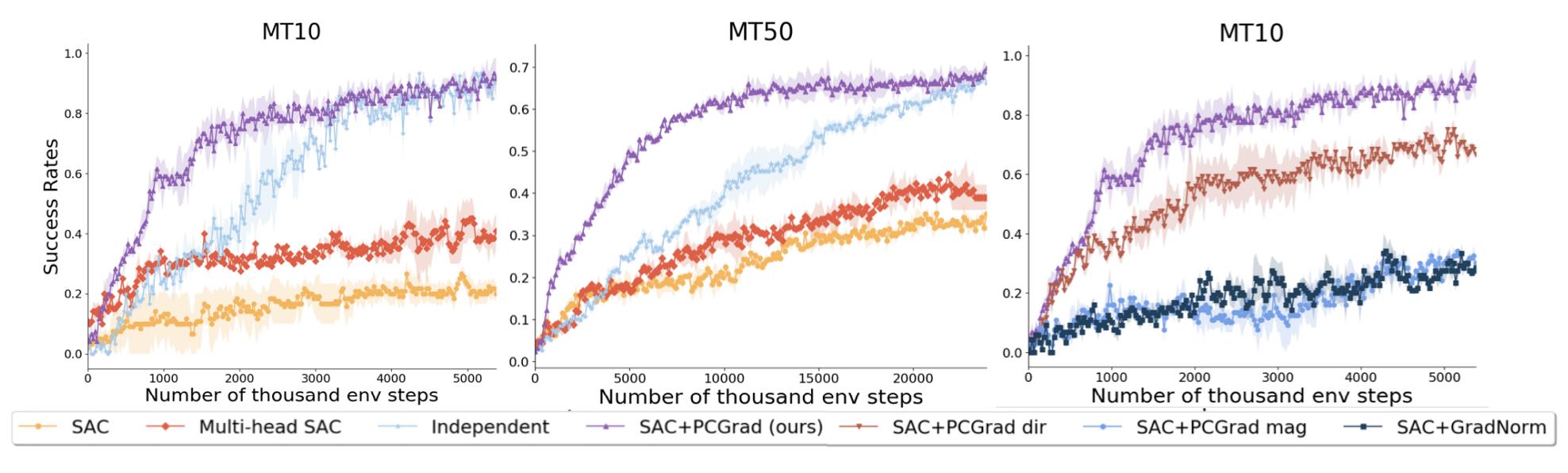
具体实验结果如下图，紫色为作者的结果。可以看到最终效果非常好，而且收敛很快：