马走日问题（Java版）

Posted 2021-08-30 ZSYL

这里写目录标题

• 问题描述
• 算法描述
• 参考代码

问题描述

给定 n*m 大小的棋盘，起点坐标（x, y），找出从起点开始，将棋盘所有位置走一遍，求总的方案数Sum.

限制条件：只能走日字型.

算法描述

我们都听过象棋中的马走日象走田，对于某一位置的棋子，总有8个方向可以选择，只有走日字且不超越棋盘大小，即可！

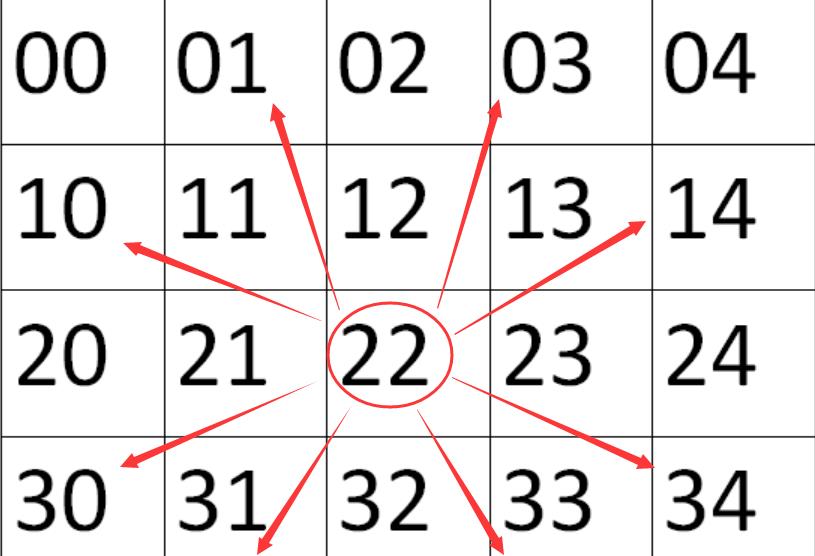
1. 方向设定

// 8个方向
int[] orient = {-1, 2, 1, -2, -1, -2, 1, 2, -1};  

2. 添加标记数组 vis[][]，标记某条路径（多叉树分支）的点，是否走过。

 boolean[][] vis = new boolean[n][m];;

3. sum：记录完成任务的总路径数。
4. curSum：当前路径上，经过的不同点数。
5. 当 curSum == n*m：即将棋盘所有位置遍历完成，即可sum++。
6. 注意：回溯 + 剪枝。

参考代码

import java.util.Scanner;

public class Main {
    static boolean[][] vis;  // 标记数组
    static int[] orient = {-1, 2, 1, -2, -1, -2, 1, 2, -1};  // 8个方向
    static int sum, n, m;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int t = sc.nextInt();
        while (t-- > 0) {
            // 矩阵图大小
            n = sc.nextInt();
            m = sc.nextInt();
            // 初始化标记数组，默认false
            vis = new boolean[n][m];
            // 获取起点坐标
            int x = sc.nextInt();
            int y = sc.nextInt();
            // 初始化，方案总数
            sum = 0;
            // 标记起点位置已经访问
            vis[x][y] = true;
            // 深度优先搜索：Go!
            dfs(x, y, 1);
            // 打印结果
            System.out.println(sum);
        }
    }
    public static void dfs(int x, int y, int curSum) {
        // 如果遍历完全部点，方案数 sum++，递归终止条件
        if (curSum == (n * m)) {
            sum++;
            return;
        }
        // 递归8个方向
        for (int i = 0; i < 8; i++) {
            // 获取可以到达的新方向
            int u = x + orient[i];
            int v = y + orient[i+1];
            // 剪枝条件，避免无效递归
            if (u < 0 || u >= n || v < 0 || v >= m || vis[u][v])
                continue;
            // 标记当前位置已访问
            vis[u][v] = true;
            // 继续往深处递归
            dfs(u, v, curSum+1);
            // 回溯
            vis[u][v] = false;
        }
    }
}

测试样例：

1
5 5 0 0

输出：

304