acm常见算法考点_线段树

Posted 2021-08-30 一只特立独行的猫

功能：
区间查询和单点修改。
线段树的本质就是采用空间换取时间的方式，将数组的每一个可能的区间的结果都存储到一个树里面，这样在查询是就很快。因为采用二叉树的形式存储，所以修改区间内一个值的也是log级别的。

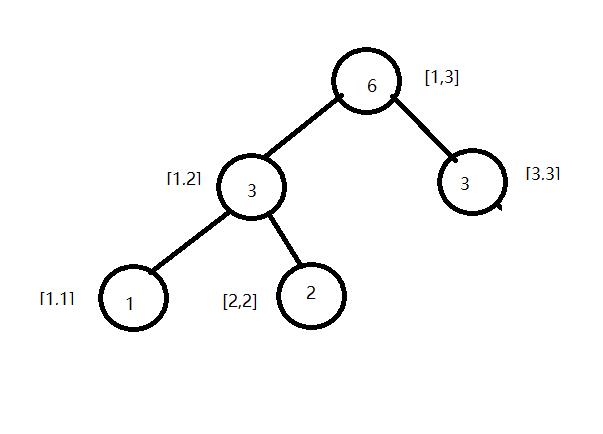
大概就是这样的一颗树，因为区间二分的平衡性，所以刚刚建立的一颗树肯定是一颗平衡树。所以为了方便，采用静态数组的方式存储树，类丝与堆的方式。
代码：

#include<iostream>

using namespace std;

const int N = 1e5 + 5;

int a[N],tree[N*2];
int n;

void build(int node,int start,int end) {
	if (start == end) {
		//修建根节点
		tree[node] = a[start];
		return;
	}
	int mid = start + end >> 1;
	int left_node = node * 2;
	int right_node = node * 2 + 1;
	build(left_node, start, mid);
	build(right_node, mid + 1, end);
	tree[node] = tree[right_node] + tree[left_node];
}

void updata(int node,int start,int end,int index,int val) {
	if (start == end) {
		//更新根节点
		a[index] = val;
		tree[node] = val;
		return;
	}
	int mid = start + end >> 1;
	int left_node = node * 2;
	int right_node = node * 2 + 1;
	if (index >= start && index <= mid) {
		updata(left_node, start, mid, index, val);
	}
	else if (index >= mid + 1 && index <= end) {
		updata(right_node, mid+1, end, index, val);
	}
	tree[node] = tree[left_node] + tree[right_node];
}

int query(int node, int start, int end,int L,int R) {
	if (start > R || end < L) {
		//区间无交集
		return 0;
	}
	if (start>=L&&end<=R) {
		return tree[node];
	}
	int left_node = node * 2;
	int right_node = node * 2 + 1;
	int mid = start + end >> 1;
	return query(left_node, start, mid, L, R) + query(right_node, mid + 1, end, L, R);
}

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	build(1, 1, n);
	int cnt;
	cin >> cnt;
	while (cnt--) {
		int k, x, y;
		cin >> k >> x >> y;
		if (k & 1) {
			cout << query(1, 1, n , x, y) << endl;
		}
		else {
			updata(1, 1, n , x, y);
		}
	}
	return 0;
}