(计算机组成原理)第二章数据的表示和运算-第二节5：定点数乘法运算（原码/补码一位乘法）

Posted 2021-08-30 快乐江湖

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了(计算机组成原理)第二章数据的表示和运算-第二节5：定点数乘法运算（原码/补码一位乘法）相关的知识，希望对你有一定的参考价值。

文章目录

一：乘法运算基本思想
二：原码一位乘法
- （1）实现原理
- （2）手算模拟
三：补码一位乘法（ $B o o t h$ 算法，考察重点）

一：乘法运算基本思想

关于定点数的乘法，其实我们在小学就学习过，就是经典列竖式相乘

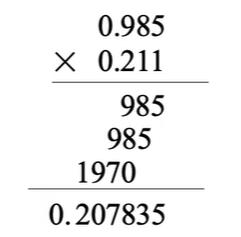
其中，我们印象最深的应该就是计算过程中的错位问题了。

在计算机中，相乘时使用的二进制，其基本逻辑和竖式相乘一致。如下是两个二进制数相乘，其中被乘数为 $0.1101$ ，乘数为 $0.1011$

我们将乘数看作为位权之和，即 $0.1011=1×2^{-1}+0×2^{-2}+1×2^{-3}+1×2^{-4}$
，被乘数写成 $a$ 与 $10^{n}$ 相乘的形式，即 $0.1101=1101×2^{-4}$

那么此乘法过程可以等价为下面的形式

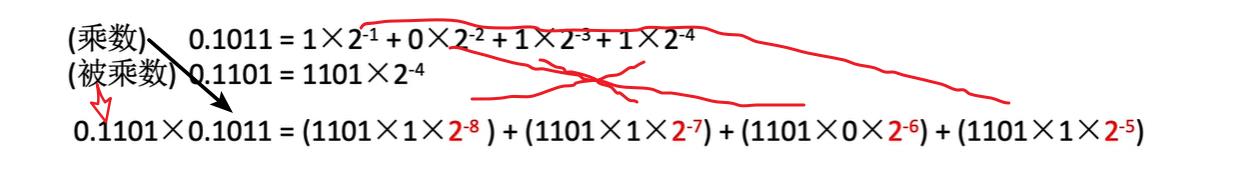
把竖式写全也就是下面的这个样子

由于二进制的乘数每一位只可能出现0或1，因此每次运算的结果要么是全0，要么只是被乘数乘以 $10^{n}$ ，实际结果只是小数点的不同，而计算机处理小数点位置非常方面，使用移位操作即可完成

二：原码一位乘法

（1）实现原理

逻辑看似很简单，但是如何让机器实现这是一个问题。如果要实现这一问题，必须解决以下三个问题

实际数字有正有负，符号位应当如何处理？
乘积运算时位数扩大很厉害，如何处理？
每次运算时的结果都要保存下来，如果相加？

其中符号位很方便处理，符号位 $x_{s}⊕y_{s}$ 即可判断，让数值位取绝对值进行乘法运算即可。

$c a s e ：$ 机器字长为 $n + 1 = 5$ 位， $x]_{原}=1.1101，[y]_{原}=0.1011$ ，采用原码一位乘法求 $x y$

还记得(计算机组成原理)第一章计算机系统概述-第二节：计算机硬件组成(存储器、运算器和控制器概述及计算机工作过程详解)这一节我们讲到过的运算器的组成吗，其中涉及乘法时会用到 $A C C$ ， $M Q$ ， $X$ 这三个寄存器

接下来我们详细叙述一下这个过程。开始， $x$ 是被乘数， $y$ 是乘数，因此 $x$ 位于X寄存器中， $y$ 位于MQ寄存器中，并且运算开始前要将ACC置为0

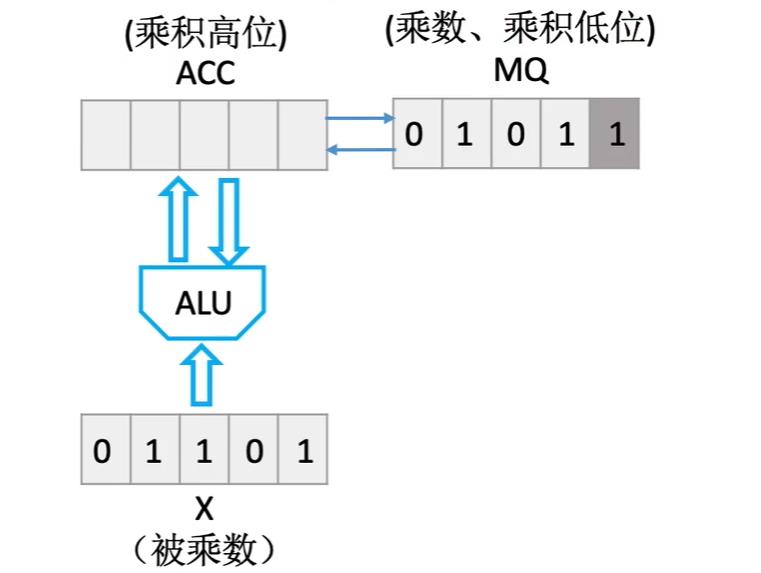
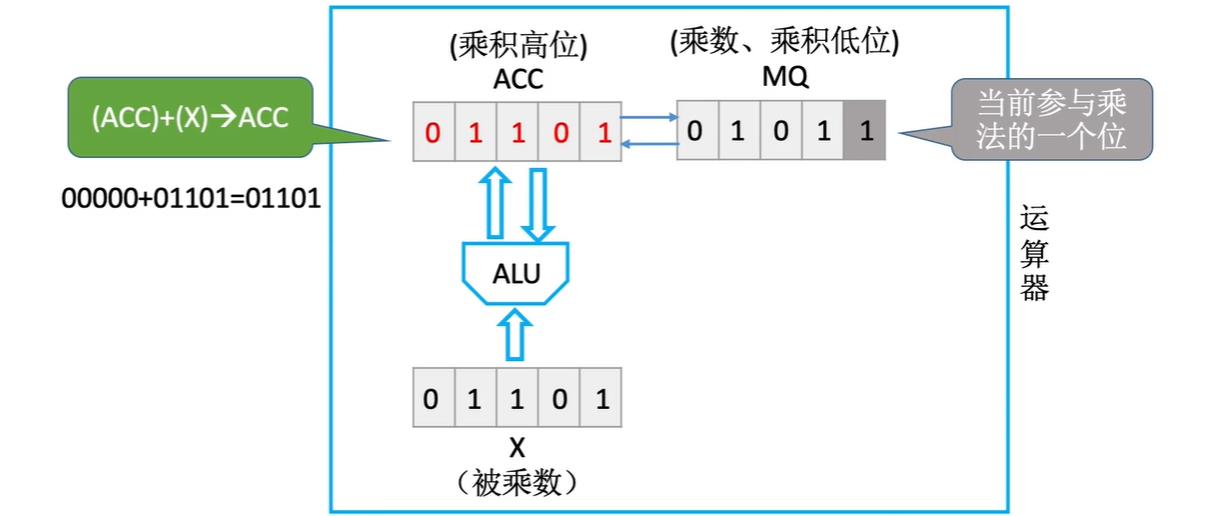
对应我们竖式乘法的逻辑，此时从低位到高位，依次用乘数的每一位乘被乘数，因此在这里进行第一次运算时我们把MQ寄存器中参与运算的那一位方块的颜色加深

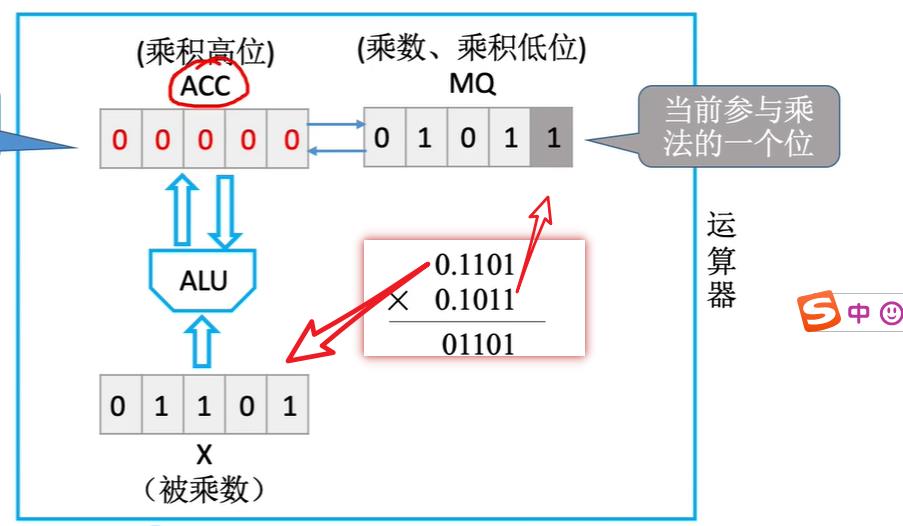
如果当前参与运算的乘数的这一位是1，则 $A C C$ 加上被乘数；如果当前位是0，则 $A C C$ 加上0，也即(ACC)+(X)->(ACC)

在进行下一位竖式运算时，必须偏移一个位置，对应于计算机处理时则是让ACC和MQ中的数据统一逻辑右移一位

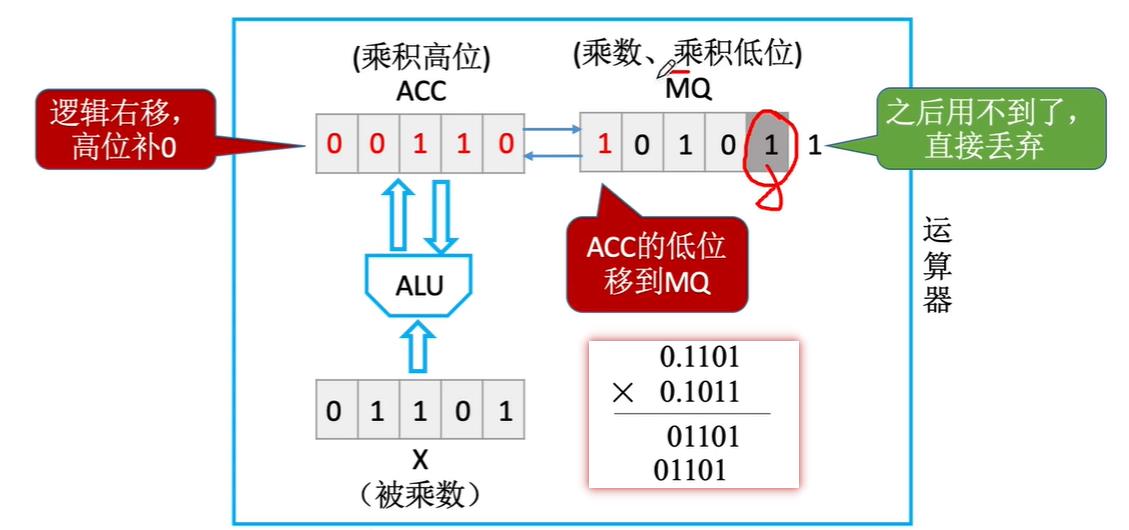
这样做本质实现的就是错误相加

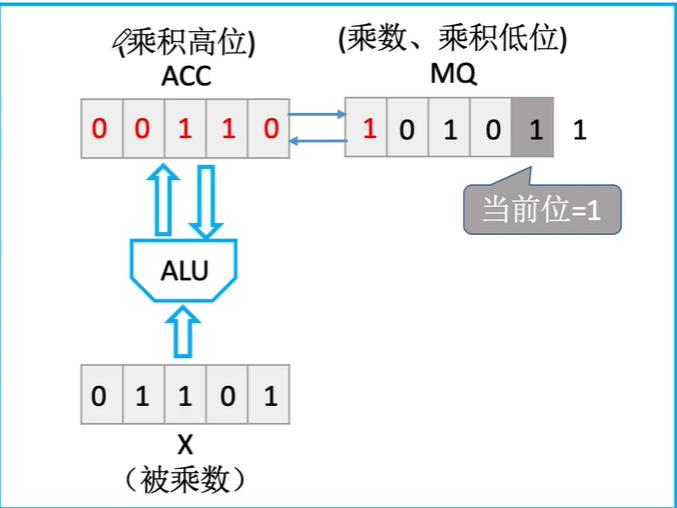
接着次低位来到了最低位的位置，再次进行(ACC)+(X)->(ACC)

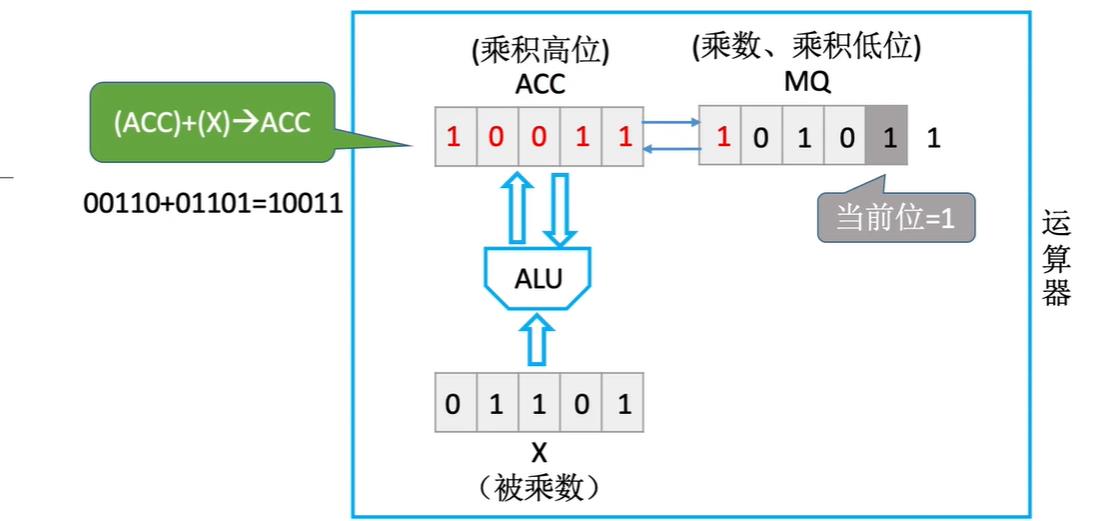
剩余的步骤均重复上述过程

（2）手算模拟

考试的时候，如果出到这样的题目，具体步骤如下
设 $X]_{原}=x_{s}$ ， $Y]_{原}=y_{s}$

被乘数和乘数均取绝对值参与运算，符号位为 $x_{s}⊕y_{s}$
部分积的长度同被乘数，取 $n + 1$ 位，以便存放乘法过程中绝对值大于等于的值，初值为 $0$
从乘数的最低位 $y_{n}$ 开始判断：若 $y_{n}=1$ ，则部分积加上被乘数 $∣ x ∣$ ，然后右移一位；若 $y_{n}=0$ ，则部分积加上0，然后右移一位。
重复步骤3，判断 $n$ 次

注意

由于乘积的数值部分是两数绝对值相乘的结果，因此原码一位乘法运算过程中的右移均为逻辑右移
考虑到运算时可能出现绝对值大于1的情况（但并非溢出），所以部分积和被乘数取双符号

$c a s e :$ 设机器字长为5位（ $n + 1$ ）, $x = - 0.1101$ ， $y = 0.1011$ ，采用原码一位乘法求解 $x y$

解： $∣ x ∣ = 00.1101$ , $∣ y ∣ = 00.1011$ ，过程如下

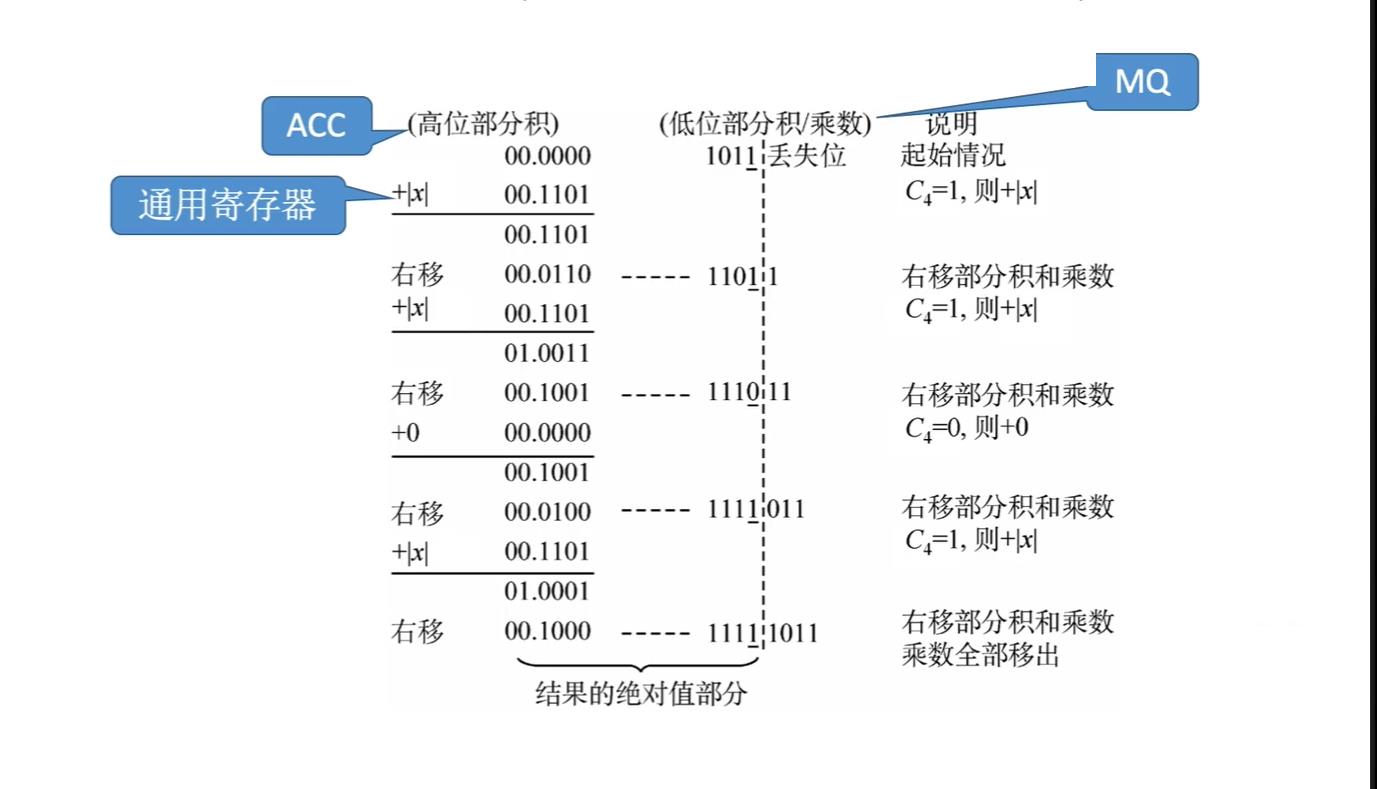
因此符号位为 $P_{s}=x_{s}⊕y_{s}=1=1⊕0=1$ ，得 $x \cdot y = - 0.10001111$

三：补码一位乘法（ $B o o t h$ 算法，考察重点）

定点数乘法中最有可能考察的便是补码一位乘法。因为机器做加减法时采用的是补码，倘若做乘法前再将补码转为原码，计算完成之后再转化为补码，那就很麻烦了，还不如直接用补码计算。

补码一位乘法主要分为校正法和比较法，校正法了解即可，而比较法（又叫 $B o o t h$ 算法）则是考察的重点。具体规则如下：

①：被乘数与部分积一般取双符号位，并且符号位参与运算。

一个原因是一旦符号位参与运算就一定要使用多符号位，因为一旦溢出，单符号位就会出错
另一个原因是，补码的右移时要看符号位而定的，如果采用单符号位，一旦数值部分的进位把符号给移掉了，下次移位就不知道该怎么办了。

②：乘数取单符号位以决定最后一步是否需要校正，也即是否需要加 $x]_{补}$
③：乘数末尾增设辅助位， $y_{n+1}$ ，初始值为0
④：根据 $y_{n}$ ， $y_{n+1}$ 判断位，进行运算，步骤和上面原码一位乘法一致
⑤：按上述算法进行n+1,其中最后一步也即n+1步不再一位，仅根据 $y_{0},y_{1}$ 比较结果决定是否需要加减 $x_[补]$

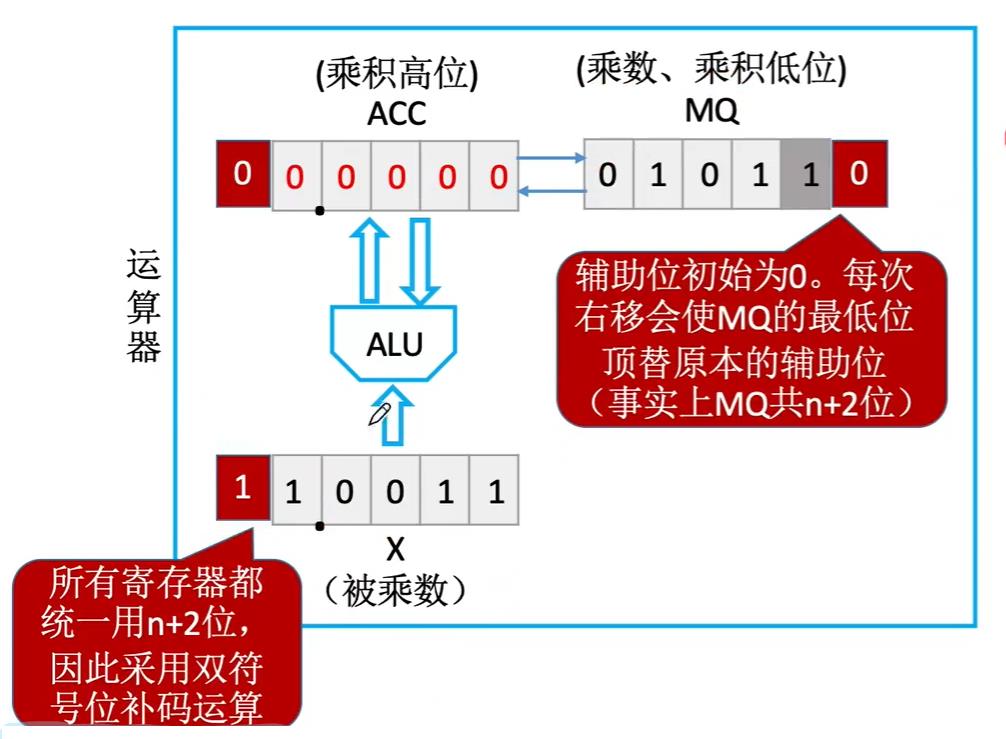
从上面图中大家可以看出MQ中的最低位现在是辅助位，这里就和原码乘法的最低位不一致了，所以这里我们用带有双引号的——“最低位”表示运算时真正的最低位，而不是辅助位

辅助位减“最低位”=1时， $ACC)+[x]_{补}$