李宏毅线性代数笔记13：SVD分解
Posted 刘文巾
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了李宏毅线性代数笔记13：SVD分解相关的知识，希望对你有一定的参考价值。
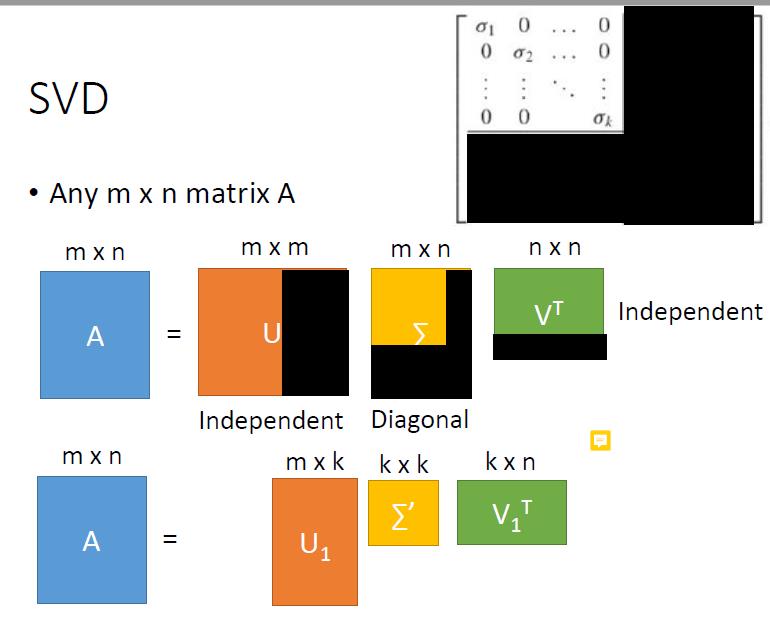
1 SVD分解介绍
之前用特征值来进行对角化的时候，被对角化的矩阵一定要是方阵，但是SVD的话，非方阵也是可以的。
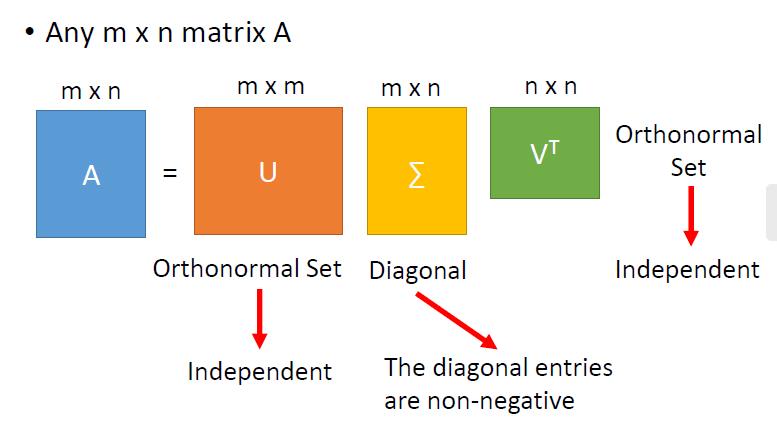
矩阵Σ对角线上的元素都是大于等于0的
我们可以改变U，V的一些行和列，来达到Σ对角线上的元素越来越小
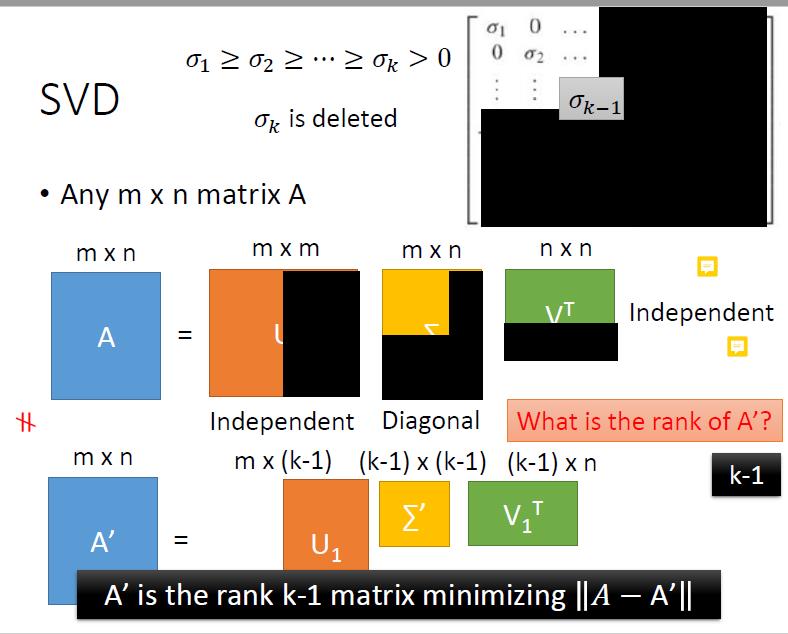
所以rank(A)就是Σ中对角线元素不为零的数量
如果把Σ中全零的部分抹掉，然后U和V中全零对应的行和列也去掉，那么乘积结果还是等于A
如果我们多抹掉一些（比如多抹掉一行），把Σ中非零的一部分也抹掉了，结果肯定不等于A了，但是是所有rank为k-1的部分中最接近于A的，接近的意思是两个矩阵相减的结果拉成一条向量，这个向量的norm最小
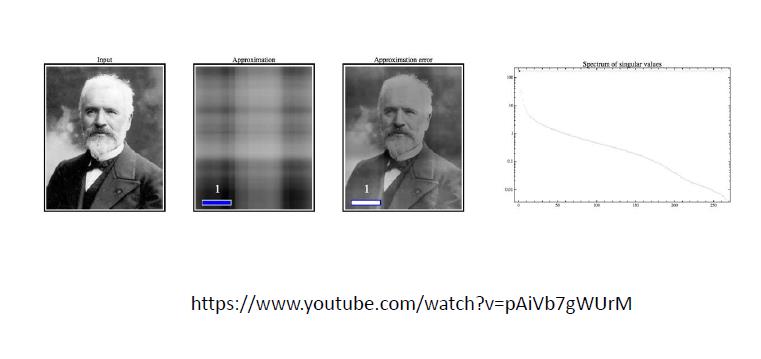
2 SVD的应用：图像压缩
可以用小一点的维度来复原一张相似的图
3 SVD求解
这里中间的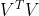
和
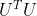可以消掉，是因为V和U是正交矩阵
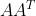和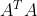
都是对称矩阵，那么我们就可以对其进行特征值分解（要变成标准正交基的那种，也就是特征值分解了之后，还要对特征空间的基进行施密特正交化）
然后Σ对角线的值就是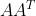或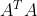的特征值的开方
以上是关于李宏毅线性代数笔记13：SVD分解的主要内容，如果未能解决你的问题，请参考以下文章