2021牛客多校5（部分题解）

Posted 2021-08-30 吃花椒的妙酱

B.Box

题目大意：每个盒子有01两种可能，打开盒子i要花费wi，也可以选择询问一次花费c，询问可以得知目前未打开的盒子里有多少个1，求得知所有序列的花费最小期望

思路：推式子

当c很大，w都很小时，显然直接打开所有盒子，花费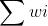

一般情况下，我们能确定下序列必定是本次盒子后缀全是0或者1，像00011111，然后我本次打开的是最后的那个0盒子，就可以确定下序列，我们算下后缀全是一个数的概率即可，因为我们求要开盒的概率即求不用开当前盒的概率，假设现在在第i个位置，后面还有n-i个盒子，什么时候截止到本次就不用开盒了呢，从i到n都是同色就不用开了，那这样的概率是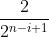，那要开的概率就是1-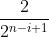。然后就是花费乘期望，就有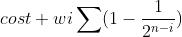

 然后和情况一取最小值

算概率的时候，到后面1/2^n其实很小，可以忽略= =

#include <cmath>
#include <cstring>
#include <algorithm>
#include <map>
#include <list>
#include <queue>
#include <vector>
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <deque>
using namespace std;
typedef long long ll;
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define scd(v) scanf("%d",&v)
#define scdd(a,b) scanf("%d %d",&a,&b)
#define endl "\\n"
#define IOS ios::sync_with_stdio(false)
#define pb push_back
#define all(v) v.begin(),v.end()
//#define int double
#define odd(x) x&1
#define mst(v,a) memset(v,a,sizeof(v))
#define lson p<<1 ,l,mid
#define rson p<<1|1,mid+1,r
#define ls p<<1
#define rs p<<1|1
const int N=1e5+10;
int n;
double c;
double a[N];
signed main()
{
    //!!
//   freopen("data.txt","r",stdin);
    //!!
//    IOS;
    cin>>n>>c;
    double sum=0;
    _for(i,1,n) cin>>a[i],sum+=a[i];
    sort(a+1,a+1+n,greater<double>());
    double temp=sum+c;
    double base=1;
    _for(i,1,min(n,60))
    {
       temp -= 1.0*a[i]/base;
       base*=2;
    }
    if( temp < sum )
    {
        printf("%.10lf",temp);
    }
    else printf("%.10lf",sum);
}

D. Double Strings

（题目都读错了

题目大意：两个字符串时好的，如果有相同前缀，一个不同字符(a<b)，后缀任意只要长度相同，求方案数

思路：dp、组合数

相同前缀用dp，dp[i][j]表示a串前i个字符与b串前j个字符有多少种相同前缀的匹配方案，

dp[i][j] = dp[i-1][j-1] + dp[i][j-1] + dp[i-1][j] + （a[i] == b[j]）*dp[i-1]dp[j-1]

如果当前字符相同，贡献还要加上dp[i-1][j-1]

求后缀的话，假设现在位置在a串第i位。b串第j位，a串还剩len1-i设为x , b还剩len2-j（设为y）位没匹配，接下来挑选任意后缀，不妨设x<=y，则有公式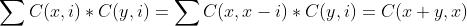

最后一步，x中选x-i个，y中选i个，一共选x个，所以可以合并

#include <cmath>
#include <cstring>
#include <algorithm>
#include <map>
#include <list>
#include <queue>
#include <vector>
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <deque>
using namespace std;
typedef long long ll;
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define scd(v) scanf("%d",&v)
#define scdd(a,b) scanf("%d %d",&a,&b)
#define endl "\\n"
#define IOS ios::sync_with_stdio(false)
#define pb push_back
#define all(v) v.begin(),v.end()
#define int long long
#define odd(x) x&1
#define mst(v,a) memset(v,a,sizeof(v))
#define lson p<<1 ,l,mid
#define rson p<<1|1,mid+1,r
#define ls p<<1
#define rs p<<1|1
const int N = 1e4 + 10;
const int mod = 1e9 + 7;
int n, m;
int len1, len2;
char s1[N], s2[N];
int dp[5010][5010];
int f[15010];
int ni[15010];
ll qsm(int a, int b)
{
    int ans = 1, temp = a;
    while (b)
    {
        if (b & 1) ans = (ans * temp) % mod; 
        temp = (temp * temp) % mod;
        b>>=1;
    }
    return ans;
}
ll C(int n ,int m)
{
    if( m>n || m<0) return 0;
    if( m==0  || n == m) return 1;
    return f[n] * ni[n-m] %mod * ni[m]%mod;
}
void debug()
{
    cout<<len1<<" len "<<len2<<endl;
}
void solve()
{
    _for(i, 1, len1)
    {
        _for(j, 1, len2)
        {
            dp[i][j] = dp[i][j - 1] + dp[i - 1][j] - dp[i - 1][j - 1];
            if (s1[i] == s2[j]) dp[i][j] += dp[i - 1][j - 1] + 1;
            if(dp[i][j]<0) dp[i][j] += mod;
            if(dp[i][j]>=mod)dp[i][j]%=mod;
        }
    }
    int ans = 0;
    _for(i, 1, len1)
    {
        _for(j, 1, len2)
        {
            if( s1[i] < s2[j] )
            {
               // cout<<i<<" "<<j<<endl;
                int x = len1 - i;
                int y = len2 - j;
                ans += (dp[i-1][j-1]+1) * C(x + y, min(x, y))%mod;
                ans %= mod;
            }
        }
    }
    cout<<ans%mod<<endl;
    //debug();
}
signed main()
{
    //!!
//   freopen("data.txt","r",stdin);
    //!!
    IOS;
    f[0] = 1;
    _for(i, 1, 15000) f[i] = f[i - 1] * i % mod;
    _for(i, 0, 15000) ni[i] = qsm(f[i], mod - 2);
    cin >> (s1 + 1);
    cin >> (s2 + 1);
    len1 = strlen(s1 + 1);
    len2 = strlen(s2 + 1);
    solve();
}

H

我的构造是

010101

010101

101010

101010

K

思路：st表优化+双指针

对于区间而言，极差是有单调性的，如果当前区间满足某极差，对这个区间延伸，极差仍然满足。

枚举区间左界，右界移动指针，右指针找到一个满足位置就停止，下一个左界，右指针不用回头，只要继续右移，这样一遍的复杂度为O(n)，总复杂度为O(nm)

st表的查询的log函数需要预处理掉！！被这个坑惨了，一直以为我的st表是O(1)查询，带个log直接tle了。

顺便说一句二分会tle，然后还有单调队列的做法