数据结构 时间复杂度与空间复杂度

Posted 2021-08-30 一个正直的男孩

开辟新篇章，数据结构与算法，要想走的更远那么一定要学数据结构，如果你掌握了他，写的代码会得到很大的优化！！！

---

❓什么是数据结构与算法

🙊：数据结构

• 数据结构 = 数据元素 + 元素之间的关系
• 常见的有以下这些类型
  

🙊：算法

• 算法是特定问题求解步骤的描述,算法是独立语言而存在的一种解决问题的方法和思想
• 常见的算法
  

🤔：他们之间的关系

• 算法是依赖着数据结构的，数据结构是算法的基础，俩者缺一不可。

❓ 时间复杂度与空间复杂度

• 衡量一个算法的好坏有俩个方面

1. 时间复杂
2. 空间复杂度

⌛️ 时间复杂度

时间复杂度并不是他运行时所占用的了多少时间，而是他在算法中基本操作了多少次

🤯：如何计算时间复杂度

• 算出他执行了多少次，取他大概执行了多少次（算法执行做多的那次），然后用O的渐进表示法
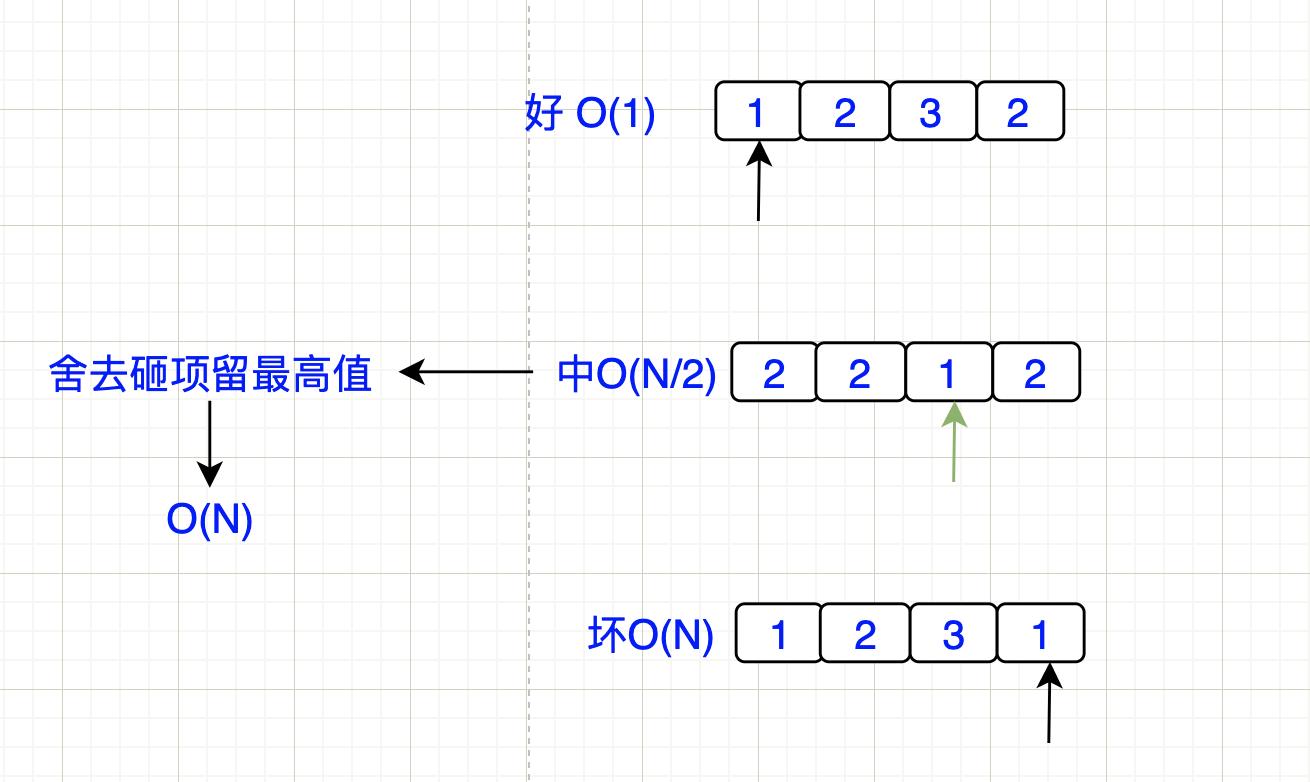
• 如果算法中时执行了常数次（数得清），那么用O(1)表示
• 去掉影响不大的值，取最大项（在最大项无限大的时候那么其他的附庸值就不是那么重要）
• 算法一定要取最坏的情况（保底思路）
  

⌨️：案例

🧐：解析

• 第一个循环2n,后一个为10
• 2N+10，舍去杂项取最高次
  O(N)

🙉：代码

void Func2(int N)
{
    int count = 0;
    for (int k = 0; k < 2 * N ; ++ k)//2n
    {
++count;
 }
    int M = 10;
    while (M--)//10
    {
++count;
 }
    printf("%d\\n", count);
}

🧐：解析

• 第一个循环M,后一个为N
• O(M+N),都是未知次其实取哪一个都一样，也可以写成O(max(M,N))

🙉：代码

void Func3(int N, int M) {
    int count = 0;
    for (int k = 0; k < M; ++ k)
    {
++count; }
    for (int k = 0; k < N ; ++ k)
    {
++count; }
    printf("%d\\n", count);
}

🧐：解析

• 第一个循环100
• 只要时数字就是常数次
  O(1)

🙉：代码

void Func4(int N)
{
    int count = 0;
    for (int k = 0; k < 100; ++ k)//100数字，常数
    {
++count; }
    printf("%d\\n", count);
}

🧐：解析

• N(logN)
  

🙉：代码

nt BinarySearch(int* a, int n, int x) {
assert(a);
    int begin = 0;
    int end = n-1;
    while (begin < end)
    {
        int mid = begin + ((end-begin)>>1);
        if (a[mid] < x)
            begin = mid+1;
        else if (a[mid] > x)
            end = mid;
        else
   } 
   return 0;
}

🧐：解析

• O(N)
• 每次递归n-1，执行了n次

🙉：代码

long long Fac(size_t N)
{
    if(0 == N)
        return 1;
    return Fac(N-1)*N;
}

🧐：解析

• O(2^N)
• 他的意义不大，2^N算是算法中的凤姐级别了
  

🙉：>代码

long long Fib(size_t N)
{
    if(N < 3)
        return 1;
    return Fib(N-1) + Fib(N-2);
}

🔭 空间复杂度

• 他是在算法中零时开辟了多少变量
• 一般来讲都是O(1)
• 表示法和时间复杂度差不多
• 现在堆空间复杂度要求不高，现在每个电脑不是基本都是好几百个G或者几个T
• 摩尔定理，没各18月性能翻倍
  

⌨️：案例

🧐：解析

• O（1）只创建了俩个变量

🙉：代码

void Func4(int N)
{
    int count = 0;
    for (int k = 0; k < 100; ++ k)//100数字，常数
    {
++count; }
    printf("%d\\n", count);
}

🧐：解析

• O（N),开辟了N个元素

🙉：代码

int *a =(int *)malloc(n*sizeof(int )) 

🧐：解析

• O（N),开辟了N个元素
• 每次呀栈都是消耗内存的

🙉：代码

long long Fac(size_t N)
{
    if(N == 0)
        return 1;
    return Fac(N-1)*N;
}

🧐：解析

• O（N),开辟了N个元素
• 空间时可以重复利用，但是时间不可以

🙉：代码

long long* Fibonacci(size_t n) {
    if(n==0)
         return NULL;
    long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
    fibArray[0] = 0;
    fibArray[1] = 1;
    for (int i = 2; i <= n ; ++i)
    {
        fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
    return fibArray;
}