背包九讲 整理
Posted iuk11
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了背包九讲 整理相关的知识,希望对你有一定的参考价值。
该篇文章为了自己回顾基础,也为了下学期为社团讲解做个铺垫,本来想做ppt但是公式真是太折磨人了。
主要是自己太菜了,想一直刷题,发现到后面想不出来,看题解也要看半天,仔细回想觉得是因为经典问题不牢固的原因。
所有解题思路学习来源于acwing。
01背包问题
问题叙述:
有
n
n
n 件物品和一个容量为
v
v
v 的背包,每件物品只能选择一次。
对于第
i
i
i 件物品,体积为
v
[
i
]
v[i]
v[i] ,价值为
w
[
i
]
w[i]
w[i] 。
问不超过背包容量的情况下,拿哪些物品得到的总价值最大。
问题分析:
采用闫式dp分析法,在集合的角度进行分析 (状态表示:
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] )。
集合:只考虑前
i
i
i 个物品在容量为
j
j
j 的背包下,拿到的最大价值。
属性:Max.
集合划分:如图
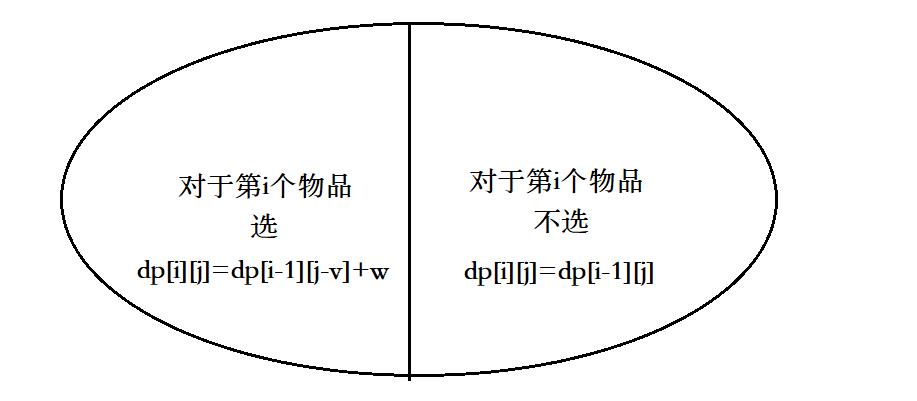
得到状态转移方程:
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
]
,
d
p
[
i
−
1
]
[
j
−
v
]
+
w
)
dp[i][j]=max(dp[i-1][j],dp[i-1][j-v]+w)
dp[i][j]=max(dp[i−1][j],dp[i−1][j−v]+w)
完整代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
int v,w;
int dp[1010][1010];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>v>>w;
for(int j=0;j<=m;j++){
dp[i][j]=dp[i-1][j];
if(j-v>=0) dp[i][j]=max(dp[i][j],dp[i-1][j-v]+w);
}
}
cout<<dp[n][m]<<endl;
return 0;
}
优化空间:
由上文分析可知,所有的
[
i
]
[i]
[i] 都是由
[
i
−
1
]
[i-1]
[i−1] 转移来的。那么可以用滚动数组代替第一维 or 可以把体积由大到小枚举,这样在判断的时候当前物品的时候,
[
i
]
[i]
[i]中的状态还没有更新,相当于
[
i
−
1
]
[i-1]
[i−1] 。
//滚动数组方法
#include<bits/stdc++.h>
using namespace std;
int n,m;
int v,w;
int dp[2][1010];
int id;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>v>>w;
id^=1;
for(int j=0;j<=m;j++){
dp[id][j]=dp[id^1][j];
if(j-v>=0) dp[id][j]=max(dp[id][j],dp[id^1][j-v]+w);
}
}
cout<<dp[id][m]<<endl;
return 0;
}
//一维数组写法
#include<bits/stdc++.h>
using namespace std;
int n,m;
int v,w;
int dp[1010];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>v>>w;
for(int j=m;j>=v;j--){
dp[j]=max(dp[j],dp[j-v]+w);
}
}
cout<<dp[m]<<endl;
return 0;
}
完全背包问题
问题叙述:
有
n
n
n 件物品和一个容量为
v
v
v 的背包,每件物品可以选择无数次。
对于第
i
i
i 件物品,体积为
v
[
i
]
v[i]
v[i] ,价值为
w
[
i
]
w[i]
w[i] 。
问不超过背包容量的情况下,拿哪些物品得到的总价值最大。
问题分析:
采用闫式dp分析法,在集合的角度进行分析 (状态表示:
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] )。
集合:只考虑前
i
i
i 个物品在容量为
j
j
j 的背包下,拿到的最大价值。
属性:Max.
集合划分:如图

更正:不是 k 种选法,是 k*v 不大于 j 种选法
得到状态转移方程:
d
p
[
i
]
[
j
]
=
m
a
x
{
d
p
[
i
−
1
]
[
j
−
k
∗
v
]
+
k
∗
w
}
dp[i][j]=max\\{dp[i-1][j-k*v]+k*w\\}
dp[i][j]=max{dp[i−1][j−k∗v]+k∗w}
k
=
0
,
1
,
2...
k=0,1,2...
k=0,1,2...
//三维写法 时间复杂度O(n^3)
#include<bits/stdc++.h>
using namespace std;
int n,m;
int v,w;
int dp[1010][1010];
int main(){
ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>v>>w;
for(int j=0;j<=m;j++){
for(int k=0;k*v<=j;k++){
dp[i][j]=max(dp[i][j],dp[i-1][j-k*v]+k*w);
}
}
}
cout<<dp[n][m];
return 0;
}
因为上一个写法的时间复杂度太大,我们对状态转移方程再次进行整理,得到: d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j − v ] + w , d p [ i − 1 ] [ j − 2 ∗ v ] + 2 ∗ w + d p [ i − 1 ] [ j − 3 ∗ v ] + 3 ∗ w . . . ) dp[i][j]=max(dp[i-1][j-v]+w,dp[i-1][j-2*v]+2*w+dp[i-1][j-3*v]+3*w...) dp[i][j]=max(dp[i−1][j−v]+w,dp[i−1][j−2∗v]+2∗w+dp[i−1][j−3∗v]+3∗w...) d p [ i ] [ j − v ] = m a x ( d p [ i − 1 ] [ j − 2 ∗ v ] + w , d p [ i − 1 ] [ j − 3 ∗ v ] + 2 ∗ w . . . ) dp[i][j-v]=max(dp[i-1][j-2*v]+w,dp[i-1][j-3*v]+2*w...) dp[i][j−v]=max(dp[i−1][j−2∗v]+w,dp[i−1][j−3∗v]+2∗w...)由两公式得到: d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − v ] + w ) dp[i][j]=max(dp[i-1][j],dp[i][j-v]+w) dp[i][j]=max(dp[i−1][j],dp[i][j−v]+w)解释: d p [ i ] [ j ] dp[i][j] dp[i][j] 的最大值为不选或者选一个的最大值,因为选一个的最大值,就是选一个或者选两个的最大值…
#include<bits/stdc++.h>
using namespace std;
int n,m;
int v,w;
int dp[1010][1010];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>v>>w;
for(int j=0;j<=m;j++){
dp[i][j]=dp[i-1][j];
if(j-v>=0) dp[i][j]=max(dp[i-1][j],dp[i][j-v]+w);
}
}
cout<<dp[n][m];
return 0;
}
最后再优化一下空间:
对于为什么dp[j]可以表示
[
i
−
1
]
[i-1]
[i−1]的状态,可以思考一下,从小到大枚举的意义。
#include以上是关于背包九讲 整理的主要内容,如果未能解决你的问题,请参考以下文章