「深度学习一遍过」必修8:搭建卷积神经网络 LeNet-5
Posted 荣仔!最靓的仔!
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了「深度学习一遍过」必修8:搭建卷积神经网络 LeNet-5相关的知识,希望对你有一定的参考价值。
本专栏用于记录关于深度学习的笔记,不光方便自己复习与查阅,同时也希望能给您解决一些关于深度学习的相关问题,并提供一些微不足道的人工神经网络模型设计思路。
专栏地址:「深度学习一遍过」必修篇
目录
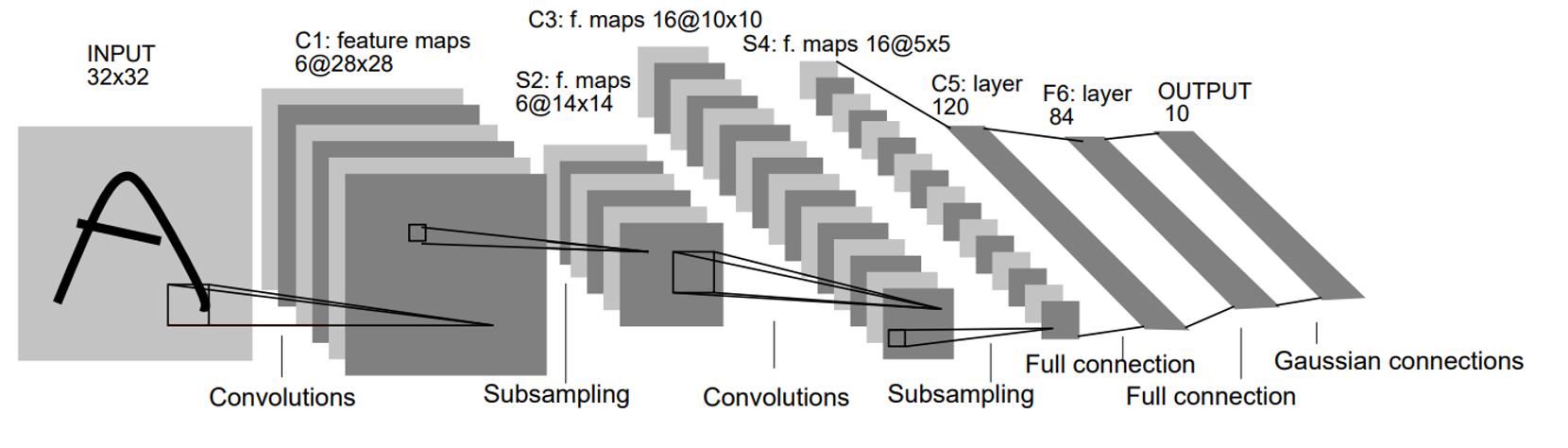
1 LeNet-5 的网络结构与特点
- 所有卷积核均为
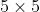 ,步长为
,步长为 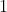
- 所有池化方法为平均池化
- 所有计划函数采用
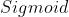
2 各层参数详解
LeNet-5 共有 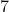 层,不包含输入,每层都包含可训练参数;每个层有多个 Feature Map,每个 FeatureMap 通过一种卷积滤波器提取输入的一种特征,然后每个 FeatureMap 有多个神经元。
层,不包含输入,每层都包含可训练参数;每个层有多个 Feature Map,每个 FeatureMap 通过一种卷积滤波器提取输入的一种特征,然后每个 FeatureMap 有多个神经元。
2.1 INPUT 层——输入层
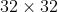 。
。
2.2 C1 层——卷积层
- 输入图片:
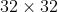
- 卷积核大小:
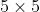
- 卷积核种类:
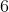
- 输出特征图大小:
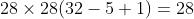
- 神经元数量:
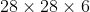
- 可训练参数:
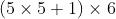 (每个滤波器
(每个滤波器  个
个 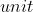 参数和一个
参数和一个 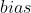 参数,一共
参数,一共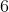 个滤波器)
个滤波器) - 连接数:
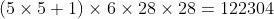
2.3 S2 层——池化层(下采样层)
- 输入:
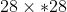
- 采样区域:
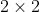
- 采样方式:
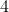 个输入相加,乘以一个可训练参数,再加上一个可训练偏置。结果通过
个输入相加,乘以一个可训练参数,再加上一个可训练偏置。结果通过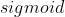
- 采样种类:
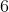
- 输出特征图大小:
- 神经元数量:
- 连接数:
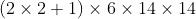
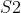 中每个特征图的大小是
中每个特征图的大小是 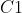 中特征图大小的
中特征图大小的  。
。
2.4 C3 层——卷积层
- 输入:
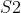 中所有
中所有 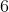 个或者几个特征图组合
个或者几个特征图组合 - 卷积核大小:
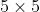
- 卷积核种类:
- 输出特征图大小:
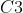 中的每个特征 map 是连接到
中的每个特征 map 是连接到 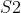 中的所有
中的所有 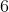 个或者几个特征 map 的,表示本层的特征 map 是上一层提取到的特征 map 的不同组合存在的一个方式是:C3 的前 6 个特征图以 S2 中 3 个相邻的特征图子集为输入。接下来 6 个特征图以 S2 中 4 个相邻特征图子集为输入。然后的 3 个以不相邻的 4 个特征图子集为输入。最后一个将 S2 中所有特征图为输入。
个或者几个特征 map 的,表示本层的特征 map 是上一层提取到的特征 map 的不同组合存在的一个方式是:C3 的前 6 个特征图以 S2 中 3 个相邻的特征图子集为输入。接下来 6 个特征图以 S2 中 4 个相邻特征图子集为输入。然后的 3 个以不相邻的 4 个特征图子集为输入。最后一个将 S2 中所有特征图为输入。
- 可训练参数:

- 连接数:
第一次池化之后是第二次卷积,第二次卷积的输出是 C3,16 个 
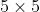 。我们知道 S2 有 6 个
。我们知道 S2 有 6 个 
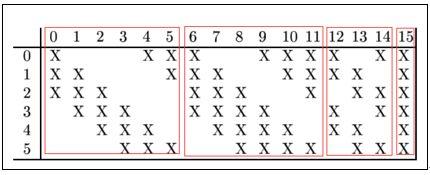
C3 的前 6 个特征图(对应上图第一个红框的 6 列)与 S2 层相连的 3 个特征图相连接(上图第一个红框),后面 6 个特征图与 S2 层相连的 4 个特征图相连接(上图第二个红框),后面 3 个特征图与 S2 层部分不相连的 4 个特征图相连接,最后一个与 S2 层的所有特征图相连。卷积核大小依然为 5*5。
所以总共有  个参数。而图像大小为
个参数。而图像大小为 

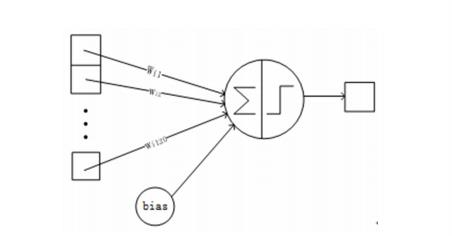
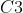 与
与 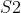 中前
中前 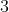 个图相连的卷积结构如下图所示:
个图相连的卷积结构如下图所示:
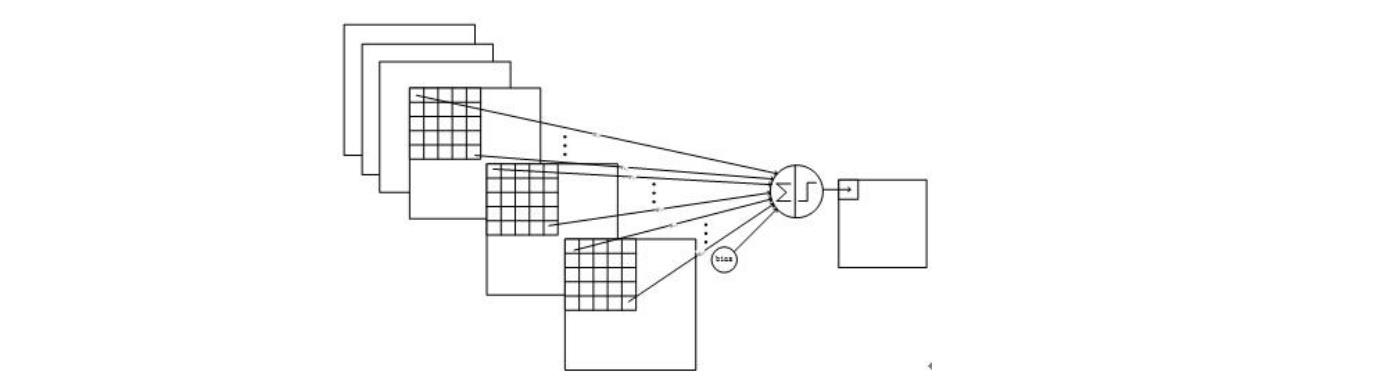
2.5 S4 层——池化层(下采样层)
- 输入:
- 采样区域:
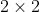
- 采样方式:
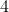 个输入相加,乘以一个可训练参数,再加上一个可训练偏置。结果通过
个输入相加,乘以一个可训练参数,再加上一个可训练偏置。结果通过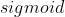
- 采样种类:
- 输出特征图大小:

- 神经元数量:

- 连接数:
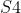 中每个特征图的大小是C3中特征图大小的
中每个特征图的大小是C3中特征图大小的 
2.6 C5 层——卷积层
- 输入:
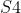 层的全部
层的全部 个单元特征map(与
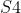 全相连)
全相连) - 卷积核大小:
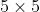
- 卷积核种类:
- 输出特征图大小:

- 可训练参数/连接:
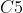 层是一个卷积层。由于
层是一个卷积层。由于 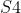 层的
层的  个图的大小为
个图的大小为 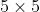 ,与卷积核的大小相同,所以卷积后形成的图的大小为
,与卷积核的大小相同,所以卷积后形成的图的大小为  。这里形成
。这里形成  个卷积结果。每个都与上一层的
个卷积结果。每个都与上一层的  个图相连。所以共有
个图相连。所以共有 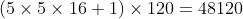 个参数,同样有
个参数,同样有  个连接。
个连接。 层的网络结构如下:
层的网络结构如下:
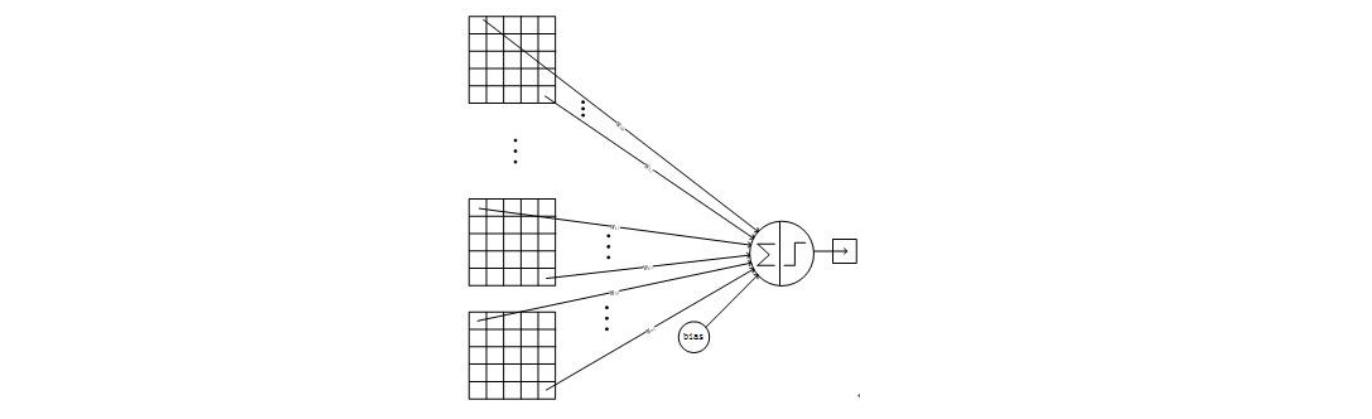
2.7 F6 层——全连接层
- 输入:
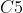
维向量
- 计算方式:计算输入向量和权重向量之间的点积,再加上一个偏置,结果通过
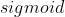 函数输出。
函数输出。 - 可训练参数:
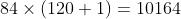
F6 层是全连接层。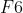 层有
层有 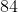 个节点,对应于一个
个节点,对应于一个  的比特图,
的比特图,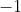 表示白色,
表示白色,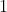 表示黑色,这样每个符号的比特图的黑白色就对应于一个编码。该层的训练参数和连接数是
表示黑色,这样每个符号的比特图的黑白色就对应于一个编码。该层的训练参数和连接数是 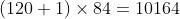 。
。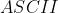 编码图如下:
编码图如下:

2.8 Output 层——全连接层
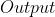 层也是全连接层,共有
层也是全连接层,共有  个节点,分别代表数字
个节点,分别代表数字 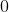 到
到 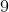 ,且如果节点
,且如果节点  的值为
的值为 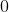 ,则网络识别的结果是数字
,则网络识别的结果是数字  。采用的是径向基函数(
。采用的是径向基函数(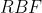 )的网络连接方式。假设
)的网络连接方式。假设 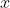 是上一层的输入,
是上一层的输入,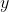 是
是 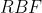 的输出,则
的输出,则 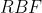 输出的计算方式是:
输出的计算方式是:

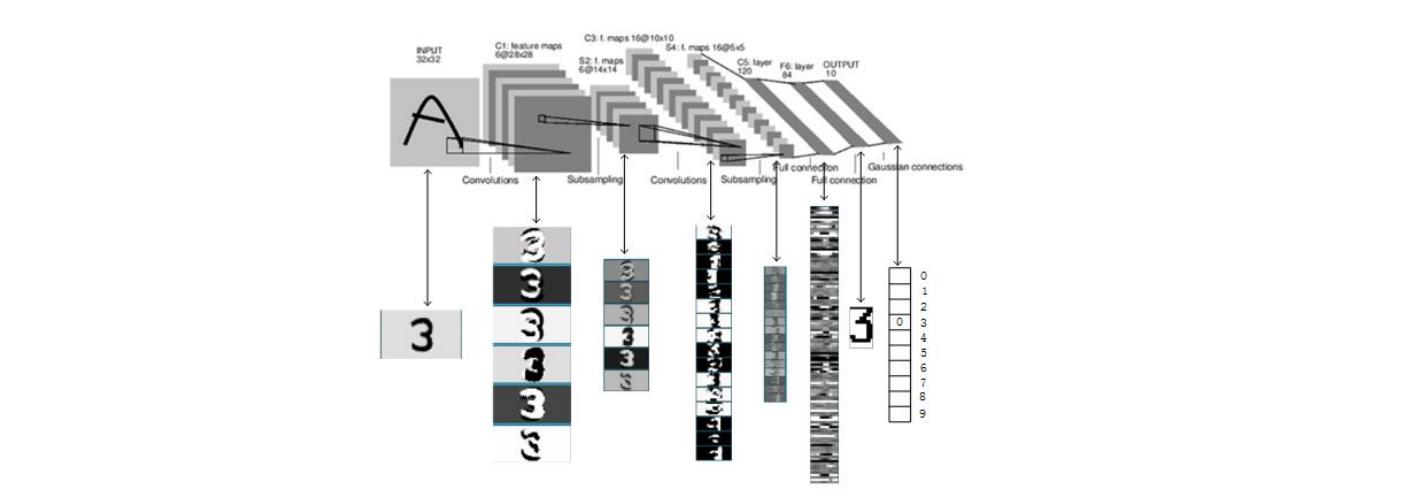
下图是 LeNet-5 识别数字 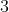 的过程:
的过程:
3 代码实现
import torch
from torch import nn
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision.transforms import ToTensor
# 查看pytorch版本
print(torch.__version__)
# 下载数据集
training_data = datasets.FashionMNIST(
root="data",
train=True,
download=True,
transform=ToTensor()
)
test_data = datasets.FashionMNIST(
root="data",
train=False,
download=True,
transform=ToTensor()
)
batch_size = 32
train_dataloader = DataLoader(training_data, batch_size=batch_size)
test_dataloader = DataLoader(test_data, batch_size=batch_size)
print(train_dataloader)
for X, y in test_dataloader:
print(X.shape)
print(y.shape)
break
device = "cuda" if torch.cuda.is_available() else "cpu"
class MyLeNet(nn.Module):
def __init__(self):
super(MyLeNet, self).__init__()
self.c1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=2)
self.relu = nn.ReLU()
self.s2 = nn.AdaptiveAvgPool2d(14)
self.c3 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5, stride=1)
self.s4 = nn.AdaptiveAvgPool2d(5)
self.flatten = nn.Flatten()
self.c5 = nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5)
self.f6 = nn.Linear(120, 84)
self.output = nn.Linear(84, 10)
def forward(self, x):
x = self.relu(self.c1(x))
x = self.s2(x)
x = self.relu(self.c3(x))
x = self.s4(x)
x = self.c5(x)
x = self.flatten(x)
x = self.f6(x)
x = self.output(x)
return x
model = MyLeNet().to(device)
print(model)
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)
def train(dataloader, model, loss_fn, optimizer):
for batch, (x, y) in enumerate(dataloader):
x, y = x.to(device), y.to(device)
pred = model(x)
loss = loss_fn(pred, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if batch % 100 == 0:
loss, current = loss.item(), batch * len(x)
print("loss = ", loss)
def test(dataloader, model, loss_fn):
size = len(dataloader.dataset)
num_batches = len(dataloader)
model.eval()
test_loss, correct = 0, 0
with torch.no_grad():
for x, y in dataloader:
x, y = x.to(device), y.to(device)
pred = model(x)
test_loss += loss_fn(pred, y).item()
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
test_loss /= num_batches
correct /= size
print("acc: ", correct)
epochs = 5
for t in range(epochs):
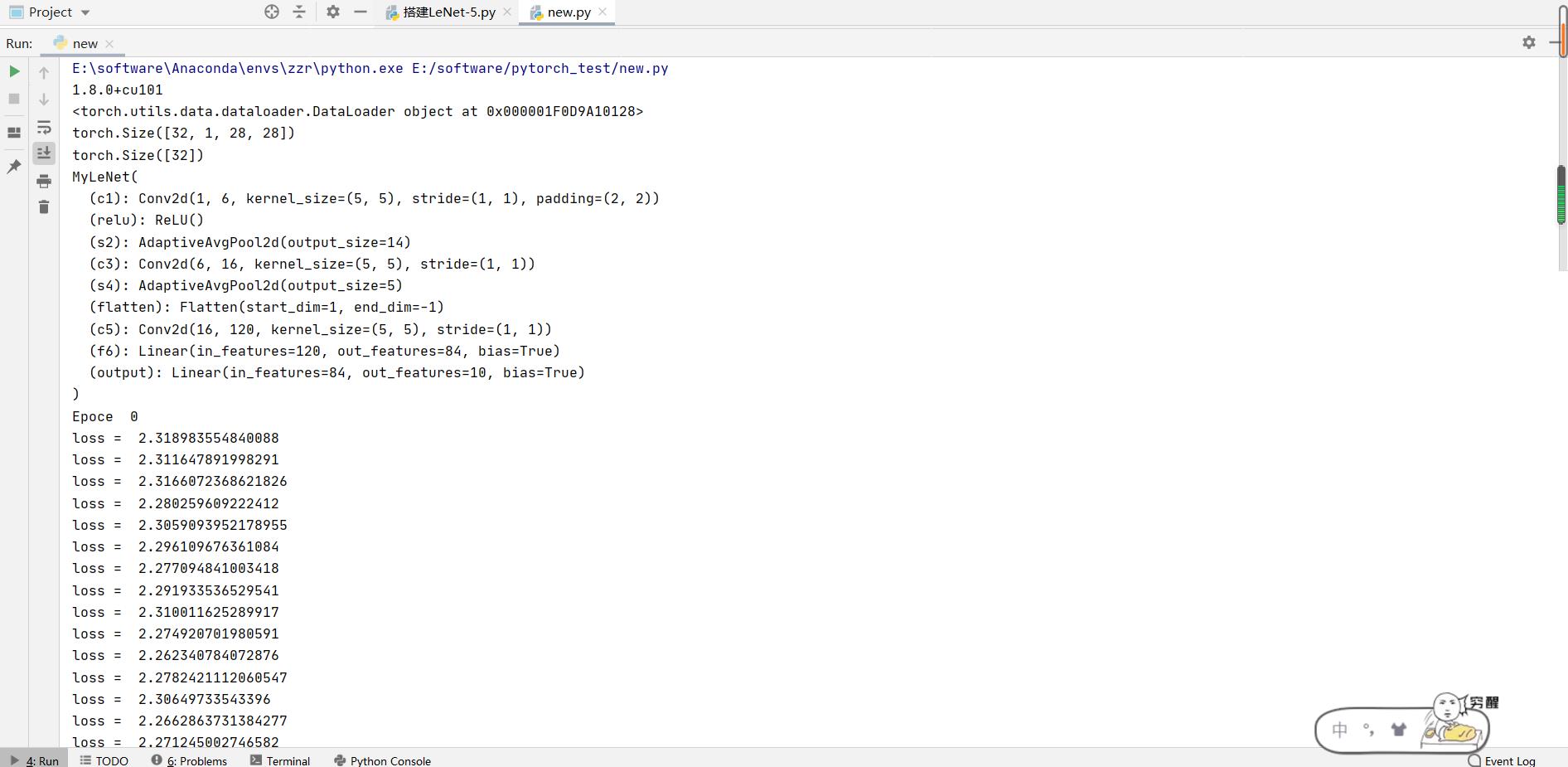
print("Epoce ", t)
train(train_dataloader, model, loss_fn, optimizer)
test(test_dataloader, model, loss_fn)
print("Done")
欢迎大家交流评论,一起学习
希望本文能帮助您解决您在这方面遇到的问题
感谢阅读
END
以上是关于「深度学习一遍过」必修8:搭建卷积神经网络 LeNet-5的主要内容,如果未能解决你的问题,请参考以下文章





