[Python系列-13]：人工智能 - 数学基础 -3- 数组元素的统计

Posted 2021-08-30 文火冰糖的硅基工坊

作者主页(文火冰糖的硅基工坊)：https://blog.csdn.net/HiWangWenBing

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/119298643

---

目录

第1章 概述

第2章 找极值

2.1 找最大值：mumpy.amax()

2.2 找最小值：numpy.amin() 

2.3 极值振幅：numpy.ptp()

第3章 百分位数统计：numpy.percentile()

第4章 数据序列的均值指标

4.1 概述

4.1 中值：numpy.median()

4.2 算术平均值：numpy.mean()

4.3 加权均值：numpy.average()

第6章 数据分布特征统计

6.1 概述

6.2 标准（方）差

6.2 样本方差：var（）

---

第1章 概述

NumPy 提供了很多统计函数，用于从数组中查找最小元素，最大元素，百分位标准差和方差等

https://www.runoob.com/numpy/numpy-linear-algebra.html

第2章 找极值

2.1 找最大值：mumpy.amax()

numpy.amax() 用于计算数组中的元素沿指定轴的最大值。

#实例
import numpy as np 
 
a = np.array([[3,7,5],[8,4,3],[2,4,9]])  
print ('我们的数组是：')
print (a)
print ('\\n')


print ('调用 amax() 函数：')
print (np.amax(a))                #整个矩阵扫描
print ('\\n')

print ('再次调用 amax() 函数：')
print (np.amax(a, axis =  0))     #按行扫描

输出结果为：

我们的数组是：
[[3 7 5]
 [8 4 3]
 [2 4 9]]



调用 amax() 函数：
9


再次调用 amax() 函数：
[8 7 9]

2.2 找最小值：numpy.amin() 

numpy.amin() 用于计算数组中的元素沿指定轴的最小值。

#实例
import numpy as np 
 
a = np.array([[3,7,5],[8,4,3],[2,4,9]])  
print ('我们的数组是：')
print (a)
print ('\\n')

print ('调用 amin() 函数：')
print (np.amin(a,1))              #按列扫描
print ('\\n')

print ('再次调用 amin() 函数：')
print (np.amin(a,0))              #按行扫描
print ('\\n')

输出结果为：

我们的数组是：
[[3 7 5]
 [8 4 3]
 [2 4 9]]


调用 amin() 函数：
[3 3 2]


再次调用 amin() 函数：
[2 4 3]

2.3 极值振幅：numpy.ptp()

numpy.ptp()函数计算数组中元素最大值与最小值的差（最大值 - 最小值）

#实例
import numpy as np 
 
a = np.array([[3,7,5],[8,4,3],[2,4,9]])  
print ('我们的数组是：')
print (a)
print ('\\n')

print ('调用 ptp() 函数：')
print (np.ptp(a))
print ('\\n')

print ('沿轴 1 调用 ptp() 函数：')
print (np.ptp(a, axis =  1))
print ('\\n')

print ('沿轴 0 调用 ptp() 函数：')
print (np.ptp(a, axis =  0))
print ('\\n')

#输出结果为：

我们的数组是：
[[3 7 5]
 [8 4 3]
 [2 4 9]]


调用 ptp() 函数：
7


沿轴 1 调用 ptp() 函数：
[4 5 7]


沿轴 0 调用 ptp() 函数：
[6 3 6]

第3章 百分位数统计：numpy.percentile()

百分位数是统计中使用的度量，表示小于这个值的观察值的百分比。

函数numpy.percentile()接受以下参数。

numpy.percentile(a, q, axis)

参数说明：

• a: 输入数组
• q: 要计算的百分位数，在 0 ~ 100 之间
• axis: 沿着它计算百分位数的轴

首先明确百分位数：

第 p 个百分位数是这样一个值，它使得至少有 p% 的数据项小于或等于这个值，且至少有 (100-p)% 的数据项大于或等于这个值。

举个例子：高等院校的入学考试成绩经常以百分位数的形式报告。比如，假设某个考生在入学考试中的语文部分的原始分数为 54 分。相对于参加同一考试的其他学生来说，他的成绩如何并不容易知道。但是如果原始分数54分恰好对应的是第70百分位数，我们就能知道大约70%的学生的考分比他低，而约30%的学生考分比他高。

这里的 p = 70。

#实例
import numpy as np 
 
a = np.array([[10, 7, 4], [3, 2, 1]])
print ('我们的数组是：')
print (a)
 
print ('调用 percentile() 函数：')
# 50% 的分位数，就是 a 里排序之后的中位数
print (np.percentile(a, 50)) 
 
# axis 为 0，在纵列上求
print (np.percentile(a, 50, axis=0)) 
 
# axis 为 1，在横行上求
print (np.percentile(a, 50, axis=1)) 
 
# 保持维度不变
print (np.percentile(a, 50, axis=1, keepdims=True))

#输出结果为：

我们的数组是：
[[10  7  4]
 [ 3  2  1]]
调用 percentile() 函数：
3.5
[6.5 4.5 2.5]
[7. 2.]
[[7.]
 [2.]]

第4章 数据序列的均值指标

4.1 概述

中位值不同于平均值。

4.1 中值：numpy.median()

numpy.median() 函数用于计算数组 a 中元素的中位数（中值）

中位数（Median）又称中值，统计学中的专有名词，是按顺序排列的一组数据中居于中间位置的数，代表一个样本、种群或概率分布中的一个数值，其可将数值集合划分为相等的上下两部分。

对于有限的数集，可以通过把所有观察值高低排序后找出正中间的一个作为中位数。

如果观察值有偶数个，通常取最中间的两个数值的平均数作为中位数。

如果观察值有奇数个，通常取最中间的一个数字作为中位数。

因此，中位数是由排序后的位置来决定的，与数值本身没有关系。

中值的前提是：排序。

#实例
import numpy as np 
 
a = np.array([[30,65,70],[80,95,10],[50,90,60]])  
print ('我们的数组是：')
print (a)
print ('\\n')
print ('调用 median() 函数：')
print (np.median(a))
print ('\\n')
print ('沿轴 0 调用 median() 函数：')
print (np.median(a, axis =  0))
print ('\\n')
print ('沿轴 1 调用 median() 函数：')
print (np.median(a, axis =  1))

#输出结果为：

我们的数组是：
[[30 65 70]
 [80 95 10]
 [50 90 60]]


调用 median() 函数：
65.0


沿轴 0 调用 median() 函数：
[50. 90. 60.]


沿轴 1 调用 median() 函数：
[65. 80. 60.]

4.2 算术平均值：numpy.mean()

（1）原理概述

算术平均值是沿轴的元素的总和除以元素的数量。

算术平均值平均的前提是：求出所有带符号数值的总和。

简单算术平均公式：

设一组数据为X1，X2，...，Xn，简单的算术平均数的计算公式为：

（2） 函数使用说明

numpy.mean() 函数返回数组中元素的算术平均值。 如果提供了轴，则沿其计算。

 （3）案例

#实例
import numpy as np 
 
a = np.array([[1,2,3],[3,4,5],[4,5,6]])  
print ('我们的数组是：')
print (a)
print ('\\n')

print ('调用 mean() 函数：')
print (np.mean(a))
print ('\\n')

print ('沿轴 0 调用 mean() 函数：')
print (np.mean(a, axis =  0))
print ('\\n')

print ('沿轴 1 调用 mean() 函数：')
print (np.mean(a, axis =  1))
print ('\\n')

#输出结果为：

我们的数组是：
[[1 2 3]
 [3 4 5]
 [4 5 6]]


调用 mean() 函数：
3.6666666666666665


沿轴 0 调用 mean() 函数：
[2.66666667 3.66666667 4.66666667]


沿轴 1 调用 mean() 函数：
[2. 4. 5.]

4.3 加权均值：numpy.average()

（1）原理概述

numpy.average() 函数根据在另一个数组中给出的各自的权重，来计算当前数组中元素的加权平均值。因此，这里有两个数组，一个是数值数组，一个是权重数组。

主要用于处理经分组整理的数据。

设原始数据为被分成K组，各组的组中的数值序列为X1，X2，...，Xk，各组的数值序列的频数（又称为权重）分别为f1，f2，...，fk，加权算术平均数的计算公式为：

（2）函数使用说明

该函数可以接受一个轴参数。 如果没有指定轴，则数组会被展开。

加权平均值即将各数值乘以相应的权数，然后加总求和得到总体值，再除以总的单位数。

如：考虑数组[1,2,3,4]和相应的权重[4,3,2,1]，通过将相应元素的乘积相加，并将和除以权重的和，来计算加权平均值：加权平均值 = (1*4+2*3+3*2+4*1)/(4+3+2+1)

（3）案例：

#实例
import numpy as np 
 
a = np.array([1,2,3,4])  
print ('我们的数组是：')
print (a)
print ('\\n')

print ('调用 average() 函数：')
print (np.average(a))
print ('\\n')

# 不指定权重时相当于 mean 函数
wts = np.array([4,3,2,1])  

print ('再次调用 average() 函数：')
print (np.average(a,weights = wts))
print ('\\n')

# 如果 returned 参数设为 true，则返回权重的和  
print ('权重的和：')
print (np.average([1,2,3,  4],weights =  [4,3,2,1], returned =  True))

输出结果为：

我们的数组是：
[1 2 3 4]


调用 average() 函数：
2.5


再次调用 average() 函数：
2.0


权重的和：
(2.0, 10.0)

第6章 数据分布特征统计

6.1 概述

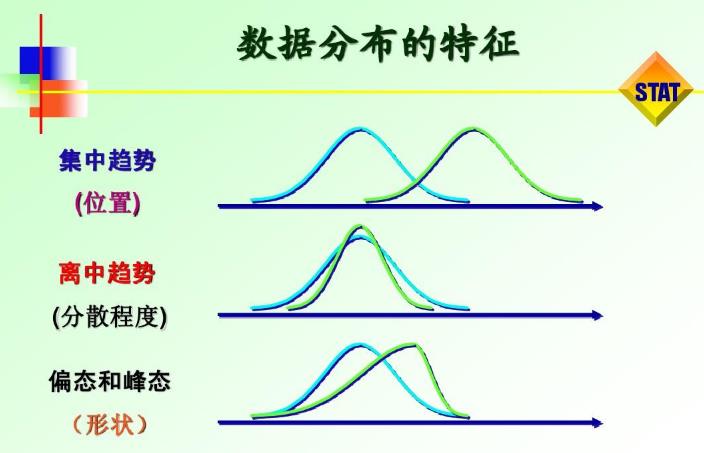
6.2 标准（方）差

（1）理论概述

标准差是一组数据离平均值的分散程度的一种度量。

标准差（Standard Deviation） ，是离均差平方的算术平均数（即：方差）的算术平方根，用σ表示。

标准差也被称为标准偏差，或者实验标准差，在概率统计中最常使用作为统计分布程度上的测量依据。

 

 在实验中单次测量总是难免会产生误差，为此我们经常测量多次，然后用测量值的平均值表示测量的量，并用误差条来表征数据的分布，其中误差条的高度为±标准误差。这里即标准差。

 

如果数组是 [1，2，3，4]，则其平均值为 2.5。 因此，差的平方是 [2.25,0.25,0.25,2.25]，并且再求其平均值的平方根除以 4，即 sqrt(5/4) ，结果为 1.1180339887498949。

#实例
import numpy as np 
 
print (np.std([1,2,3,4]))


输出结果为：

1.1180339887498949

6.2 样本方差：var（）

（1）概述

统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数，即 mean((x - x.mean())** 2)。 #mean：求平均

换句话说，标准差是方差的平方根

（2）方差与标准方差的关系：

备注：正态分布使用的是标准方差，而不是方差。

（3）实例

#实例
import numpy as np
 
print (np.var([1,2,3,4]))
输出结果为：

1.25

---

作者主页(文火冰糖的硅基工坊)：https://blog.csdn.net/HiWangWenBing

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/119298643