LeetCode 002 数组系列

Posted Al_tair

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了LeetCode 002 数组系列相关的知识，希望对你有一定的参考价值。

数组(二)

大家好！我是小笙！我们即将开始探索的是数组（二）系列的题型，刷题一开始刷起来感觉很难，但是一直刷题一直爽，我们可以从中享受到刷题的快乐！加油！

数组(二)系列题型如下

数组系列二

二维数组及滚动数组(661)

661题：图片平滑器

包含整数的二维矩阵 M 表示一个图片的灰度。你需要设计一个平滑器来让每一个单元的灰度成为平均灰度 (向下舍入)
，平均灰度的计算是周围的8个单元和它本身的值求平均，如果周围的单元格不足八个，则尽可能多的利用它们。
示例 1:
输入: [[1,1,1], [1,0,1], [1,1,1]] 输出: [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
解释: 对于点 (0,0), (0,2), (2,0), (2,2): 平均(3/4) = 平均(0.75) = 0 对于点 (0,1), (1,0), (1,2), (2,1): 平均(5/6) = 平均(0.83333333) = 0 对于点 (1,1): 平均(8/9) = 平均(0.88888889) = 0
注意:
给定矩阵中的整数范围为 [0, 255]。 矩阵的长和宽的范围均为 [1, 150]。

暴力解法（MyCode）

首先呢，先放上我的想法思路如下：if 就是 if,被官方解法的一句代码打破了！
我觉得需要注意的是如何获取二维数组的行与列
img.length 行 img[0].length 列

class Solution {
    public int[][] imageSmoother(int[][] img) {
        int sum,count=1;
        int [][]Reimg = new int[img.length][img[0].length];
        for(int i=0;i<img.length;i++){
            for(int j=0;j<img[0].length;j++){
                sum = img[i][j];
                if(j > 0){
                    sum = sum+img[i][j-1];
                    count++;
                }
                if(i > 0){
                    sum = sum+img[i-1][j];
                    count++;
                }
                if(j < img[0].length-1){
                    sum = sum+img[i][j+1];
                    count++;
                }
                if(i < img.length-1){
                    sum = sum+img[i+1][j];
                    count++;
                }
                if(j > 0 && i > 0){
                    sum = sum+img[i-1][j-1];
                    count++;
                }
                if(j > 0 && i < img.length-1){
                    sum = sum+img[i+1][j-1];
                    count++;
                }
                if(j < img[0].length-1 && i > 0){
                    sum = sum+img[i-1][j+1];
                    count++;
                }
                if(j < img[0].length-1 && i < img.length-1){
                    sum = sum+img[i+1][j+1];
                    count++;
                }
                sum = sum/count;
                Reimg[i][j] = sum;
                count = 1;
            }
        }
        return Reimg;
    }
}

执行用时：8 ms, 在所有 Java 提交中击败了70.23%的用户
内存消耗：39.4 MB, 在所有 Java 提交中击败了56.86%的用户

暴力解法官方（Other’s Code）

官方写出的思路和我是一致，但是值得我去学习就是他的书写规范和简洁，让人耳目一新！原来还可以这么简洁！

class Solution {
    public int[][] imageSmoother(int[][] M) {
        int R = M.length, C = M[0].length;
        int[][] ans = new int[R][C];

        for (int r = 0; r < R; ++r)
            for (int c = 0; c < C; ++c) {
                int count = 0;
                for (int nr = r-1; nr <= r+1; ++nr)
                    for (int nc = c-1; nc <= c+1; ++nc) {
                        if (0 <= nr && nr < R && 0 <= nc && nc < C) {
                            ans[r][c] += M[nr][nc];
                            count++;
                        }
                    }
                ans[r][c] /= count;
            }
        return ans;
    }
}

数组的旋转(189）

189题：旋转数组

给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。
进阶： 尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。 你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗？
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步:[7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]
示例2:
输入：nums = [-1,-100,3,99], k = 2 输出：[3,99,-1,-100]
解释:
向右旋转 1 步:[99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]

提示：
1 <= nums.length <= 2 * 104
-231 <= nums[i] <= 231 - 1
0 <= k <= 105

方法一：使用额外的数组(Other’s Code)

这种解法不符合题目的要求
这个解法亮点：newArr[(i + k) % n] = nums[i];
复杂度分析

  • 时间复杂度： O(n)O(n)，其中 nn 为数组的长度。
  • 空间复杂度： O(n)O(n)。
class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        int[] newArr = new int[n];
        for (int i = 0; i < n; ++i) {
            newArr[(i + k) % n] = nums[i];
        }
        System.arraycopy(newArr, 0, nums, 0, n);
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了66.92%的用户
内存消耗：55.2 MB, 在所有 Java 提交中击败了61.18%的用户

方法二：暴力解法(MyCode)

这种解法的坏处就是运行时间特别久，达到了题目的要求

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length,temp;
        k = k % n;
        while(k>0){
            temp = nums[nums.length-1];
            for(int i=nums.length-1;i>0;i--){
                nums[i] = nums[i-1];
            }
            nums[0] = temp;
            k--;
        }
    }
}

方法三：数组翻转（Other’s Code）

这个是官方解法

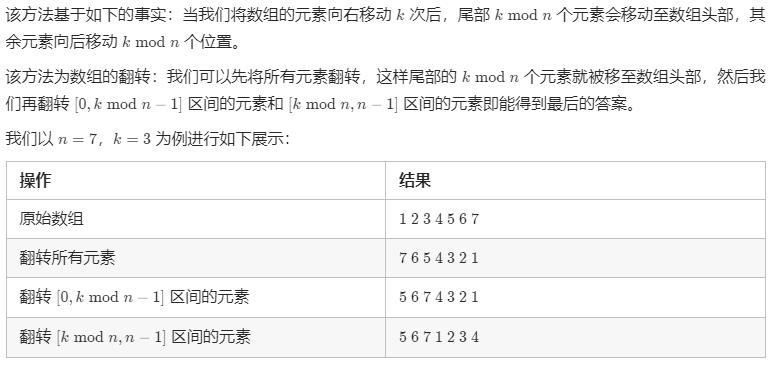
class Solution {
    public void rotate(int[] nums, int k) {
        k %= nums.length;
        reverse(nums, 0, nums.length - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.length - 1);
    }

    public void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            start += 1;
            end -= 1;
        }
    }
}

特定顺序遍历二维数组(54）

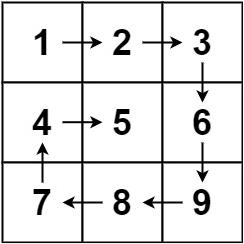
54题：螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。
示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]
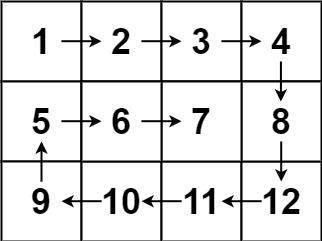
示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

方法一：限幅（MyCode）

我做这个题目的时候最开始的想法就是数组最终都会往所谓的中心靠拢类似今年“烟花”台风，就想给它四个边界，最终慢慢减少到一个点就是结束点
算法逻辑：
顺序无非就是右下左上四个步骤
我们在进行完每一个步骤的时候将边界往里面收一格，最终就是实现了
具体步骤看代码

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        // flag标志位用来表示上下左右的次序 右 1  下 2  左 3  上 4
        int up=0,down=matrix.length-1,left=0,right=matrix[0].length-1,flag=1;
        List<Integer> list = new ArrayList<>();
        while(up != down || left != right){
            if(flag == 1){
                for(int i=left;i<=right;i++){
                    list.add(matrix[up][i]);
                }
                if(up != down || left != right){
                    up++;
                }
            }else if(flag == 2){
                for(int i=up;i<=down;i++){
                    list.add(matrix[i][right]);
                }
                if(up != down || left != right){
                    right--;
                }
            }else if(flag == 3){
                for(int i=right;i>=left;i--){
                    list.add(matrix[down][i]);
                }
                if(up != down || left != right){
                    down--;
                }
            }else if(flag == 4){
                for(int i=down;i>=up;i--){
                    list.add(matrix[i][left]);
                }
                if(up != down || left != right){
                    left++;
                }
            }

            // 限幅
            flag++;
            if(flag == 5){
                flag = 1;
            }
        }
        list.add(matrix[up][left]);
        return list;
    }
}

方法二：模拟（Other’s Code）

可以模拟螺旋矩阵的路径。初始位置是矩阵的左上角，初始方向是向右，当路径超出界限或者进入之前访问过的位置时，顺时针旋转，进入下一个方向。判断路径是否进入之前访问过的位置需要使用一个与输入矩阵大小相同的辅助矩阵visited，其中的每个元素表示该位置是否被访问过。当一个元素被访问时，将visited 中的对应位置的元素设为已访问。
如何判断路径是否结束？由于矩阵中的每个元素都被访问一次，因此路径的长度即为矩阵中的元素数量，当路径的长度达到矩阵中的元素数量时即为完整路径，将该路径返回。

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return order;
        }
        int rows = matrix.length, columns = matrix[0].length;
        boolean[][] visited = new boolean[rows][columns];
        int total = rows * columns;
        int row = 0, column = 0;
        int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        int directionIndex = 0;
        for (int i = 0; i < total; i++) {
            order.add(matrix[row][column]);
            visited[row][column] = true;
            int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];
            if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {
                directionIndex = (directionIndex + 1) % 4;
            }
            row += directions[directionIndex][0];
            column += directions[directionIndex][1];
        }
        return order;
    }
}

方法三：按层模拟（Other’s Code）

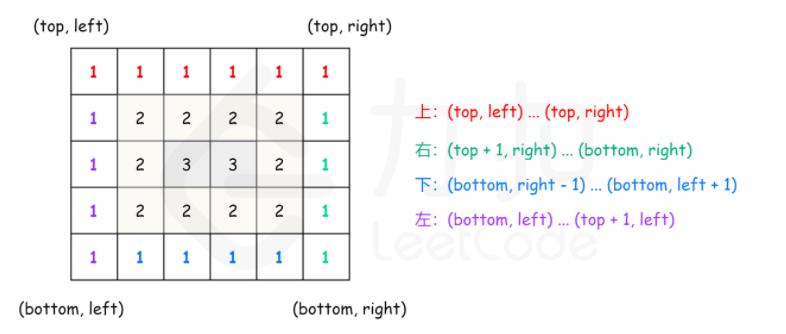
如图所示，我们每次循环的目的就是自外向内一步一步深入
从1->2->3->…->end
could you understand me?

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
		// 排除无参数传入
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return order;
        }
        int rows = matrix.length, columns = matrix[0].length;
        int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
        
        while (left <= right && top <= bottom) {
        	// 最上面的行添加
            for (int column = left; column <= right; column++) {
                order.add(matrix[top][column]);
            }
            // 最右边的添加
            for (int row = top + 1; row <= bottom; row++) {
                order.add(matrix[row][right]);
            }
            // 排除当二行二列的数组
            if (left < right && top < bottom) {
            	// 最下边的添加
                for (以上是关于LeetCode 002 数组系列的主要内容，如果未能解决你的问题，请参考以下文章
 

 5-002-(LeetCode- 33) 搜索旋转排序数组


 Leetcode.1024 视频拼接


 002addTwoNumbers


 002LeetCode--TwoNumbers


 LeetCode810. 黑板异或游戏/455. 分发饼干/剑指Offer 53 - I. 在排序数组中查找数字 I/53 - II. 0～n-1中缺失的数字/54. 二叉搜索树的第k大节点(代码片段


 817. Linked List Components - LeetCode