FTT从入门到自闭

Posted 2021-08-29 Harris-H

FTT从入门到自闭

0.基本定义

FFT全称(Fast Fourier Transformation)

中文名：快速傅里叶离散变换

作用是能以$O(nlogn)$　计算多项式乘法。

$n$​次多项式：$F(x)=ax^n+bx{n-1}+cx^{n-2}\\dots $

$F[i]$​ 表示$F(x)$的$i$次项系数。​

$F(x)=\sum _{i=0}^{n}F[i]x^i$​

---

乘法的本质(卷积)

两个$n$次多项式$A(x),B(x)$相乘。

$C=A\ast B$

$C[k]=\sum _{i=0}^{k}A[i]B[k-i]=\sum _{i+j=k}A[i]B[j]$​

因此乘法的本质就是加法卷积。

---

暴力卷积

P3803 【模板】多项式乘法（FFT）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+5;
int n,m;
ll a[N],b[N],c[N];
void mul(ll *a,ll *b,ll *c){
	for(int k=0;k<=n+m;k++)
		for(int i=0;i<=k;i++)
			c[k]+=a[i]*b[k-i];
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=0;i<=n;i++) scanf("%lld",&a[i]);
	for(int i=0;i<=m;i++) scanf("%lld",&b[i]);
	mul(a,b,c);
	for(int i=0;i<=n+m;i++) printf("%lld ",c[i]);printf("\\n");
	return 0;
}

1.DFT&IDFT

用$n+1$​个点值(有序数对) 可以唯一确定一个$n$次多项式。

因此便有了$FFT$的算法流程：

把系数表达转换为点值表达$\Rightarrow$ 点值表达相乘 $\Rightarrow$ 点值表达转换为系数表达。

把系数表达转换为点值表达”的算法叫做DFT

把点值表达转换为系数表达”的算法叫做IDFT(DFT的逆运算)

• 从一个多项式的系数表达确定其点值表达的过程称为求值(毕竟求点值表达的过程就是取了 n 个 x 然后扔进了多项式求了 n 个值出来);
• 而求值运算的逆运算(也就是从一个多项式的点值表达确定其系数表达)被称为插值.

总结

在平面直角坐标系中,给你(n+1)个点就能确定一个n次多项式(函数)。

点值表示相乘(点乘)远快于暴力卷积。

---

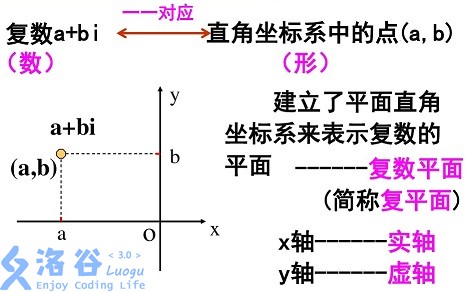
2.单位根(复数)及其性质

关于复数

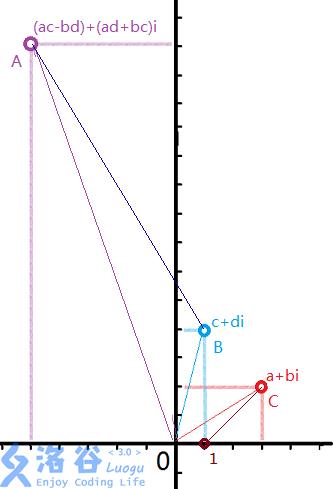
复数相乘时,模长相乘,幅角相加！

---

单位根

看起来很高大上,这是傅里叶快速变换的重要内容。

• n次单位根(n为正整数)是n次幂为1的复数。

换句话说,就是方程$x^n=1$的复数解。

---

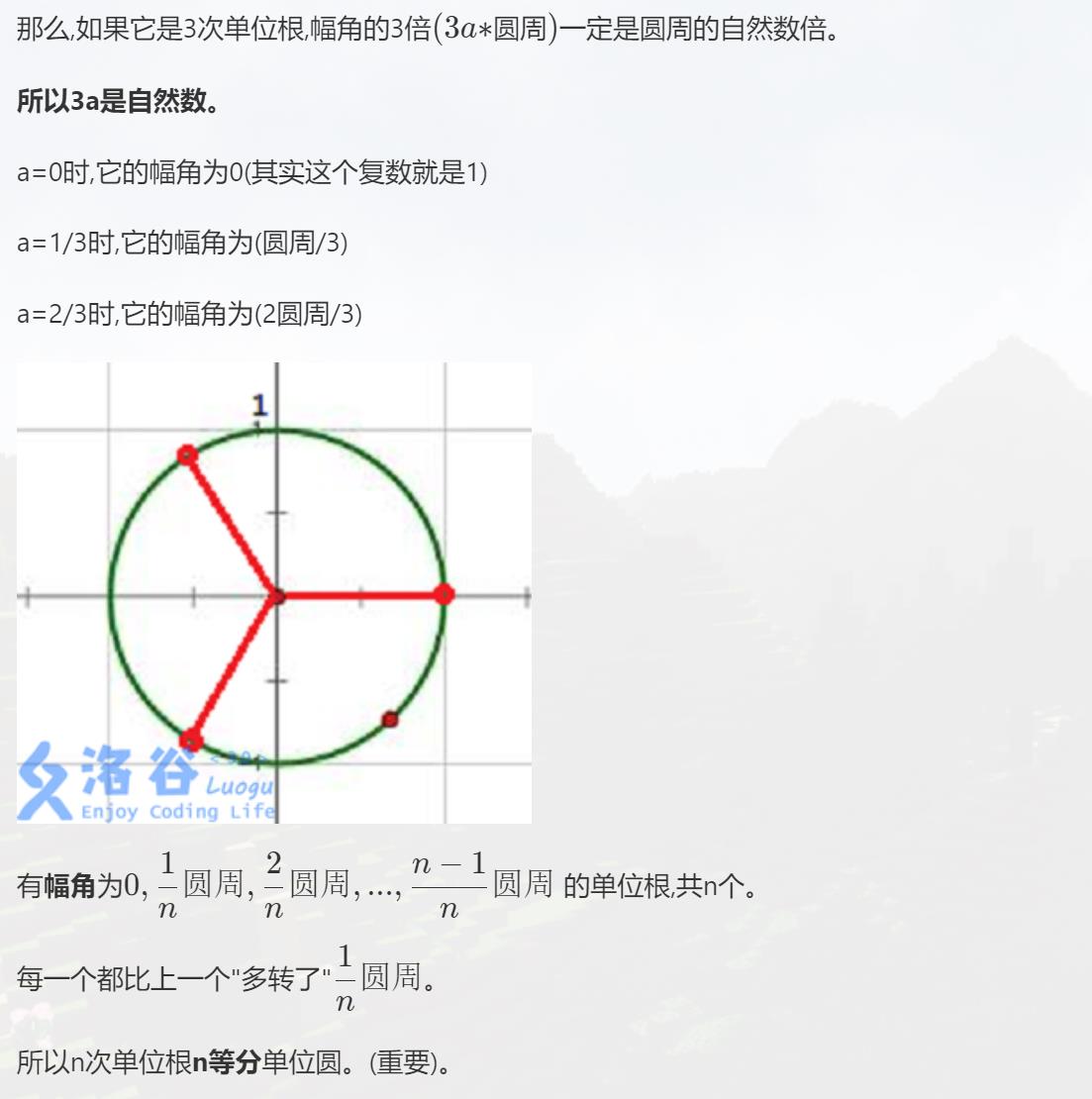
单位根的性质

• ${\omega }_n^0=1$
• ${\omega }_n^k=({\omega }_n^1{)}^k$
• ${\omega }_n^j\ast {\omega }_n^k={\omega }_n^{j+k}$
• ${\omega }_{2n}^{2k}={\omega }_n^k$
• 若$n$为偶数，${\omega }_n^{k+n/2}=-{\omega }_n^k$​

总结

复数把数轴扩展到了复平面上,复数可以对应复平面上一个点。

复数也有四则运算。复数相乘时,模长相乘,幅角相加。

n次单位根(n为正整数)是n次幂为1的复数。

把单位根画到单位圆上之后,就能整出一些性质。

---

3.DFT的加速版本

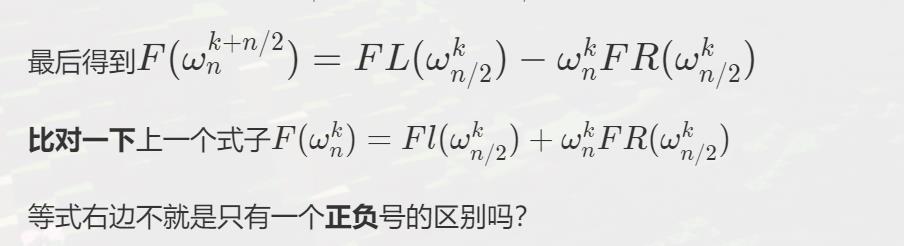
$F(w_n^k)=FL(w_{n/2}^k)+w_n^{k}FR(w_{n/2}^k)$

$F(w_n^{k+n/2})=FL(w_{n/2}^k)-w_n^{k}FR(w_{n/2}^k)$​

---

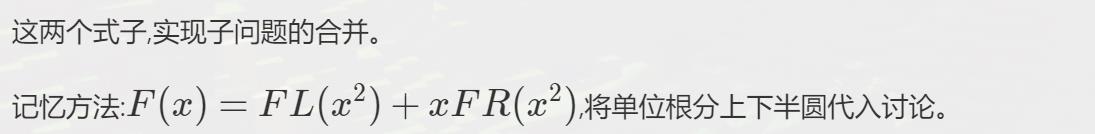
4.DFT的代码实现

还有一个小细节。

上文有一句话：“保证n是2的整幂,不会出现分得不均匀的情况。”

实际应用中,$n$不一定是$2$的正整数次幂。

我们可以补项,在最高次强行添加一些系数为0的项(类似于高精度补0)。不影响我们的计算结果,却占了位置。(具体见代码)

讲完了这些我们可以开始写$DFT$了

1.复数结构体

#include <iostream>
using namespace std;
struct CP
{
  CP (double xx=0,double yy=0){x=xx,y=yy;}
  double x,y;
  CP operator + (CP const &B) const
  {return CP(x+B.x,y+B.y);}
  CP operator - (CP const &B) const
  {return CP(x-B.x,y-B.y);}
  CP operator * (CP const &B) const
  {return CP(x*B.x-y*B.y,x*B.y+y*B.x);}
  CP operator / (CP const &B) const {
    double t=B.x*B.x+B.y*B.y;
    return CP((x*B.x+y*B.y)/t,
              (y以上是关于FTT从入门到自闭的主要内容，如果未能解决你的问题，请参考以下文章
 
 从入门到自闭之Python--Redis
 从入门到自闭之Python--虚拟环境如何安装
 从入门到自闭之Python--MySQL数据库安装
 从入门到自闭之--网络编程
 从入门到自闭之Python--MySQL数据库的操作命令
 从入门到自闭之Python--MySQL数据库的单表操作