堆和优先级队列2:java实现堆和优先级队列
Posted 纵横千里,捭阖四方
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了堆和优先级队列2:java实现堆和优先级队列相关的知识,希望对你有一定的参考价值。
1.什么是优先级队列
在C++和java等库中,都提供了优先级队列这个容器,java中的优先级队列是PriorityQueue。其实底层就是一个堆的结构,只不过将堆封装了一层而已。其实名字叫个优先级队列,但总觉得和队列是不沾边的。 不知道为啥这么叫。
接下来我们看一下java实现堆和使用优先级队列的一些代码,这些面试一般不用写,我们感受一下其实现原理就好。
PriorityQueue的实现直接参考jdk源码。我们这里用java自己实现一个。
2.堆的建立过程
给定一个初始化数组来建立一个最大堆,假定数组长度为N,则从N/2到1位置处,对于每一个节点元素进行向下调整,则最终数组为一个最大堆。
public MaxPQ(Key[] keys){
n = keys.length;
pq = (Key[]) new Object[n+1];
for(int i=0; i<n; i++){
pq[i+1] = keys[i];
}
for(int k=n/2; k>=1; k--){
sink(k);
}
}插入操作
首先判断当前元素数量与堆容量大小关系,判断是否需要扩容;如果不需要,则将新插入元素放置到数组最后位置。将最后位置元素执行向上调整操作,可以实现堆的平衡。
public void insert(Key x){
if(n==pq.length-1) resize(2*pq.length);
pq[++n] = x;
swim(n);
}
private void resize(int capacity) {
Key[] tmp = (Key[]) new Object[capacity];
for(int i=1; i<=n; i++){
tmp[i] = pq[i];
}
pq = tmp;
}删除最大值
最大堆可以在O(1)内返回数组元素的最大值,在O(logN)内删除最大值并且调整堆有序。
删除最大值,即删除索引位置为1的元素,在此首先记录堆顶元素值,然后将数组最后一个元素与堆顶元素交换,对于堆顶新元素执行向下调整操作,以此保证堆有序。
public Key delMax(){
if(isEmpty()) return null;
Key max = pq[1];
exch(1, n--);
sink(1);
pq[n+1] = null;
if(n>0 && n==(pq.length-1)/4)
resize(pq.length/2);
return max;
}3.堆的调整算法
上一篇我们通过一个demo演示了调整完全二叉树为堆的方法,其实堆的调整有向上和向下两种方式。
3.1 向上调整
向上调整:以最大堆为例,如果某一个节点值小于其父节点,则需要交换该节点与父节点值,继续比较交换,直到根节点一直是有序的。
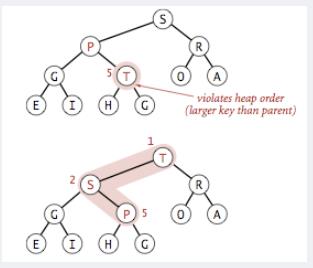
代码如下:
private void swim(int k) {
while(k>1 && less(k/2, k)){
exch(k, k/2);
k = k /2;
}
}其中less是小于判断,exch为交换操作
private void exch(int i, int j) {
Key swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
}
private boolean less(int i, int j) {
if(comparator==null){
return ((Comparable<Key>)pq[i]).compareTo((Key)pq[j])<0;
}else{
return comparator.compare(pq[i], pq[j])<0;
}
}3.2向下调整
最大堆,当某一个节点小于其左右孩子节点时,应该将该节点与左右孩子最大值节点交换,然后继续判断被交换孩子节点位置是否满足最大堆的定义。
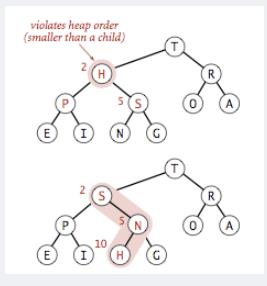
代码如下:
private void sink(int k) {
while(2*k<=n){
int j=2*k;
if(j<n && less(j, j+1)) j++;
if(!less(k, j)) break;
exch(k, j);
k = j;
}
}4.最终用最大堆实现的优先级队列
public class MaxPQ<Key> implements Iterable<Key>{
private Key[] pq;
private int n;
private Comparator<Key> comparator;
public MaxPQ(int initCapacity){
pq = (Key[]) new Object[initCapacity+1];
n = 0;
}
public MaxPQ(){
this(1);
}
public MaxPQ(int initCapacity, Comparator<Key> comparator){
this(initCapacity);
this.comparator = comparator;
}
public MaxPQ(Comparator<Key> comparator){
this(1, comparator);
}
public MaxPQ(Key[] keys){
n = keys.length;
pq = (Key[]) new Object[n+1];
for(int i=0; i<n; i++){
pq[i+1] = keys[i];
}
for(int k=n/2; k>=1; k--){
sink(k);
}
}
public void insert(Key x){
if(n==pq.length-1) resize(2*pq.length);
pq[++n] = x;
swim(n);
}
public Key delMax(){
if(isEmpty()) return null;
Key max = pq[1];
exch(1, n--);
sink(1);
pq[n+1] = null;
if(n>0 && n==(pq.length-1)/4)
resize(pq.length/2);
return max;
}
// is pq[1..N] a max heap?
private boolean isMaxHeap() {
return isMaxHeap(1);
}
// is subtree of pq[1..n] rooted at k a max heap?
private boolean isMaxHeap(int k) {
if (k > n) return true;
int left = 2*k;
int right = 2*k + 1;
if (left <= n && less(k, left)) return false;
if (right <= n && less(k, right)) return false;
return isMaxHeap(left) && isMaxHeap(right);
}
private boolean isEmpty() {
return n == 0;
}
private void swim(int k) {
while(k>1 && less(k/2, k)){
exch(k, k/2);
k = k /2;
}
}
private void resize(int capacity) {
Key[] tmp = (Key[]) new Object[capacity];
for(int i=1; i<=n; i++){
tmp[i] = pq[i];
}
pq = tmp;
}
private void sink(int k) {
while(2*k<=n){
int j=2*k;
if(j<n && less(j, j+1)) j++;
if(!less(k, j)) break;
exch(k, j);
k = j;
}
}
private void exch(int i, int j) {
Key swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
}
private boolean less(int i, int j) {
if(comparator==null){
return ((Comparable<Key>)pq[i]).compareTo((Key)pq[j])<0;
}else{
return comparator.compare(pq[i], pq[j])<0;
}
}
public int size() {
return n;
}
@Override
public Iterator<Key> iterator() {
return new HeapIterator();
}
//迭代访问首先将原堆数据复制一份,然后执行迭代访问
private class HeapIterator implements Iterator<Key> {
// create a new pq
private MaxPQ<Key> copy;
// add all items to copy of heap
// takes linear time since already in heap order so no keys move
public HeapIterator() {
if (comparator == null) copy = new MaxPQ<Key>(size());
else copy = new MaxPQ<Key>(size(), comparator);
for (int i = 1; i <= n; i++)
copy.insert(pq[i]);
}
public boolean hasNext() { return !copy.isEmpty(); }
public void remove() { throw new UnsupportedOperationException(); }
public Key next() {
if (!hasNext()) throw new NoSuchElementException();
return copy.delMax();
}
}
}以上内容摘自https://blog.csdn.net/u014106644/article/details/92764446
5.java中的PriorityQueue
在Java中也实现了自己的优先队列java.util.PriorityQueue,与我们自己写的不同之处在于,Java中内置的为最小堆,然后就是一些函数名不一样,底层还是维护了一个Object类型的数组,大家可以戳戳看有什么不同,另外如果想要把最小堆变成最大堆可以给PriorityQueue传入自己的比较器,例如:
// 默认为最小堆
PriorityQueue<Integer> pq = new PriorityQueue<>();
pq.add(5);
pq.add(2);
pq.add(1);
pq.add(10);
pq.add(3);
while (!pq.isEmpty()) {
System.out.println(pq.poll() + ", ");
}
System.out.println();
System.out.println("————————————————————————");
// 使用Lambda表达式传入自己的比较器转换成最大堆
PriorityQueue<Integer> pq2 = new PriorityQueue<>((a, b) -> b - a);
pq2.add(5);
pq2.add(2);
pq2.add(1);
pq2.add(10);
pq2.add(3);
while (!pq2.isEmpty()) {
System.out.println(pq2.poll() + ", ");
}以上是关于堆和优先级队列2:java实现堆和优先级队列的主要内容,如果未能解决你的问题,请参考以下文章