优于线性时间复杂度获取完全二叉树的结点数

Posted 2021-08-29 叶孤城_

目录

• • 问题描述
  • 概念介绍
  • 算法
  • 代码
  • 复杂度

问题描述

给你一个指向完全二叉树的根节点的指针，返回这棵树的总结点数，要求时间复杂度小于O(n)。

概念介绍

二叉树：

n（n≥0）个节点的有限集，它或为空树（n=0），或由一个根节点和两颗分别称为左子树和右子树的互不相交的二叉树构成

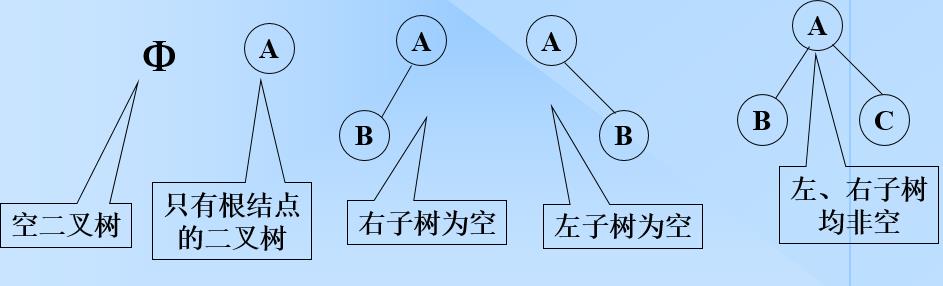
下面介绍两种特殊形式的二叉树

满二叉树

一颗深度为 k 且有 $2^k$ - 1 个结点的二叉树称为满二叉树，其特点是每一层上的结点数都是最大结点数。

完全二叉树

深度为 k，有 n 个结点的二叉树当且仅当其每一个结点都与深度为 k 的满二叉树中编号从 1 至 n 的结点一一对应时，称为完全二叉树。
其特点是：

1. 叶子结点只可能在层次最大的两层上出现
2. 对任一结点，若其右分支下子孙的最大层次为L，则其左分支下子孙的最大层次必为 L 或 L+1

算法

首先我们要知道：

1. 深度为 k 的满二叉树含有 $2^k$ - 1 个结点
2. 对于一颗完全二叉树，其左右子树至少有一颗为满二叉树

递归地来看，对每一个结点：

1 . 获取它的左子树的高度和右子树的高度
2 . 若高度相同，则左子树必为满二叉树，如下图一，直接计算得到其结点数，递归计算右子树（完全二叉树）的结点数
3 . 若高度不同，则右子树必为满二叉树，如下图二，直接计算得到其结点数，递归计算左子树（完全二叉树）的结点数

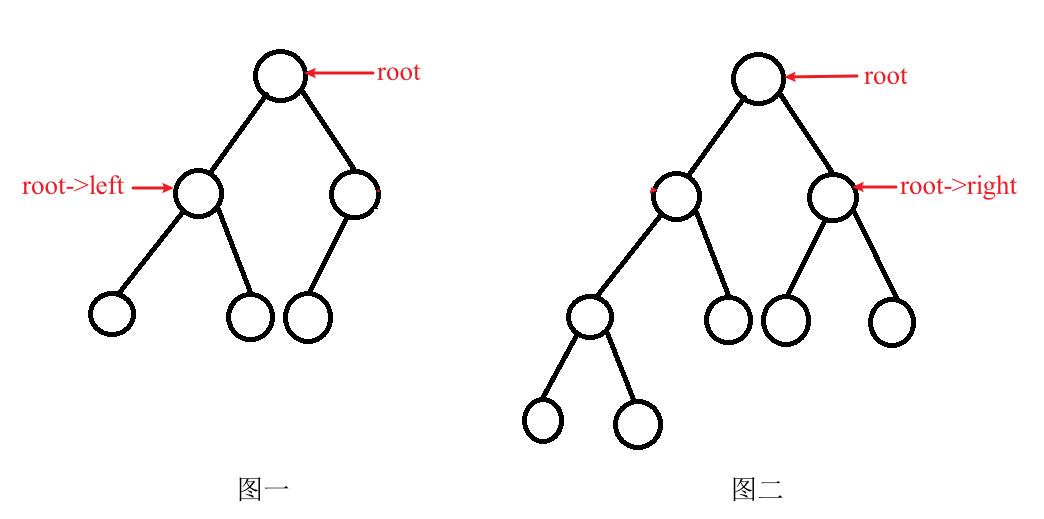
代码

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
	// 获取完全二叉树的深度
    int getTreeHeight(TreeNode* root){
        if(!root) return 0;
        return 1+getTreeHeight(root->left);
    }
    int dfs(TreeNode* root){
        if(!root) return 0;
        int leftHeight=getTreeHeight(root->left);
        int rightHeight=getTreeHeight(root->right);
        if(leftHeight==rightHeight)
            return 1+pow(2,leftHeight)-1+dfs(root->right);
        else
            return 1+dfs(root->left)+pow(2,rightHeight)-1;
    }
    int countNodes(TreeNode* root) {
        return dfs(root);
    }
};

复杂度

令数的高度为 h，在第1层，操作为获取左右子树的高度，这个过程需要 2*(h-1)次访问，在第二层，需要 2*(h-2)次访问，依次递推，则
O(N) = O( $2\ast (h-1+h-2+h-3+...+2+1)$ )
=O( $2\ast [(h-1)\ast h/2]$ )
=O( $h\ast h$ - h )
=O( $h^2$ )
=O( $(logN{)}^2$ )