[BPnet识别MNIST04]神经网络的变量和公式分析

Posted 2021-08-29 AIplusX

写在前面

今天正式进入前馈神经网络的公式推导环节，综合数据处理难度和公式推导难度以及神经网络的易理解性，我将之前放出的神经网络做了一些调整，之后给出。那么这篇文章主要进行神经网络的变量讲解，以及公式分析。

正文

主要内容在我的古月居博客：
[BPnet识别MNIST04]神经网络的变量和公式分析

神经网络图

神经网络图如下所示：

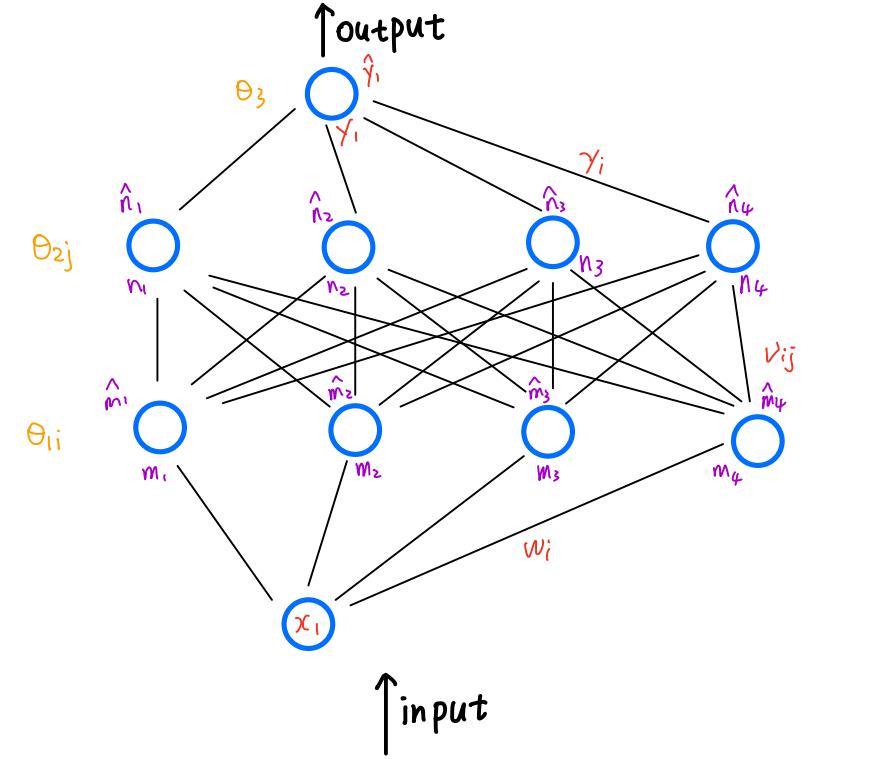
变量和公式分析

在神经网络中主要有这几个参数：

${\hat{y}}_1，y_1，{\gamma }_1，{\upsilon }_{11}，{\omega }_1，{\theta }_{11}，x_1，{\hat{n}}_1，{\hat{m}}_1，n_1，m_1，E_k$

让我来按顺序进行介绍：

${\hat{y}}_1$：是神经网络的最终计算输出；
$y_1$：图像的标签；
${\gamma }_1$：第二个隐层到输出层的权重；
${\upsilon }_{11}$：第一个隐层到第二个隐层的权重；
${\omega }_1$：输入层到第一个隐层的权重；
${\theta }_{11}$：第一个隐层的阈值；
$x_1$：输入层数据；
${\hat{n}}_1$：第二个隐层神经元的输出；
${\hat{m}}_1$：第一个隐层神经元的输出；
$n_1$：第二个隐层神经元的输入；
$m_1$：第一个隐层神经元的输入；
$E_k$：均方误差函数。

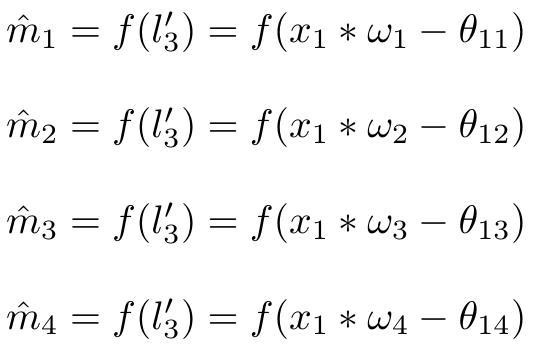
从第一个隐层到第二个隐层的公式：

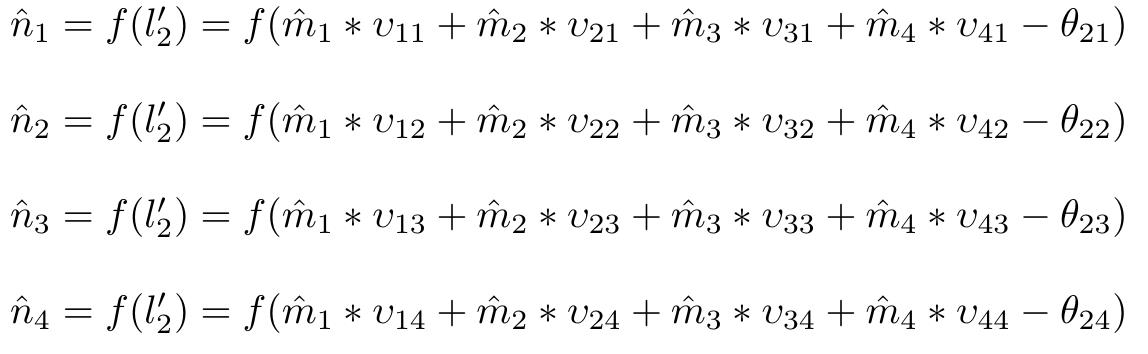
从第二个隐层到输出层的公式：

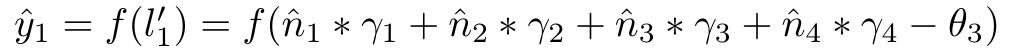
写出了各层的公式之后就可以进行梯度下降的公式推导啦，明天更新~

latex公式源码：

\\documentclass{article} 
\\title{AIplusX} 
\\author{AIplusX} 
\\begin{document} 
	\\ 
	\\\\$ \\hat{y}_{1} = f(l_{1}') = f(\\hat{n}_{1} * \\gamma_{1} + \\hat{n}_{2} * \\gamma_{2} +
	\\hat{n}_{3} * \\gamma_{3} +\\hat{n}_{4} * \\gamma_{4} - \\theta_{3}) $
	\\\\
	\\\\ $ \\hat{n}_{1} = f(l_{2}')= f(\\hat{m}_{1} * \\upsilon_{11} + \\hat{m}_{2} * \\upsilon_{21} +
	\\hat{m}_{3} * \\upsilon_{31} +\\hat{m}_{4} * \\upsilon_{41} - \\theta_{21}) $
	\\\\
	\\\\$ \\hat{n}_{2} = f(l_{2}')= f(\\hat{m}_{1} * \\upsilon_{12} + \\hat{m}_{2} * \\upsilon_{22} +
	\\hat{m}_{3} * \\upsilon_{32} +\\hat{m}_{4} * \\upsilon_{42} - \\theta_{22}) $
		\\\\
	\\\\$ \\hat{n}_{3} = f(l_{2}')= f(\\hat{m}_{1} * \\upsilon_{13} + \\hat{m}_{2} * \\upsilon_{23} +
	\\hat{m}_{3} * \\upsilon_{33} +\\hat{m}_{4} * \\upsilon_{43} - \\theta_{23}) $
		\\\\
	\\\\$ \\hat{n}_{4} = f(l_{2}')= f(\\hat{m}_{1} * \\upsilon_{14} + \\hat{m}_{2} * \\upsilon_{24} +
	\\hat{m}_{3} * \\upsilon_{34} +\\hat{m}_{4} * \\upsilon_{44} - \\theta_{24}) $
	\\\\
	\\\\$ \\hat{m}_{1} = f(l_{3}')= f(x_{1} * \\omega_{1} - \\theta_{11}) $
	\\\\
	\\\\$ \\hat{m}_{2} = f(l_{3}')= f(x_{1} * \\omega_{2} - \\theta_{12}) $
	\\\\
	\\\\$ \\hat{m}_{3} = f(l_{3}')= f(x_{1} * \\omega_{3} - \\theta_{13}) $
	\\\\
	\\\\$ \\hat{m}_{4} = f(l_{3}')= f(x_{1} * \\omega_{4} - \\theta_{14}) $
	\\\\
	\\\\$E_{k} = \\frac{1}{2} * ( \\hat{y}_{1} - y)^{2}$
	\\\\
	\\\\$ \\frac{\\partial E_{k}}{\\partial \\upsilon_{11}} = \\frac{\\partial E_{k}}{\\partial \\hat{y}_{1}} *
		\\frac{\\partial \\hat{y}_{1}}{\\partial \\hat{n}_{1}} * \\frac{\\partial \\hat{n}_{1}}{\\partial \\upsilon_{11}} + 
		\\frac{\\partial E_{k}}{\\partial \\hat{y}_{2}} *
		\\frac{\\partial \\hat{y}_{2}}{\\partial \\hat{n}_{2}} * \\frac{\\partial \\hat{n}_{2}}{\\partial \\upsilon_{11}} + 
		\\frac{\\partial E_{k}}{\\partial \\hat{y}_{3}} *
		\\frac{\\partial \\hat{y}_{3}}{\\partial \\hat{n}_{3}} * \\frac{\\partial \\hat{n}_{3}}{\\partial \\upsilon_{11}} + 
		\\frac{\\partial E_{k}}{\\partial \\hat{y}_{4}} *
		\\frac{\\partial \\hat{y}_{4}}{\\partial \\hat{n}_{4}} * \\frac{\\partial \\hat{n}_{4}}{\\partial \\upsilon_{11}}  
		$

\\end{document}

正文

主要内容在我的古月居博客：
[BPnet识别MNIST04]神经网络的变量和公式分析