python库整理:networkx 包
Posted 刘文巾
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了python库整理:networkx 包相关的知识,希望对你有一定的参考价值。
1 创建图形
创建一个没有节点和边的空图形。
import networkx as nx
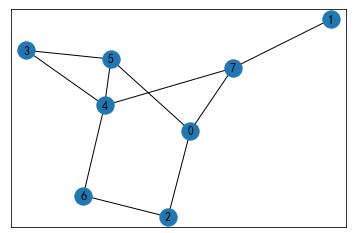
G = nx.Graph()根据定义,Graph是一组节点(顶点)和已识别的节点对(称为边、链接等)的集合。
1.1 清空图
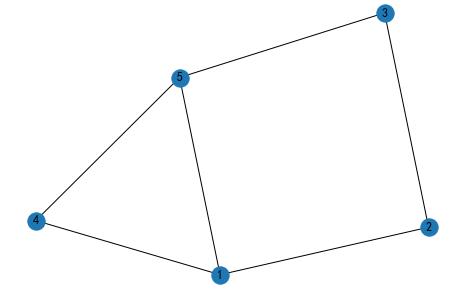
G.clear()1.2 从dataframe中导入图信息
import numpy as np
import pandas as pd
import networkx as nx
import matplotlib.pyplot as plt
edges=pd.DataFrame()
edges['sources']=[1,1,1,2,2,3,3,4,4,5,5,5]
#有向边的起点
edges['targets']=[2,4,5,3,1,2,5,1,5,1,3,4]
#有向边的终点
edges['weights']=[1,1,1,1,1,1,1,2,1,1,1,1]
#各边的权重
G=nx.from_pandas_edgelist(
edges,
source='sources',
target='targets',
edge_attr='weights')
nx.draw(G, with_labels=True)
plt.show()2 节点
2.1 一次添加一个节点
G.add_node(1)2.2 从任何 iterable 容器(如列表)中添加节点
G.add_nodes_from([2, 3])2.3 从元组中添加节点和节点属性
G.add_nodes_from([
(4, {"color": "red"}),
(5, {"color": "green"}),
])2.4 合并图中一个节点到另一个图中
H = nx.Graph()
H.add_nodes_from(G)2.5 查看点的数量
G.number_of_nodes()2.6 删除点
G.remove_node(2)
G.remove_nodes_from({1,2])3 边
3.1 一次添加一条边
G.add_edge(1, 2)
#或者:
e = (2, 3)
G.add_edge(*e) # unpack edge tuple*3.2 添加边列表
G.add_edges_from([(1, 2), (1, 3)])3.3 从元组中添加边和边属性
G.add_edges_from([
(2, 3, {'weight': 3.1415})
])3.4 查看边的数量
G.number_of_edges()
3.5 删除边
G.remove_edge(1, 3)
G.remove_edges_from([(1, 2), (1, 3)])3.6 增加带权边
G.add_weighted_edges_from([(1, 2, 0.125), (1, 3, 0.75), (2, 4, 1.2), (3, 4, 0.375)])4 图的基本属性
一部分属性的具体介绍可以看GNN 笔记1 图的概念_刘文巾的博客-CSDN博客
4.1 节点集合
G = nx.Graph()
G.add_node(1)
G.add_nodes_from([2, 3])
G.add_edge(1, 2)
G.add_edges_from([(1, 3)])
print(list(G.nodes()))
#[1, 2, 3]4.2 边集合
G = nx.Graph()
G.add_node(1)
G.add_nodes_from([2,3])
G.add_edge(1, 2)
G.add_edges_from(
[(1, 3, {'weight': 3.1415})]
)
print(G.edges)
#[(1, 2), (1, 3)]
print(G.edges.data())
#[(1, 2, {}), (1, 3, {'weight': 3.1415})]
print(G.edges.data('weight'))
#[(1, 2, None), (1, 3, 3.1415)]4.2.1 可以用G[i][j]表示连接i和j的边的信息
G = nx.Graph()
G.add_node(1)
G.add_nodes_from([2,3])
G.add_edge(1, 2)
G.add_edges_from(
[(1, 3, {'weight': 3.1415})]
)
print(G[1][2],G[1][3],G[1][3]['weight'])
#{} {'weight': 3.1415} 3.14154.2.2 也可以用G.edges[i,j]表示连接i和j的边的信息
G = nx.Graph()
G.add_node(1)
G.add_nodes_from([2,3])
G.add_edge(1, 2)
G.add_edges_from(
[(1, 3, {'weight': 3.1415})]
)
print(G.edges[1,3],G.edges[1,3]['weight'])
#{'weight': 3.1415} 3.14154.3 点相邻的集合
G = nx.Graph()
G.add_node(1)
G.add_nodes_from([2, 3])
G.add_edge(1, 2)
G.add_edges_from([(1, 3)])
print(list(G.adj[1]))
#[2, 3]
#或
print(list(G.neighbors(1)))
#[2, 3]
#或
print(G[1])
#{2: {}, 3: {}}
#2和3大括号里面的是相连接的边的性质,我们这里没有设置
#或
print(G.adj)
#{1: {2: {}, 3: {}}, 2: {1: {}}, 3: {1: {}}}G = nx.Graph()
G.add_node(1)
G.add_nodes_from([2,3])
G.add_edge(1, 2)
G.add_edges_from(
[(1, 3, {'weight': 3.1415})]
)
print(G[1])
#{2: {}, 3: {'weight': 3.1415}}4.4 节点的度
G = nx.Graph()
G.add_node(1)
G.add_nodes_from([2, 3])
G.add_edge(1, 2)
G.add_edges_from([(1, 3)])
print(G.degree[1])
#2
print(G.degree([1,2]))
#[(1, 2), (2, 1)],表示点1的度为2,点2的度为1
print(nx.degree(G))
#[(1, 2), (2, 1), (3, 1)]
#G图所有点的度
#如果是加权边,也可以显示它的加权度(这里用到了后面第七节的多重图)
MG = nx.MultiGraph()
MG.add_weighted_edges_from([(1, 2, 0.5), (1, 2, 0.75), (2, 3, 0.5)])
print(MG.degree([1],weight='weight'))
#[(1, 1.25)]
4.5 点射出来的边
G = nx.Graph()
G.add_node(1)
G.add_nodes_from([2, 3])
G.add_edge(1, 2)
G.add_edges_from([(1, 3)])
print(G.edges([3,2]))
#[(3, 1), (2, 1)]4.6连通分量

G=nx.Graph()
G.add_edges_from([(1,2),(1,4),(1,5),(2,3),(3,5),(4,5)])
list(nx.connected_components(G))
#[{1, 2, 3, 4, 5}]4.7 图的直径
G=nx.Graph()
G.add_edges_from([(1,2),(1,4),(1,5),(2,3),(3,5),(4,5)])
nx.diameter(G)
#24.8 度中心性
G=nx.Graph()
G.add_edges_from([(1,2),(1,4),(1,5),(2,3),(3,5),(4,5)])
nx.degree_centrality(G)
#{1: 0.75, 2: 0.5, 4: 0.5, 5: 0.75, 3: 0.5}4.9 连接中心性
G=nx.Graph()
G.add_edges_from([(1,2),(1,4),(1,5),(2,3),(3,5),(4,5)])
nx.closeness_centrality(G)
#{1: 0.75, 2: 0.5, 4: 0.5, 5: 0.75, 3: 0.5}4.10 特征向量中心性
G=nx.Graph()
G.add_edges_from([(1,2),(1,4),(1,5),(2,3),(3,5),(4,5)])
nx.eigenvector_centrality(G)
'''
{1: 0.5298988890761731,
2: 0.35775191431708964,
4: 0.4271316779596084,
5: 0.5298988890761731,
3: 0.35775191431708964}
'''4.11 中介中心性
G=nx.Graph()
G.add_edges_from([(1,2),(1,4),(1,5),(2,3),(3,5),(4,5)])
nx.betweenness_centrality(G)
#{1: 0.25, 2: 0.08333333333333333, 4: 0.0, 5: 0.25, 3: 0.08333333333333333}5 向图形、节点和边添加属性
任何属性都可以附加到图形、节点或边上。
每个图、节点和边都可以在关联的属性字典中保存键/值属性对(键必须是可哈希的)。
默认情况下,这些属性为空,但我们可以使用 add_edge , add_node 或直接对属性字典 G.graph , G.nodes 和 G.edges 进行操作
5.1 图形属性
5.1.1 创建新图形时分配图形属性
G = nx.Graph(day="Friday")
G.graph
#{'day': 'Friday'}5.1.2 创建后修改属性
G.graph['day'] = "Monday"
G.graph
#{'day': 'Monday'}5.2 节点属性
添加节点属性 add_node() , add_nodes_from()
G.add_node(1, time='5pm')
G.add_nodes_from([3], time='2pm')修改节点属性 G.nodes
G.nodes[1]['room'] = 714
G.nodes.data()
#NodeDataView({1: {'time': '5pm', 'room': 714}, 3: {'time': '2pm'}})5.3 边缘属性
添加/更改边缘属性 add_edge() , add_edges_from()
G.add_edge(1, 2, weight=4.7 )
G.add_edges_from([(3, 4), (4, 5)], color='red')
#两条边color都是red
G.add_edges_from([(1, 2, {'color': 'blue'}), (2, 3, {'weight': 8})])使用下标符号
G[1][2]['weight'] = 4.7
G.edges[3, 4]['weight'] = 4.26 有向图
有向图用Digraph进行声明。前面无向图的大部分操作Digraph都可以使用。
在此基础上,Digraph还有:
6.1 出入度
DG = nx.DiGraph()
DG.add_weighted_edges_from([(1, 2, 0.5), (3, 1, 0.75)])
#添加加权边
print(DG.out_degree(1, weight='weight'))
#出度,如果写了 weight='weight',那么就是计算出度的权重
#0.5
print(DG.in_degree(1))
#出度,如果没有写 weight='weight',那么就是计算出度(射向几个点)
#16.2 指向的点和指向它的点
DG = nx.DiGraph()
DG.add_weighted_edges_from([(1, 2, 0.5), (3, 1, 0.75)])
print(list(DG.successors(1)))
#[2]
print(list(DG.predecessors(1)))
#[3]6.3 有向图无向图互转
6.3.1 有向图转无向图
有两种方法:
DG = nx.DiGraph()
DG.add_weighted_edges_from([(1, 2, 0.5), (3, 1, 0.75)])
DG
#直接pring(DG)不会有东西打印出来。
#在命令行里面敲下这些指令,然后出来这样的输出:
#<networkx.classes.digraph.DiGraph at 0x27a716f4a08>
#说明此时是有向图
G=DG.to_undirected()
G
#<networkx.classes.graph.Graph at 0x27a706601c8>
#此时已经是无向图了
#或者
G=nx.Graph(DG)
G
#<networkx.classes.graph.Graph at 0x27a71909cc8>
#此时也是无向图6.3.2 无向图转有向图
和有向图转无向图一样,也有两种方法:
DG = nx.Graph()
DG.add_weighted_edges_from([(1, 2, 0.5), (3, 1, 0.75)])
DG
#<networkx.classes.graph.Graph at 0x27a71b73108>
#此时是无向图
G=DG.to_directed()
G
#<networkx.classes.digraph.DiGraph at 0x27a71af7248>
#此时是有向图
G=nx.DiGraph(DG)
G
#<networkx.classes.digraph.DiGraph at 0x27a71892c48>
#有向图了
7 多重图
networkx也提供了多重图的实现。在两个点之间可能有多条边,每条边描述了一些属性。
多重图有向图和无向图都有,分别是MultiGraph 和MultiDiGraph
MG = nx.MultiGraph()
MG.add_weighted_edges_from([(1, 2, 0.5), (1, 2, 0.75), (2, 3, 0.5)])
dict(MG.degree(weight='weight'))
#{1: 1.25, 2: 1.75, 3: 0.5}有一点是需要注意的,多重图转回单边图的时候,两个点之间只会留下权重最大的一条边
G=nx.Graph(MG)
dict(G.degree(weight='weight'))
'''
{1: 0.75, 2: 1.25, 3: 0.5}
1<--->2 之间本来有两条边,现在只留下权重大的1.25
'''8 图的操作
8.1 子图
G = nx.Graph()
G.add_weighted_edges_from([(1, 5, 0.1),(5,2,0.1), (1, 4, 0.75), (2, 3, 0.5),(4,3,1)])
SG=nx.subgraph(G,[1,2,5])
#表示SG是由G的结构,[1,2,5]这几个点组成的子图
SG.edges.data('weight')
#EdgeDataView([(1, 5, 0.1), (5, 2, 0.1)])8.2 合并图
8.2.1 union
将两张图和并
G1 = nx.Graph()
G1.add_edges_from([(1, 5),(5,2), (1, 4), (2, 3),(4,3)])
print(G1.nodes)
#[1, 5, 2, 4, 3]
G2 = nx.Graph()
G2.add_edges_from([(11, 13)])#,(1,2), (1, 4), (2, 5),(4,3)])
print(G2.nodes)
#[11, 13]
UG=nx.union(G1,G2)
print(UG.nodes)
#[1, 5, 2, 4, 3, 11, 13]如果这两张图中有相同的点,那么会报错
G1 = nx.Graph()
G1.add_edges_from([(1, 5),(5,2), (1, 4), (2, 3),(4,3)])
G2 = nx.Graph()
G2.add_edges_from([(1,2), (1, 4), (2, 5),(4,3)])
UG=nx.union(G1,G2)
'''
NetworkXError: ('The node sets of G and H are not disjoint.',
'Use appropriate rename=(Gprefix,Hprefix)or use disjoint_union(G,H).')
'''8.2.2 disjoint_union
即使两张图中有相同的点,也不会报错,而是把相同的点重命名成新的点
import matplotlib.pyplot as plt
G1 = nx.Graph()
G1.add_edges_from([(1, 5),(5,2), (1, 4), (2, 3),(4,3)])
print(G1.nodes)
#[1, 5, 2, 4, 3]
G2 = nx.Graph()
G2.add_edges_from([(1,2), (1, 4), (2, 5),(6,3)])
print(G2.nodes)
#[1, 2, 4, 5, 6, 3]
UG=nx.disjoint_union(G1,G2)
print(UG.nodes)
#[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print(UG.edges)
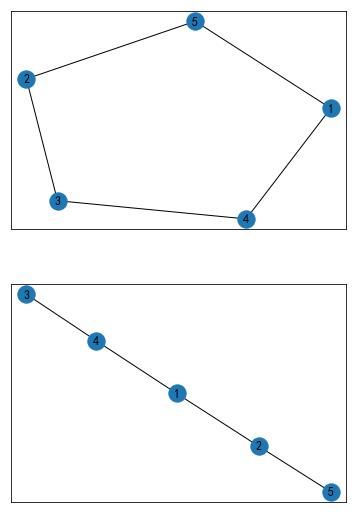
# 对点进行了重命名8.2.3 判断合并效果
import matplotlib.pyplot as plt
G1 = nx.Graph()
G1.add_edges_from([(1, 5),(5,2), (1, 4), (2, 3),(4,3)])
nx.draw_networkx(G1)
plt.show()
G2 = nx.Graph()
G2.add_edges_from([(1,2), (1, 4), (2, 5),(4,3)])
nx.draw_networkx(G2)
plt.show()
UG=nx.disjoint_union(G1,G2)
nx.draw_networkx(UG)
plt.show()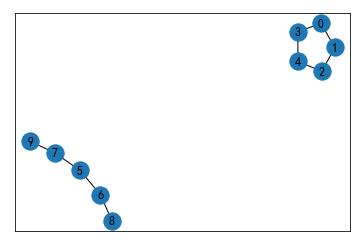
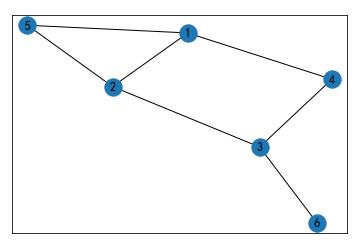
8.3 笛卡尔乘积
cartesian_product(G, H),G的每个点和H的每个点都需要有连接。
G1 = nx.Graph()
G1.add_edges_from([(1, 5),(5,2), (1, 4), (2, 3),(4,3)])
G2 = nx.Graph()
G2.add_edges_from([(1,2), (1, 4), (2, 5),(4,3)])
CG=nx.cartesian_product(G1,G2)
nx.draw_networkx(CG)
plt.show()8.4 图的叠加
compose(G, H) 就是G中的边保留,H中的边叠加到G上
此时如果H中有和G中名称相同的点,那么在compose函数中视为是一个点。
G1 = nx.Graph()
G1.add_edges_from([(1, 5),(5,2), (1, 4), (2, 3),(4,3)])
G2 = nx.Graph()
G2.add_edges_from([(1,2), (1, 4), (2, 5),(6,3)])
CG=nx.compose(G1, G2)
nx.draw_networkx(CG)
plt.show()原来G1中的五条边现在都在,然后G2中的(1,4),(2,5)就是原来G1中的边,剩下的两条边就是新加的边。
8.5 补图
complement (g)——返回g的补图
9 特殊的图
9.1 全连接图
complete_graph (n) n个点之间两两连接
G=nx.complete_graph(10)
nx.draw_networkx(G)
plt.show()9.2 二部图
G=nx.complete_bipartite_graph(3,3)
nx.draw_networkx(G)
plt.show() 
9.3 杠铃图
barbell_graph (M1,M2)
——M1表示杠铃两头全连接图的顶点数
——M2表示连接两个全连接图的路径中的节点数
G=nx.barbell_graph(5,4)
nx.draw_networkx(G)
plt.show() 
9.4 棒棒糖图
lollipop_graph (m,n)
——m,棒棒糖图头部全连接图的顶点数
——n,连接棒棒糖图头的路径的节点数
G=nx.lollipop_graph (5,4)
nx.draw_networkx(G)
plt.show()9.5 彼得森图
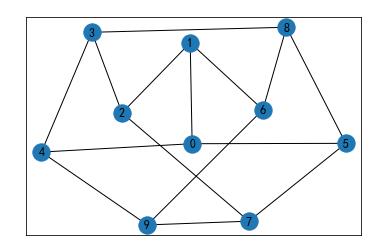
Petersen图一般译为彼得森图,是一个由10个顶点和15条边构成的连通简单图。
Petersen图的同构多种多样,形态各异,共120多种,然而它不是平面图,因而没有一种使得边与边没有交点。
G=nx.petersen_graph()
nx.draw_networkx(G)
plt.show()每次会显示一种彼得森图的同构形态(比如下面是连续两次plt.show()的结果)

9.6 塔特图
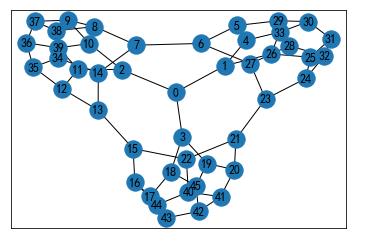
感谢评论区的大佬给出定义!
塔特图是具有46个顶点和69条边的3正则图。它的色数为4,色指数为3,周长为4,直径为8。
塔特图是一个三次多面体图,但是非哈密顿图。
因此,它是塔特猜想的一个反例(即每个三正多面体都有一个哈密顿环)。
G=nx.tutte_graph()
nx.draw_networkx(G)
plt.show()这个图也有很多的异构型,比如下面是连续的两个plt.show()的结果
9.7 小迷宫
返回一个带有循环的小迷宫
G=nx.sedgewick_maze_graph()
nx.draw_networkx(G)
plt.show()9.8 3-正则柏拉图四面体
G=nx.tetrahedral_graph()
nx.draw_networkx(G)
plt.show()10 图的应用
10.1 最短路径
G = nx.Graph()
G.add_weighted_edges_from([(1, 5, 0.1),(5,2,0.1), (1, 4, 0.75), (2, 3, 0.5),(4,3,1)]
nx.shortest_path(G,1,3)
'''
找点1到点3的最短路径,但此时是不考虑weight的
只考虑1到3经过的点最少
所以此时会返回[1, 4, 3]
'''
nx.shortest_path_length(G,1,3)
'''
返回点1到点3的最短路径包括几条边
同样此时是不考虑weight的,只考虑1到3经过的点最少
所以此时会返回2
'''
nx.shortest_path(G,1,3,weight='weight')
'''
此时考虑权重了
1->5->2->3的路径长度是小于1->4->3的
所以此时会返回[1, 5, 2, 3]
'''
nx.shortest_path_length(G,1,3,weight='weight')
'''
此时考虑权重了
1->5->2->3的路径长度是小于1->4->3的
所以此时会返回0.7
'''
dict(nx.all_pairs_shortest_path(G))
##每一对点之间的最小路径
'''
{1: {1: [1], 5: [1, 5], 4: [1, 4], 2: [1, 5, 2], 3: [1, 4, 3]},
5: {5: [5], 1: [5, 1], 2: [5, 2], 4: [5, 1, 4], 3: [5, 2, 3]},
2: {2: [2], 5: [2, 5], 3: [2, 3], 1: [2, 5, 1], 4: [2, 3, 4]},
4: {4: [4], 1: [4, 1], 3: [4, 3], 5: [4, 1, 5], 2: [4, 3, 2]},
3: {3: [3], 2: [3, 2], 4: [3, 4], 5: [3, 2, 5], 1: [3, 4, 1]}}
'''
dict(nx.all_pairs_shortest_path_length(G))
#每一对之间的最小路径的长度
'''
{1: {1: 0, 4: 1, 5: 1, 2: 2, 3: 2},
5: {5: 0, 1: 1, 2: 1, 3: 2, 4: 2},
2: {2: 0, 3: 1, 5: 1, 1: 2, 4: 2},
4: {4: 0, 1: 1, 3: 1, 2: 2, 5: 2},
3: {3: 0, 2: 1, 4: 1, 1: 2, 5: 2}}
'''
11 绘图
import matplotlib.pyplot as plt
G = nx.Graph()
G.add_weighted_edges_from([(1, 5, 0.1),(5,2,0.1), (1, 4, 0.75), (2, 3, 0.5),(4,3,1)])
nx.draw(G, with_labels=True, font_weight='bold')
#with_labels=False的话,图中的点点中是没有数值的
plt.show()
plt.savefig("path.png")
#保存图片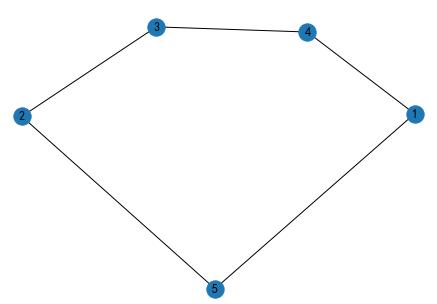
以上是关于python库整理:networkx 包的主要内容,如果未能解决你的问题,请参考以下文章